Overview of Adaptive Filters and Applications
Adaptive filters are digital filters whose coefficients change with an objective to make the filter converge to an optimal state. The optimization criterion is a cost function, which is most commonly the mean square of the error signal between the output of the adaptive filter and the desired signal. As the filter adapts its coefficients, the mean square error (MSE) converges to its minimal value. At this state, the filter is adapted and the coefficients have converged to a solution. The filter output, y(k), is then said to match very closely to the desired signal, d(k). When you change the input data characteristics, sometimes called filter environment, the filter adapts to the new environment by generating a new set of coefficients for the new data.
General Adaptive Filter Algorithm

Adaptive Filters in DSP System Toolbox
Least Mean Squares (LMS) Based FIR Adaptive Filters
Adaptive Filter Object | Adapting Algorithm |
|---|---|
Block LMS FIR adaptive filter algorithm | |
Filtered-x LMS FIR adaptive filter algorithm | |
LMS FIR adaptive filter algorithm Normalized LMS FIR adaptive filter algorithm Sign-data LMS FIR adaptive filter algorithm Sign-error LMS FIR adaptive filter algorithm Sign-sign LMS FIR adaptive filter algorithm |
Adaptive Filter Block | Adapting Algorithm |
|---|---|
Block LMS FIR adaptive filter algorithm | |
Block LMS FIR adaptive filter algorithm in frequency domain | |
LMS FIR adaptive filter algorithm Normalized LMS FIR adaptive filter algorithm Sign-data LMS FIR adaptive filter algorithm Sign-error LMS FIR adaptive filter algorithm Sign-sign LMS FIR adaptive filter algorithm | |
| LMS Update | LMS FIR weight update algorithm Normalized LMS FIR weight update algorithm Sign-data LMS FIR weight update algorithm Sign-error LMS FIR weight update algorithm Sign-sign LMS FIR weight update algorithm |
Recursive Least Squares (RLS) Based FIR Adaptive Filters
Adaptive Filter Object | Adapting Algorithm |
|---|---|
Fast transversal least-squares adaptation algorithm Sliding window FTF adaptation algorithm | |
QR-decomposition RLS adaptation algorithm Householder RLS adaptation algorithm Householder SWRLS adaptation algorithm Recursive-least squares (RLS) adaptation algorithm Sliding window (SW) RLS adaptation algorithm |
Adaptive Filter Block | Adapting Algorithm |
|---|---|
Exponentially weighted recursive least-squares (RLS) algorithm |
Affine Projection (AP) FIR Adaptive Filters
Adaptive Filter Object | Adapting Algorithm |
|---|---|
Affine projection algorithm that uses direct matrix inversion Affine projection algorithm that uses recursive matrix updating Block affine projection adaptation algorithm |
FIR Adaptive Filters in the Frequency Domain (FD)
Adaptive Filter Object | Adapting Algorithm |
|---|---|
Constrained frequency domain adaptation algorithm Unconstrained frequency domain adaptation algorithm Partitioned and constrained frequency domain adaptation algorithm Partitioned and unconstrained frequency domain adaptation algorithm |
Adaptive Filter Block | Adapting Algorithm |
|---|---|
Constrained frequency domain adaptation algorithm Unconstrained frequency domain adaptation algorithm Partitioned and constrained frequency domain adaptation algorithm Partitioned and unconstrained frequency domain adaptation algorithm |
Lattice-Based (L) FIR Adaptive Filters
Adaptive Filter Object | Adapting Algorithm |
|---|---|
Gradient adaptive lattice filter adaptation algorithm Least squares lattice adaptation algorithm QR decomposition RLS adaptation algorithm |
For more information on these algorithms, refer to the algorithm section of the respective reference pages. Full descriptions of the theory appear in the adaptive filter references [1] and [2].
Choosing an Adaptive Filter
At steady state when the filter has adapted, the error between the filter output and the desired signal is minimal, not zero. This error is known as the steady state error. The speed with which the filter converges to the optimal state, known as the convergence speed, depends on multiple factors such nature of the input signal, choice of the adaptive filter algorithm, and step size of the algorithm. The choice of the filter algorithm usually depends factors such as convergence performance required for the application, computational complexity of the algorithm, filter stability in the environment, and any other constraints.
LMS algorithm is simple to implement, but has stability issues. The normalized version of the LMS algorithm comes with improved convergence speed, more stability, but has increased computational complexity. For an example that compares the two, see Compare Convergence Performance Between LMS Algorithm and Normalized LMS Algorithm. RLS algorithms are highly stable, do very well in time-varying environments, but are computationally more complex than the LMS algorithms. For a comparison, see Compare RLS and LMS Adaptive Filter Algorithms. Affine projection filters do well when the input is colored and have a very good convergence performance. Adaptive lattice filters provide good convergence but come with increased computational cost. The choice of the algorithm depends on the environment and the specifics of the application.
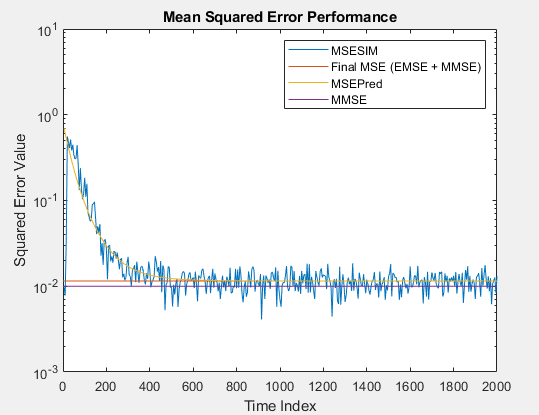
Mean Squared Error Performance
Minimizing the mean square of the error signal between the output of the adaptive
filter and the desired signal is the most common optimization criterion for adaptive
filters. The actual MSE (MSESIM) of the adaptive filter you are implementing can be
determined using the msesim
function. The trajectory of this MSE is expected to follow that of the predicted MSE
(MSEPred), which is computed using the msepred
function. The minimum mean square error (MMSE) is estimated by the msepred
function using a Wiener filter. The Weiner filter minimizes the mean squared error
between the desired signal and the input signal filtered by the Wiener filter. A
large value of the mean squared error indicates that the adaptive filter cannot
accurately track the desired signal. The minimal value of the mean squared error
ensures that the adaptive filter is optimal. The excess mean square error (EMSE),
determined by the msepred function, is the difference between
the MSE introduced by the adaptive filters and the MMSE produced by the
corresponding Wiener filter. The final MSE shown below is the sum of EMSE and MMSE,
and equals the predicted MSE after convergence.
Common Applications
System Identification –– Using an Adaptive Filter to Identify an Unknown System
One common adaptive filter application is to use adaptive filters to identify an unknown system, such as the response of an unknown communications channel or the frequency response of an auditorium, to pick fairly divergent applications. Other applications include echo cancellation and channel identification.
In the figure, the unknown system is placed in parallel with the adaptive filter. This layout represents just one of many possible structures. The shaded area contains the adaptive filter system.

Clearly, when e(k) is very small, the adaptive filter response is close to the response of the unknown system. In this case, the same input feeds both the adaptive filter and the unknown. If, for example, the unknown system is a modem, the input often represents white noise, and is a part of the sound you hear from your modem when you log in to your Internet service provider.
Inverse System Identification –– Determining an Inverse Response to an Unknown System
By placing the unknown system in series with your adaptive filter, your filter adapts to become the inverse of the unknown system as e(k) becomes very small. As shown in the figure, the process requires a delay inserted in the desired signal d(k) path to keep the data at the summation synchronized. Adding the delay keeps the system causal.

Including the delay to account for the delay caused by the unknown system prevents this condition.
Plain old telephone systems (POTS) commonly use inverse system identification to compensate for the copper transmission medium. When you send data or voice over telephone lines, the copper wires behave like a filter, having a response that rolls off at higher frequencies (or data rates) and having other anomalies as well.
Adding an adaptive filter that has a response that is the inverse of the wire response, and configuring the filter to adapt in real time, lets the filter compensate for the rolloff and anomalies, increasing the available frequency output range and data rate for the telephone system.
Noise or Interference Cancellation –– Using an Adaptive Filter to Remove Noise from an Unknown System
In noise cancellation, adaptive filters let you remove noise from a signal in real time. Here, the desired signal, the one to clean up, combines noise and desired information. To remove the noise, feed a signal n'(k) to the adaptive filter that is correlated to the noise to be removed from the desired signal.

So long as the input noise to the filter remains correlated to the unwanted noise accompanying the desired signal, the adaptive filter adjusts its coefficients to reduce the value of the difference between y(k) and d(k), removing the noise and resulting in a clean signal in e(k). Notice that in this application, the error signal actually converges to the input data signal, rather than converging to zero.
Prediction –– Predicting Future Values of a Periodic Signal
Predicting signals requires that you make some key assumptions. Assume that the signal is either steady or slowly varying over time, and periodic over time as well.
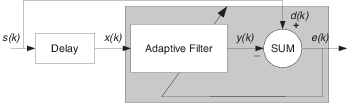
Accepting these assumptions, the adaptive filter must predict the future values of the desired signal based on past values. When s(k) is periodic and the filter is long enough to remember previous values, this structure with the delay in the input signal, can perform the prediction. You might use this structure to remove a periodic signal from stochastic noise signals.
Finally, notice that most systems of interest contain elements of more than one of the four adaptive filter structures. Carefully reviewing the real structure may be required to determine what the adaptive filter is adapting to.
Also, for clarity in the figures, the analog-to-digital (A/D) and digital-to-analog (D/A) components do not appear. Since the adaptive filters are assumed to be digital in nature, and many of the problems produce analog data, converting the input signals to and from the analog domain is probably necessary.
References
[1] Hayes, Monson H., Statistical Digital Signal Processing and Modeling. Hoboken, NJ: John Wiley & Sons, 1996, pp.493–552.
[2] Haykin, Simon, Adaptive Filter Theory. Upper Saddle River, NJ: Prentice-Hall, Inc., 1996.