polyshape
2-D polygonal shapes
Description
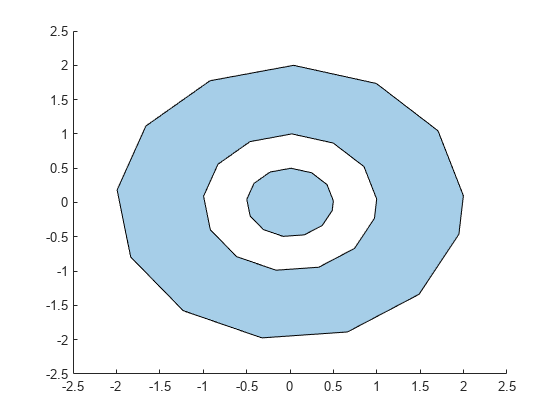
The polyshape function creates polygon-like shapes from 2-D
vertices. However, unlike polygons, a polyshape can have
discontiguous regions and holes. The properties of a polyshape object
describe its vertices, solid regions, and holes.
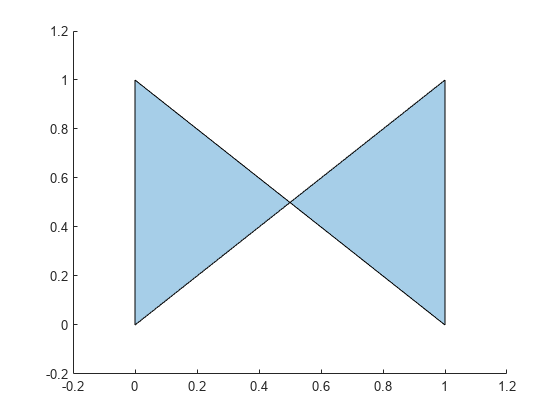
For example, pgon = polyshape([0 0 1 1],[1 0 0 1]) creates the
solid square defined by the four points (0,1), (0,0), (1,0), and (1,1).
>> pgon = polyshape([0 0 1 1],[1 0 0 1])
pgon =
polyshape with properties:
Vertices: [4×2 double]
NumRegions: 1
NumHoles: 0>> plot(pgon)

Creation
When creating a polyshape object, the input vertices should define
one or more boundaries of a polygon that have no intersections and are properly nested.
Otherwise, the polyshape function automatically alters the input
vertices as needed to create a well-defined polygon.
If you want to create a regular polygon, you can also use the nsidedpoly function. nsidedpoly enables you to
optionally specify parameters such as the center point and side length of the
polygon.
Syntax
Description
pgon = polyshape() creates an empty
polyshape object.
pgon = polyshape( creates a
P)polyshape from the 2-D vertices defined in the
N-by-2 matrix P, where
N is the number of vertices. The first column of
P defines the x-coordinates, and the
second column defines the y-coordinates.
pgon = polyshape(___,
specifies additional parameters for creating a Name,Value)polyshape
object for any of the previous syntaxes.