fitrnet
Syntax
Description
Use fitrnet to train a neural network for regression, such as
a feedforward, fully connected network. In a feedforward, fully connected network, the first
fully connected layer has a connection from the network input (predictor data), and each
subsequent layer has a connection from the previous layer. Each fully connected layer
multiplies the input by a weight matrix and then adds a bias vector. An activation function
follows each fully connected layer, excluding the last. The final fully connected layer
produces the network's output, namely predicted response values. For more information, see
Neural Network Structure.
Mdl = fitrnet(Tbl,ResponseVarName)Mdl trained using the
predictors in the table Tbl and the response values in the
ResponseVarName table variable.
You can use an array
ResponseVarName to specify multiple response variables. (since R2024b)
Mdl = fitrnet(Tbl,formula)Tbl. The input argument formula is an
explanatory model of the response and a subset of the predictor variables in
Tbl used to fit Mdl.
You can use formula to
specify multiple response variables. (since R2024b)
Mdl = fitrnet(___,Name=Value)LayerSizes and Activations name-value
arguments.
Convergence control, cross-validation, and hyperparameter optimization options are not supported for multiresponse regression.
[
also returns Mdl,AggregateOptimizationResults] = fitrnet(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments. You must
also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this syntax to
optimize on compact model size instead of cross-validation loss, and to perform a set of
multiple optimization problems that have the same options but different constraint
bounds.
Hyperparameter optimization options are not supported for multiresponse regression.
Examples
Train a neural network regression model, and assess the performance of the model on a test set.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Displacement,Horsepower, ... Model_Year,Origin,Weight,MPG);
Remove rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.20); trainingIdx = training(c); % Training set indices carsTrain = cars(trainingIdx,:); testIdx = test(c); % Test set indices carsTest = cars(testIdx,:);
Train a neural network regression model by passing the carsTrain training data to the fitrnet function. For better results, specify to standardize the predictor data.
Mdl = fitrnet(carsTrain,"MPG","Standardize",true)
Mdl =
RegressionNeuralNetwork
PredictorNames: {'Acceleration' 'Displacement' 'Horsepower' 'Model_Year' 'Origin' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: 5
ResponseTransform: 'none'
NumObservations: 314
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Mdl is a trained RegressionNeuralNetwork model. You can use dot notation to access the properties of Mdl. For example, you can specify Mdl.TrainingHistory to get more information about the training history of the neural network model.
Evaluate the performance of the regression model on the test set by computing the test mean squared error (MSE). Smaller MSE values indicate better performance.
testMSE = loss(Mdl,carsTest,"MPG")testMSE = 6.8780
Configure the fully connected layers of the neural network.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Cylinders, and so on. Store the response variable MPG in the variable Y.
load carbig
X = [Acceleration Cylinders Displacement Weight];
Y = MPG;Delete rows of X and Y where either array has missing values.
R = rmmissing([X Y]); X = R(:,1:end-1); Y = R(:,end);
Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.
rng("default") % For reproducibility of the partition c = cvpartition(length(Y),"Holdout",0.20); trainingIdx = training(c); % Indices for the training set XTrain = X(trainingIdx,:); YTrain = Y(trainingIdx); testIdx = test(c); % Indices for the test set XTest = X(testIdx,:); YTest = Y(testIdx);
Train a neural network regression model. Specify to standardize the predictor data, and to have 30 outputs in the first fully connected layer and 10 outputs in the second fully connected layer. By default, both layers use a rectified linear unit (ReLU) activation function. You can change the activation functions for the fully connected layers by using the Activations name-value argument.
Mdl = fitrnet(XTrain,YTrain,"Standardize",true, ... "LayerSizes",[30 10])
Mdl =
RegressionNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 319
LayerSizes: [30 10]
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Access the weights and biases for the fully connected layers of the trained model by using the LayerWeights and LayerBiases properties of Mdl. The first two elements of each property correspond to the values for the first two fully connected layers, and the third element corresponds to the values for the final fully connected layer for regression. For example, display the weights and biases for the first fully connected layer.
Mdl.LayerWeights{1}ans = 30×4
0.0123 0.0117 -0.0094 0.1175
-0.4081 -0.7849 -0.7201 -2.1720
0.6041 0.1680 -2.3952 0.0934
-3.2332 -2.8360 -1.8264 -1.5723
0.5851 1.5370 1.4623 0.6742
-0.2106 1.2830 -1.7489 -1.5556
0.4800 0.1012 -1.0044 -0.7959
1.8015 -0.5272 -0.7670 0.7496
-1.1428 -0.9902 0.2436 1.2288
-0.0833 -2.4265 0.8388 1.8597
0.1069 -0.6754 -2.4190 -2.1763
-0.4008 1.1705 2.0588 0.2282
0.6358 -0.4830 -1.6925 -1.1925
-0.9572 -1.2231 1.1647 1.0479
-0.5559 -0.0917 -3.6854 1.2579
⋮
Mdl.LayerBiases{1}ans = 30×1
-0.4450
-0.8751
-0.3872
-1.1345
0.4499
-2.1555
2.2111
1.2040
-1.4595
0.4639
-1.5912
-0.5617
0.6513
-2.0560
-2.2856
⋮
The final fully connected layer has one output. The number of layer outputs corresponds to the first dimension of the layer weights and layer biases.
size(Mdl.LayerWeights{end})ans = 1×2
1 10
size(Mdl.LayerBiases{end})ans = 1×2
1 1
To estimate the performance of the trained model, compute the test set mean squared error (MSE) for Mdl. Smaller MSE values indicate better performance.
testMSE = loss(Mdl,XTest,YTest)
testMSE = 18.3681
Compare the predicted test set response values to the true response values. Plot the predicted miles per gallon (MPG) along the vertical axis and the true MPG along the horizontal axis. Points on the reference line indicate correct predictions. A good model produces predictions that are scattered near the line.
testPredictions = predict(Mdl,XTest); plot(YTest,testPredictions,".") hold on plot(YTest,YTest) hold off xlabel("True MPG") ylabel("Predicted MPG")
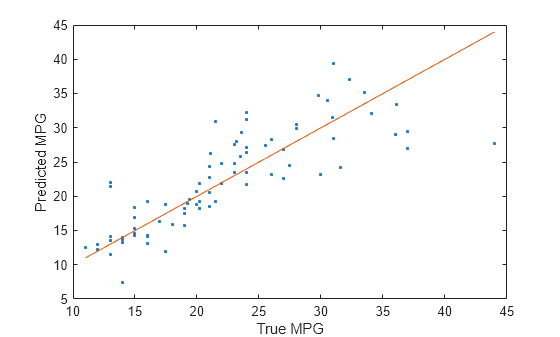
Since R2025a
Specify a custom neural network architecture using Deep Learning Toolbox™.
To specify a neural network of fully connected layers connected in series, use arguments like the LayerSizes argument to configure the neural network architecture. For neural networks with more complex architecture (such as, neural networks with skip connections), you can specify the architecture using the Network name-value argument with a dlnetwork object.
Load the carbig data set.
load carbig
X = [Acceleration Cylinders Displacement Weight];
Y = MPG;Delete rows of the data where either array has missing values.
R = rmmissing([X Y]); X = R(:,1:end-1); Y = R(:,end);
Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.
rng("default") % For reproducibility of the partition c = cvpartition(length(Y),Holdout=0.2); trainingIdx = training(c); % Indices for the training set XTrain = X(trainingIdx,:); YTrain = Y(trainingIdx); testIdx = test(c); % Indices for the test set XTest = X(testIdx,:); YTest = Y(testIdx);
Define a neural network architecture with these characteristics:
A feature input layer with an input size that matches the number of predictors.
Three fully connected layers followed by ReLU layers, connected in series, where the fully connected layers have output sizes of 12, and addition layers after the second and third fully connected layers.
Skip connections around the second and third fully connected layers using the addition layers.
A final fully connected layer with an output size that matches the number of responses.
inputSize = size(XTrain,2);
outputSize = size(YTrain,2);
net = dlnetwork;
layers = [
featureInputLayer(inputSize)
fullyConnectedLayer(12)
reluLayer(Name="relu1")
fullyConnectedLayer(12)
additionLayer(2,Name="add2")
reluLayer(Name="relu2")
fullyConnectedLayer(12)
additionLayer(2,Name="add3")
reluLayer
fullyConnectedLayer(outputSize)];
net = addLayers(net,layers);
net = connectLayers(net,"relu1","add2/in2");
net = connectLayers(net,"relu2","add3/in2");Visualize the neural network architecture in a plot.
figure plot(net)

Train a neural network regression model.
Mdl = fitrnet(XTrain,YTrain,Network=net,Standardize=true)
Mdl =
RegressionNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 319
LayerSizes: []
Activations: ''
OutputLayerActivation: ''
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×5 table]
View network information using dlnetwork.
Properties, Methods
Evaluate the performance of the regression model on the test set by computing the test mean squared error (MSE). Smaller values indicate better predictive accuracy.
testMSE = loss(Mdl,XTest,YTest)
testMSE = 14.3926
At each iteration of the training process, compute the validation loss of the neural network. Stop the training process early if the validation loss reaches a reasonable minimum.
Load the patients data set. Create a table from the data set. Each row corresponds to one patient, and each column corresponds to a diagnostic variable. Use the Systolic variable as the response variable, and the rest of the variables as predictors.
load patients
tbl = table(Age,Diastolic,Gender,Height,Smoker,Weight,Systolic);Separate the data into a training set tblTrain and a validation set tblValidation. The software reserves approximately 30% of the observations for the validation data set and uses the rest of the observations for the training data set.
rng("default") % For reproducibility of the partition c = cvpartition(size(tbl,1),"Holdout",0.30); trainingIndices = training(c); validationIndices = test(c); tblTrain = tbl(trainingIndices,:); tblValidation = tbl(validationIndices,:);
Train a neural network regression model by using the training set. Specify the Systolic column of tblTrain as the response variable. Evaluate the model at each iteration by using the validation set. Specify to display the training information at each iteration by using the Verbose name-value argument. By default, the training process ends early if the validation loss is greater than or equal to the minimum validation loss computed so far, six times in a row. To change the number of times the validation loss is allowed to be greater than or equal to the minimum, specify the ValidationPatience name-value argument.
Mdl = fitrnet(tblTrain,"Systolic", ... "ValidationData",tblValidation, ... "Verbose",1);
|==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 1| 516.021993| 3220.880047| 0.644473| 0.010948| 568.289202| 0| | 2| 313.056754| 229.931405| 0.067026| 0.005069| 304.023695| 0| | 3| 308.461807| 277.166516| 0.011122| 0.001717| 296.935608| 0| | 4| 262.492770| 844.627934| 0.143022| 0.000314| 240.559640| 0| | 5| 169.558740| 1131.714363| 0.336463| 0.000300| 152.531663| 0| | 6| 89.134368| 362.084104| 0.382677| 0.000634| 83.147478| 0| | 7| 83.309729| 994.830303| 0.199923| 0.000306| 76.634122| 0| | 8| 70.731524| 327.637362| 0.041366| 0.000309| 66.421750| 0| | 9| 66.650091| 124.369963| 0.125232| 0.000297| 65.914063| 0| | 10| 66.404753| 36.699328| 0.016768| 0.000360| 65.357335| 0| |==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 11| 66.357143| 46.712988| 0.009405| 0.000961| 65.306106| 0| | 12| 66.268225| 54.079264| 0.007953| 0.001245| 65.234391| 0| | 13| 65.788550| 99.453225| 0.030942| 0.000318| 64.869708| 0| | 14| 64.821095| 186.344649| 0.048078| 0.000321| 64.191533| 0| | 15| 62.353896| 319.273873| 0.107160| 0.000320| 62.618374| 0| | 16| 57.836593| 447.826470| 0.184985| 0.000314| 60.087065| 0| | 17| 51.188884| 524.631067| 0.253062| 0.000300| 56.646294| 0| | 18| 41.755601| 189.072516| 0.318515| 0.000318| 49.046823| 0| | 19| 37.539854| 78.602559| 0.382284| 0.000403| 44.633562| 0| | 20| 36.845322| 151.837884| 0.211286| 0.000304| 47.291367| 1| |==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 21| 36.218289| 62.826818| 0.142748| 0.000293| 46.139104| 2| | 22| 35.776921| 53.606315| 0.215188| 0.000367| 46.170460| 3| | 23| 35.729085| 24.400342| 0.060096| 0.001125| 45.318023| 4| | 24| 35.622031| 9.602277| 0.121153| 0.000321| 45.791861| 5| | 25| 35.573317| 10.735070| 0.126854| 0.000347| 46.062826| 6| |==========================================================================================|
Create a plot that compares the training mean squared error (MSE) and the validation MSE at each iteration. By default, fitrnet stores the loss information inside the TrainingHistory property of the object Mdl. You can access this information by using dot notation.
iteration = Mdl.TrainingHistory.Iteration; trainLosses = Mdl.TrainingHistory.TrainingLoss; valLosses = Mdl.TrainingHistory.ValidationLoss; plot(iteration,trainLosses,iteration,valLosses) legend(["Training","Validation"]) xlabel("Iteration") ylabel("Mean Squared Error")

Check the iteration that corresponds to the minimum validation MSE. The final returned model Mdl is the model trained at this iteration.
[~,minIdx] = min(valLosses); iteration(minIdx)
ans = 19
Assess the cross-validation loss of neural network models with different regularization strengths, and choose the regularization strength corresponding to the best performing model.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Displacement,Horsepower, ... Model_Year,Origin,Weight,MPG);
Delete rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan", ... "Germany","Sweden","Italy","England"],"NotUSA");
Create a cvpartition object for 5-fold cross-validation. cvp partitions the data into five folds, where each fold has roughly the same number of observations. Set the random seed to the default value for reproducibility of the partition.
rng("default") n = size(cars,1); cvp = cvpartition(n,"KFold",5);
Compute the cross-validation mean squared error (MSE) for neural network regression models with different regularization strengths. Try regularization strengths on the order of 1/n, where n is the number of observations. Specify to standardize the data before training the neural network models.
1/n
ans = 0.0026
lambda = (0:0.5:5)*1e-3; cvloss = zeros(length(lambda),1); for i = 1:length(lambda) cvMdl = fitrnet(cars,"MPG","Lambda",lambda(i), ... "CVPartition",cvp,"Standardize",true); cvloss(i) = kfoldLoss(cvMdl); end
Plot the results. Find the regularization strength corresponding to the lowest cross-validation MSE.
plot(lambda,cvloss) xlabel("Regularization Strength") ylabel("Cross-Validation Loss")

[~,idx] = min(cvloss); bestLambda = lambda(idx)
bestLambda = 0.0045
Train a neural network regression model using the bestLambda regularization strength.
Mdl = fitrnet(cars,"MPG","Lambda",bestLambda, ... "Standardize",true)
Mdl =
RegressionNeuralNetwork
PredictorNames: {'Acceleration' 'Displacement' 'Horsepower' 'Model_Year' 'Origin' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: 5
ResponseTransform: 'none'
NumObservations: 392
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [761×7 table]
Properties, Methods
Create a neural network with low error by using the OptimizeHyperparameters argument. This argument causes fitrnet to minimize cross-validation loss over some problem hyperparameters by using Bayesian optimization.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Displacement,Horsepower, ... Model_Year,Origin,Weight,MPG);
Delete rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.20); trainingIdx = training(c); % Training set indices carsTrain = cars(trainingIdx,:); testIdx = test(c); % Test set indices carsTest = cars(testIdx,:);
Train a regression neural network using the OptimizeHyperparameters argument set to "auto". For reproducibility, set the AcquisitionFunctionName to "expected-improvement-plus" in a HyperparameterOptimizationOptions structure. fitrnet performs Bayesian optimization by default. To use grid search or random search, set the Optimizer field in HyperparameterOptimizationOptions.
rng("default") % For reproducibility Mdl = fitrnet(carsTrain,"MPG","OptimizeHyperparameters","auto", ... "HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus"))
|============================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 1 | Best | 2.223 | 9.231 | 2.223 | 2.223 | relu | true | 3.841 | [101 47 15] |
| 2 | Accept | 3.0797 | 6.4178 | 2.223 | 2.2571 | sigmoid | false | 7.5401e-07 | [100 17] |
| 3 | Best | 2.1171 | 2.4398 | 2.1171 | 2.1312 | relu | true | 0.01569 | 15 |
| 4 | Accept | 2.5142 | 4.2068 | 2.1171 | 2.1326 | none | true | 0.00016461 | [ 2 145 8] |
| 5 | Accept | 3.0246 | 0.26994 | 2.1171 | 2.1172 | relu | true | 5.4264e-08 | 1 |
| 6 | Accept | 2.9859 | 0.77249 | 2.1171 | 2.171 | relu | true | 0.1243 | [ 5 1] |
| 7 | Accept | 2.14 | 2.5549 | 2.1171 | 2.1173 | relu | true | 0.0082696 | 17 |
| 8 | Accept | 2.7596 | 0.41156 | 2.1171 | 2.1173 | relu | true | 5.8567 | 72 |
| 9 | Accept | 3.0702 | 6.3673 | 2.1171 | 2.1173 | relu | true | 4.4611e-07 | [ 77 24 12] |
| 10 | Accept | 2.2126 | 1.8954 | 2.1171 | 2.1177 | relu | true | 4.1722e-07 | 9 |
| 11 | Accept | 2.9998 | 16.958 | 2.1171 | 2.1177 | relu | true | 0.00088575 | [250 47 63] |
| 12 | Accept | 3.3504 | 11.524 | 2.1171 | 2.1173 | relu | true | 1.2716e-06 | [103 55 15] |
| 13 | Accept | 2.223 | 1.7197 | 2.1171 | 2.1174 | relu | true | 0.0003368 | 10 |
| 14 | Accept | 6.4098 | 0.22799 | 2.1171 | 2.1301 | relu | true | 251.71 | [ 67 34 275] |
| 15 | Accept | 6.412 | 0.12626 | 2.1171 | 2.1175 | relu | true | 298.04 | [ 30 23 10] |
| 16 | Accept | 2.1882 | 1.6043 | 2.1171 | 2.1176 | relu | true | 5.2998e-05 | 6 |
| 17 | Accept | 2.5141 | 0.46234 | 2.1171 | 2.1176 | none | true | 0.0031007 | 4 |
| 18 | Accept | 2.5139 | 2.2299 | 2.1171 | 2.1176 | none | true | 0.07401 | [ 33 16 83] |
| 19 | Accept | 2.5756 | 0.10945 | 2.1171 | 2.1173 | none | true | 1.6796 | 2 |
| 20 | Best | 2.0906 | 8.1833 | 2.0906 | 2.0906 | relu | true | 0.58373 | [ 13 58 65] |
|============================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 21 | Accept | 2.4488 | 2.5839 | 2.0906 | 2.091 | relu | true | 3.4514e-06 | 26 |
| 22 | Accept | 2.5142 | 3.9131 | 2.0906 | 2.091 | none | true | 3.9367e-06 | 255 |
| 23 | Accept | 2.5142 | 0.21115 | 2.0906 | 2.0909 | none | true | 9.1909e-08 | [ 27 12 14] |
| 24 | Accept | 6.3852 | 0.32065 | 2.0906 | 2.0908 | none | true | 91.409 | [ 27 193 71] |
| 25 | Accept | 2.5312 | 15.695 | 2.0906 | 2.0908 | sigmoid | false | 0.00062 | [165 66] |
| 26 | Accept | 2.588 | 4.0838 | 2.0906 | 2.0908 | sigmoid | false | 0.035987 | 100 |
| 27 | Accept | 3.9253 | 6.7469 | 2.0906 | 2.0908 | sigmoid | false | 3.0045 | [ 5 296] |
| 28 | Accept | 2.1903 | 8.4032 | 2.0906 | 2.0911 | relu | true | 1.1661 | [ 3 300 232] |
| 29 | Accept | 2.5142 | 2.5771 | 2.0906 | 2.0912 | none | true | 1.636e-06 | [ 1 294 27] |
| 30 | Accept | 2.1336 | 6.7976 | 2.0906 | 2.0911 | relu | true | 0.039606 | [ 4 299] |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 138.7963 seconds
Total objective function evaluation time: 129.0442
Best observed feasible point:
Activations Standardize Lambda LayerSizes
___________ ___________ _______ ______________
relu true 0.58373 13 58 65
Observed objective function value = 2.0906
Estimated objective function value = 2.0911
Function evaluation time = 8.1833
Best estimated feasible point (according to models):
Activations Standardize Lambda LayerSizes
___________ ___________ _______ ______________
relu true 0.58373 13 58 65
Estimated objective function value = 2.0911
Estimated function evaluation time = 8.1846

Mdl =
RegressionNeuralNetwork
PredictorNames: {'Acceleration' 'Displacement' 'Horsepower' 'Model_Year' 'Origin' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: 5
ResponseTransform: 'none'
NumObservations: 314
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
LayerSizes: [13 58 65]
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Find the mean squared error of the resulting model on the test data set.
testMSE = loss(Mdl,carsTest,"MPG")testMSE = 7.3273
Create a neural network with low error by using the OptimizeHyperparameters argument. This argument causes fitrnet to search for hyperparameters that give a model with low cross-validation error. Use the hyperparameters function to specify larger-than-default values for the number of layers used and the layer size range.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Displacement,Horsepower, ... Model_Year,Origin,Weight,MPG);
Delete rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.20); trainingIdx = training(c); % Training set indices carsTrain = cars(trainingIdx,:); testIdx = test(c); % Test set indices carsTest = cars(testIdx,:);
List the hyperparameters available for this problem of fitting the MPG response.
params = hyperparameters("fitrnet",carsTrain,"MPG"); for ii = 1:length(params) disp(ii);disp(params(ii)) end
1
optimizableVariable with properties:
Name: 'NumLayers'
Range: [1 3]
Type: 'integer'
Transform: 'none'
Optimize: 1
2
optimizableVariable with properties:
Name: 'Activations'
Range: {'relu' 'tanh' 'sigmoid' 'none'}
Type: 'categorical'
Transform: 'none'
Optimize: 1
3
optimizableVariable with properties:
Name: 'Standardize'
Range: {'true' 'false'}
Type: 'categorical'
Transform: 'none'
Optimize: 1
4
optimizableVariable with properties:
Name: 'Lambda'
Range: [3.1847e-08 318.4713]
Type: 'real'
Transform: 'log'
Optimize: 1
5
optimizableVariable with properties:
Name: 'LayerWeightsInitializer'
Range: {'glorot' 'he'}
Type: 'categorical'
Transform: 'none'
Optimize: 0
6
optimizableVariable with properties:
Name: 'LayerBiasesInitializer'
Range: {'zeros' 'ones'}
Type: 'categorical'
Transform: 'none'
Optimize: 0
7
optimizableVariable with properties:
Name: 'Layer_1_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
8
optimizableVariable with properties:
Name: 'Layer_2_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
9
optimizableVariable with properties:
Name: 'Layer_3_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
10
optimizableVariable with properties:
Name: 'Layer_4_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 0
11
optimizableVariable with properties:
Name: 'Layer_5_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 0
To try more layers than the default of 1 through 3, set the range of NumLayers (optimizable variable 1) to its maximum allowable size, [1 5]. Also, set Layer_4_Size and Layer_5_Size (optimizable variables 10 and 11, respectively) to be optimized.
params(1).Range = [1 5]; params(10).Optimize = true; params(11).Optimize = true;
Set the range of all layer sizes (optimizable variables 7 through 11) to [1 400] instead of the default [1 300].
for ii = 7:11 params(ii).Range = [1 400]; end
Train a regression neural network using the OptimizeHyperparameters argument set to params. For reproducibility, set the AcquisitionFunctionName to "expected-improvement-plus" in a HyperparameterOptimizationOptions structure. To attempt to get a better solution, set the number of optimization steps to 60 instead of the default 30.
rng("default") % For reproducibility Mdl = fitrnet(carsTrain,"MPG","OptimizeHyperparameters",params, ... "HyperparameterOptimizationOptions", ... struct("AcquisitionFunctionName","expected-improvement-plus", ... "MaxObjectiveEvaluations",60))
|============================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 1 | Best | 4.9294 | 0.35241 | 4.9294 | 4.9294 | sigmoid | false | 70.242 | [ 3 22 223] |
| 2 | Best | 2.211 | 3.976 | 2.211 | 2.3191 | relu | true | 0.089397 | [ 2 95] |
| 3 | Accept | 2.7225 | 23.043 | 2.211 | 2.2929 | sigmoid | false | 2.5899e-07 | [303 60 59] |
| 4 | Accept | 3.5246 | 4.4994 | 2.211 | 2.2883 | relu | false | 5.1748e-05 | [102 5 15 1] |
| 5 | Accept | 2.2357 | 3.2875 | 2.211 | 2.2164 | relu | true | 0.095678 | [ 2 68] |
| 6 | Accept | 3.0174 | 1.3174 | 2.211 | 2.2144 | relu | true | 0.0031767 | [ 2 1] |
| 7 | Accept | 2.3385 | 0.64635 | 2.211 | 2.2199 | relu | true | 0.043248 | 2 |
| 8 | Accept | 4.8512 | 0.52613 | 2.211 | 2.2199 | relu | true | 3.387 | [ 2 23 5 1] |
| 9 | Accept | 2.4583 | 0.16388 | 2.211 | 2.2236 | relu | true | 1.0849 | [ 1 10] |
| 10 | Accept | 3.1863 | 3.8647 | 2.211 | 2.2237 | relu | true | 0.061861 | [ 63 1 1 112] |
| 11 | Accept | 3.8592 | 3.3615 | 2.211 | 2.2235 | relu | true | 0.20233 | [ 2 45 1 4 59] |
| 12 | Accept | 3.3752 | 3.4719 | 2.211 | 2.2111 | relu | true | 1.556e-05 | [ 4 18 1 104] |
| 13 | Accept | 6.4116 | 0.15784 | 2.211 | 2.2198 | relu | true | 287.34 | [ 34 196] |
| 14 | Accept | 2.3537 | 0.21589 | 2.211 | 2.2104 | relu | true | 5.3986 | [ 2 12] |
| 15 | Accept | 3.1122 | 0.077105 | 2.211 | 2.2109 | relu | true | 7.2543 | 1 |
| 16 | Accept | 6.4092 | 0.11676 | 2.211 | 2.2142 | relu | true | 241.19 | [ 1 389] |
| 17 | Best | 2.1517 | 0.69926 | 2.1517 | 2.1523 | relu | true | 0.24096 | 4 |
| 18 | Best | 2.1273 | 0.87139 | 2.1273 | 2.1274 | relu | true | 0.11077 | 5 |
| 19 | Accept | 4.1318 | 0.14418 | 2.1273 | 2.1274 | sigmoid | false | 4.8026e-06 | [ 12 106 59] |
| 20 | Accept | 2.2859 | 0.61843 | 2.1273 | 2.1269 | relu | true | 8.3707 | [ 2 9 1 5 9] |
|============================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 21 | Accept | 2.1981 | 11.621 | 2.1273 | 2.1265 | relu | true | 4.0719 | [203 124 1 62] |
| 22 | Accept | 4.1318 | 0.117 | 2.1273 | 2.1269 | sigmoid | false | 5.7744e-08 | [317 4 60 1] |
| 23 | Accept | 2.9406 | 2.6457 | 2.1273 | 2.1268 | relu | true | 7.2868 | [ 23 7 1 373] |
| 24 | Accept | 5.4267 | 0.15109 | 2.1273 | 2.1276 | relu | true | 3.4444 | [ 1 253 1] |
| 25 | Accept | 3.5359 | 1.7515 | 2.1273 | 2.1276 | relu | true | 36.471 | [ 51 3 204 71] |
| 26 | Accept | 4.1542 | 1.3619 | 2.1273 | 2.1276 | relu | true | 1.2334 | [ 5 4 1 95] |
| 27 | Accept | 2.3033 | 15.761 | 2.1273 | 2.1276 | relu | true | 0.028889 | [ 42 348] |
| 28 | Accept | 4.1318 | 0.093199 | 2.1273 | 2.1276 | sigmoid | false | 5.9314e-08 | [109 9] |
| 29 | Accept | 3.0644 | 18.95 | 2.1273 | 2.1276 | sigmoid | false | 3.2982e-08 | [388 3 331] |
| 30 | Accept | 2.8076 | 4.1115 | 2.1273 | 2.1277 | relu | true | 0.00077627 | 183 |
| 31 | Accept | 3.3041 | 3.4421 | 2.1273 | 2.1277 | relu | true | 2.1595e-05 | 116 |
| 32 | Accept | 3.1379 | 11.325 | 2.1273 | 2.1276 | relu | true | 2.2732e-05 | [187 41] |
| 33 | Accept | 3.3071 | 6.2584 | 2.1273 | 2.1277 | relu | true | 2.7221e-07 | [120 23] |
| 34 | Accept | 2.2511 | 4.5188 | 2.1273 | 2.1277 | relu | true | 2.6888 | [ 2 104 142 60] |
| 35 | Accept | 2.3491 | 7.7419 | 2.1273 | 2.1277 | relu | true | 4.3755 | [ 1 322 277 53] |
| 36 | Accept | 6.3658 | 0.2106 | 2.1273 | 2.129 | relu | true | 60.596 | [ 4 17 12 47] |
| 37 | Accept | 2.1727 | 4.9758 | 2.1273 | 2.1291 | relu | true | 0.0059602 | [ 2 110] |
| 38 | Accept | 2.5005 | 28.335 | 2.1273 | 2.1288 | relu | true | 0.052893 | [252 99 208 55] |
| 39 | Accept | 2.2474 | 31.45 | 2.1273 | 2.1301 | relu | true | 6.086 | [356 136 307 70] |
| 40 | Best | 2.0745 | 37.552 | 2.0745 | 2.0746 | relu | true | 0.55888 | [288 115 213 120] |
|============================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 41 | Accept | 2.0896 | 26.315 | 2.0745 | 2.0747 | relu | true | 0.98992 | [270 74 258 28] |
| 42 | Accept | 4.1421 | 0.53203 | 2.0745 | 2.0746 | relu | true | 13.353 | [ 4 376 1 149] |
| 43 | Accept | 2.6447 | 5.5647 | 2.0745 | 2.0746 | relu | true | 0.026383 | [ 18 118 1 23] |
| 44 | Accept | 2.4817 | 27.009 | 2.0745 | 2.0747 | relu | true | 0.013213 | [389 175] |
| 45 | Accept | 2.3857 | 6.6975 | 2.0745 | 2.0746 | relu | true | 0.0012278 | [ 4 386] |
| 46 | Accept | 2.0888 | 6.0115 | 2.0745 | 2.0746 | relu | true | 0.12715 | 354 |
| 47 | Accept | 4.0279 | 1.866 | 2.0745 | 2.0747 | relu | true | 3.1997 | [ 8 46 1 7] |
| 48 | Accept | 2.1107 | 3.9274 | 2.0745 | 2.0747 | relu | true | 0.87573 | [ 75 3] |
| 49 | Accept | 2.8679 | 17.581 | 2.0745 | 2.0747 | relu | true | 0.014349 | [382 19 2 217] |
| 50 | Accept | 2.12 | 31.823 | 2.0745 | 2.0748 | relu | true | 1.4981 | [ 9 250 205 316] |
| 51 | Accept | 2.0956 | 9.3003 | 2.0745 | 2.0749 | relu | true | 0.50519 | [ 13 25 234] |
| 52 | Accept | 2.0788 | 20.963 | 2.0745 | 2.0748 | relu | true | 0.20245 | [ 30 340 72] |
| 53 | Accept | 2.0793 | 15.073 | 2.0745 | 2.0749 | relu | true | 0.30508 | [230 27 157] |
| 54 | Best | 2.0571 | 14.353 | 2.0571 | 2.0572 | relu | true | 0.40191 | [ 58 58 83 4] |
| 55 | Accept | 2.2477 | 5.5372 | 2.0571 | 2.0572 | relu | true | 0.056099 | [ 8 2 166] |
| 56 | Accept | 2.2329 | 9.6228 | 2.0571 | 2.0571 | relu | true | 0.15146 | [ 1 46 169 9] |
| 57 | Accept | 2.2506 | 11.931 | 2.0571 | 2.0571 | relu | true | 0.0068432 | [ 2 263 19] |
| 58 | Accept | 2.2439 | 6.1584 | 2.0571 | 2.0572 | relu | true | 0.0037586 | [ 2 191 2] |
| 59 | Accept | 6.3612 | 0.15672 | 2.0571 | 2.0572 | relu | true | 56.064 | [ 19 2 2 1 9] |
| 60 | Accept | 2.7839 | 5.6539 | 2.0571 | 2.0573 | relu | true | 0.011315 | [ 18 33 49] |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 60 reached.
Total function evaluations: 60
Total elapsed time: 494.8036 seconds
Total objective function evaluation time: 469.8626
Best observed feasible point:
Activations Standardize Lambda LayerSizes
___________ ___________ _______ ____________________
relu true 0.40191 58 58 83 4
Observed objective function value = 2.0571
Estimated objective function value = 2.0573
Function evaluation time = 14.3527
Best estimated feasible point (according to models):
Activations Standardize Lambda LayerSizes
___________ ___________ _______ ____________________
relu true 0.40191 58 58 83 4
Estimated objective function value = 2.0573
Estimated function evaluation time = 14.3565

Mdl =
RegressionNeuralNetwork
PredictorNames: {'Acceleration' 'Displacement' 'Horsepower' 'Model_Year' 'Origin' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: 5
ResponseTransform: 'none'
NumObservations: 314
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
LayerSizes: [58 58 83 4]
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Find the mean squared error of the resulting model on the test data set.
testMSE = loss(Mdl,carsTest,"MPG")testMSE = 7.1939
Since R2024b
Create a regression neural network with more than one response variable.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Displacement, Horsepower, and so on, as well as the response variables Acceleration and MPG. Display the first eight rows of the table.
load carbig cars = table(Displacement,Horsepower,Model_Year, ... Origin,Weight,Acceleration,MPG); head(cars)
Displacement Horsepower Model_Year Origin Weight Acceleration MPG
____________ __________ __________ _______ ______ ____________ ___
307 130 70 USA 3504 12 18
350 165 70 USA 3693 11.5 15
318 150 70 USA 3436 11 18
304 150 70 USA 3433 12 16
302 140 70 USA 3449 10.5 17
429 198 70 USA 4341 10 15
454 220 70 USA 4354 9 14
440 215 70 USA 4312 8.5 14
Remove rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets. Use approximately 85% of the observations to train a neural network model, and 15% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility c = cvpartition(height(cars),"Holdout",0.15); carsTrain = cars(training(c),:); carsTest = cars(test(c),:);
Train a multiresponse neural network regression model by passing the carsTrain training data to the fitrnet function. For better results, specify to standardize the predictor data.
Mdl = fitrnet(carsTrain,["Acceleration","MPG"], ... Standardize=true)
Mdl =
RegressionNeuralNetwork
PredictorNames: {'Displacement' 'Horsepower' 'Model_Year' 'Origin' 'Weight'}
ResponseName: {'Acceleration' 'MPG'}
CategoricalPredictors: 4
ResponseTransform: 'none'
NumObservations: 334
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'none'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Mdl is a trained RegressionNeuralNetwork model. You can use dot notation to access the properties of Mdl. For example, you can specify Mdl.ConvergenceInfo to get more information about the model convergence.
Evaluate the performance of the regression model on the test set by computing the test mean squared error (MSE). Smaller MSE values indicate better performance. Return the loss for each response variable separately by setting the OutputType name-value argument to "per-response".
testMSE = loss(Mdl,carsTest,["Acceleration","MPG"], ... OutputType="per-response")
testMSE = 1×2
1.5341 4.8245
Predict the response values for the observations in the test set. Return the predicted response values as a table.
predictedY = predict(Mdl,carsTest,OutputType="table")predictedY=58×2 table
Acceleration MPG
____________ ______
9.3612 13.567
15.655 21.406
17.921 17.851
11.139 13.433
12.696 10.32
16.498 17.977
16.227 22.016
12.165 12.926
12.691 12.072
12.424 14.481
16.974 22.152
15.504 24.955
11.068 13.874
11.978 12.664
14.926 10.134
15.638 24.839
⋮
Input Arguments
Sample data used to train the model, specified as a table. Each row of
Tbl corresponds to one observation, and each column corresponds
to one predictor variable. Multicolumn variables and cell arrays other than cell arrays
of character vectors are not allowed.
Optionally,
Tblcan contain columns for the response variables and a column for the observation weights. Each response variable and the weight values must be numeric vectors.You must specify the response variables in
Tblby usingResponseVarNameorformulaand specify the observation weights inTblby usingWeights.When you specify the response variables by using
ResponseVarName,fitrnetuses the remaining variables as predictors. To use a subset of the remaining variables inTblas predictors, specify predictor variables by usingPredictorNames.When you define a model specification by using
formula,fitrnetuses a subset of the variables inTblas predictor variables and response variables, as specified informula.
If
Tbldoes not contain the response variables, then specify them by usingY. IfYis a vector, then the length of the response variable and the number of rows inTblmust be equal. IfYis a matrix, thenYandTblmust have the same number of rows. To use a subset of the variables inTblas predictors, specify predictor variables by usingPredictorNames.
Data Types: table
Response variable names, specified as the names of variables in
Tbl. Each response variable must be a numeric vector.
You must specify ResponseVarName as a character vector, string
array, or cell array of character vectors. For example, if Tbl stores
the response variable Y as Tbl.Y, then specify it
as "Y". Otherwise, the software treats the Y
column of Tbl as a predictor when training the model.
Data Types: char | string | cell
Explanatory model of the response variables and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y1,Y2~x1+x2+x3". In this form, Y1 and
Y2 represent the response variables, and x1,
x2, and x3 represent the predictor
variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula, except for observation weights (if specified).
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Response data, specified as a numeric vector, matrix, or table.
To use one response variable, specify
Yas a vector. The length ofYmust be equal to the number of observations inXorTbl.To use multiple response variables, specify
Yas a matrix or table, where each column corresponds to a response variable.Yand the predictor data (XorTbl) must have the same number of rows.
Data Types: single | double | table
Predictor data used to train the model, specified as a numeric matrix.
By default, the software treats each row of X as one
observation, and each column as one predictor.
X and Y must have the same number of
observations.
To specify the names of the predictors in the order of their appearance in
X, use the PredictorNames name-value
argument.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time.
Data Types: single | double
Note
When training a model with one response variable, the software treats
NaN, empty character vector (''), empty string
(""), <missing>, and
<undefined> elements as missing values, and removes observations
with any of these characteristics:
Missing value in the response (for example,
YorValidationData{2})At least one missing value in a predictor observation (for example, row in
XorValidationData{1})NaNvalue or0weight (for example, value inWeightsorValidationData{3})
When you train a model with multiple response variables, remove missing values from the
data arguments before passing them to fitrnet.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: fitrnet(X,Y,LayerSizes=[10 10],Activations=["relu","tanh"])
specifies to create a neural network with two fully connected layers, each with 10 outputs.
The first layer uses a rectified linear unit (ReLU) activation function, and the second uses
a hyperbolic tangent activation function.
Neural Network Options
Sizes of the fully connected layers in the neural network model, specified as one of these values:
Vector of positive integers — The ith element of
LayerSizesis the number of outputs in the ith fully connected layer of the neural network model.LayerSizesdoes not include the size of the final fully connected layer. For more information, see Neural Network Structure.[](since R2025a) — Use the neural network architecture specified by theNetworkargument.
When Network is [], the default value is
10. Otherwise, the default value is []. If you
specify the neural network architecture using the Network
argument, then you must not change the value of the LayerSizes
argument.
Example: LayerSizes=[100 25 10]
Activation functions for the fully connected layers of the neural network model, specified as one of these values:
String scalar or character vector — Use the specified activation function for each of the fully connected layers of the model.
String array or cell array of character vectors — Use the ith element of
Activationsfor the ith fully connected layer of the model.""(since R2025a) — Use the neural network architecture specified by theNetworkargument.
Specify the activation functions using one or more of these values:
| Value | Description |
|---|---|
"relu" | Rectified linear unit (ReLU) function — Performs a threshold operation on each element of the input, where any value less than zero is set to zero, that is, |
"tanh" | Hyperbolic tangent (tanh) function — Applies the |
"sigmoid" | Sigmoid function — Performs the following operation on each input element: |
"none" | Identity function — Returns each input element without performing any transformation, that is, f(x) = x |
When Network is [], the default value is
"relu". Otherwise, the default value is []. If
you specify the neural network architecture using the Network
argument, then you must not change the value of the Activations
argument.
Example: Activations="sigmoid"
Example: Activations=["relu","tanh"]
Function to initialize the fully connected layer weights, specified as one of these values:
"glorot"— Initialize the weights with the Glorot initializer [1] (also known as the Xavier initializer). For each layer, the Glorot initializer independently samples from a uniform distribution with zero mean and variance2/(I+O), whereIis the input size andOis the output size for the layer."he"— Initialize the weights with the He initializer [2]. For each layer, the He initializer samples from a normal distribution with zero mean and variance2/I, whereIis the input size for the layer.""(since R2025a) — Initialize the weights using the initializers specified by the layers in theNetworkargument.
When Network is [], the default value is
"glorot". Otherwise, the default value is "".
If you specify the neural network architecture using the Network
argument, then you must not change the value of the
LayerWeightsInitializer argument.
Example:
LayerWeightsInitializer="he"
Data Types: char | string
Type of initial fully connected layer biases, specified as one of these values:
"zeros"— Initialize the biases with a vector of zeros."ones"— Initialize the biases with a vector of ones.""(since R2025a) — Initialize the biases using the initializers specified by the layers in theNetworkargument.
When Network is [], the default value is
"zeros". Otherwise, the default value is "".
If you specify the neural network architecture using the Network
argument, then you must not change the value of the
LayerBiasesInitializer argument.
Example:
LayerBiasesInitializer="ones"
Data Types: char | string
Since R2025a
Custom neural network architecture, specified as one of these values:
[]— Use the neural network architecture and layer configuration defined by theLayerSizes,Activations,LayerWeightsInitializer, andLayerBiasesInitializerarguments.Layer array (requires Deep Learning Toolbox™) — Use the neural network architecture specified by the layer array. For a list of available layers, see List of Deep Learning Layers (Deep Learning Toolbox).
dlnetworkobject (requires Deep Learning Toolbox) — Use the neural network architecture specified by thedlnetwork(Deep Learning Toolbox) object.
For layer array and dlnetwork input, the network must have a single
feature input layer as input with an input size that matches the number of predictors of
the input data. The output size of the network must match the number of responses. Do
not change the LayerSizes, Activations,
LayerWeightsInitializer, and
LayerBiasesInitializer arguments.
This argument does not support input data with categorical predictors.
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns
and specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a table or for
multiresponse regression.
Example: ObservationsIn="columns"
Data Types: char | string
Regularization term strength, specified as a nonnegative scalar. The software composes the objective function for minimization from the mean squared error (MSE) loss function and the ridge (L2) penalty term.
Example: Lambda=1e-4
Data Types: single | double
Flag to standardize the predictor data, specified as a numeric or logical
0 (false) or 1
(true). If you set Standardize to
true, then the software centers and scales each numeric predictor
variable by the corresponding column mean and standard deviation. The software does
not standardize categorical predictors.
If you specify the neural network architecture using the
Network argument, then to standardize the predictors using the
Standardize argument, the input layer of the network must not
perform normalization.
Example: Standardize=true
Data Types: single | double | logical
Since R2024b
Flag to standardize the response data before fitting the model, specified as a
numeric or logical 0 (false) or
1 (true). If you set
StandardizeResponses to true, then the
software centers and scales each response variable by the corresponding column mean
and standard deviation.
Example: StandardizeResponses=true
Data Types: single | double | logical
Convergence Control Options
Verbosity level, specified as 0 or 1. The
Verbose name-value argument controls the amount of diagnostic
information that fitrnet displays at the command
line.
| Value | Description |
|---|---|
0 | fitrnet does not display diagnostic
information. |
1 | fitrnet periodically displays diagnostic
information. |
By default, StoreHistory is set to
true and fitrnet stores the diagnostic
information inside of Mdl. Use
Mdl.TrainingHistory to access the diagnostic information.
Example: Verbose=1
Data Types: single | double
Frequency of verbose printing, which is the number of iterations between printing diagnostic information at the command line, specified as a positive integer scalar. A value of 1 indicates to print diagnostic information at every iteration.
Note
To use this name-value argument, you must set
Verbose to
1.
Example: VerboseFrequency=5
Data Types: single | double
Flag to store the training history, specified as a numeric or logical
0 (false) or 1
(true). If StoreHistory is set to
true, then the software stores diagnostic information inside of
Mdl, which you can access by using
Mdl.TrainingHistory.
Example: StoreHistory=false
Data Types: single | double | logical
Initial step size, specified as a positive scalar or "auto". By default,
fitrnet does not use the initial step size to determine the
initial Hessian approximation used in training the model (see Training Solver). However, if you
specify an initial step size , then the initial inverse-Hessian approximation is . is the initial gradient vector, and is the identity matrix.
To have fitrnet determine an initial step size automatically, specify the
value as "auto". In this case, the function determines the initial
step size by using . is the initial step vector, and is the vector of unconstrained initial weights and biases.
Example: InitialStepSize="auto"
Data Types: single | double | char | string
Maximum number of training iterations, specified as a positive integer scalar.
The software returns a trained model regardless of whether the training routine
successfully converges. Mdl.ConvergenceInfo contains convergence
information.
Example: IterationLimit=1e8
Data Types: single | double
Relative gradient tolerance, specified as a nonnegative scalar.
Let be the loss function at training iteration t, be the gradient of the loss function with respect to the weights and biases at iteration t, and be the gradient of the loss function at an initial point. If , where , then the training process terminates.
Example: GradientTolerance=1e-5
Data Types: single | double
Loss tolerance, specified as a nonnegative scalar.
If the function loss at some iteration is smaller than LossTolerance, then the training process terminates.
Example: LossTolerance=1e-8
Data Types: single | double
Step size tolerance, specified as a nonnegative scalar.
If the step size at some iteration is smaller than StepTolerance, then the training process terminates.
Example: StepTolerance=1e-4
Data Types: single | double
Validation data for training convergence detection, specified as a cell array or a table.
During the training process, the software periodically estimates the validation loss by using ValidationData. If the validation loss increases more than ValidationPatience times consecutively, then the software terminates the training.
You can specify ValidationData as a table if you use a table Tbl of predictor data that contains the response variable. In this case, ValidationData must contain the same predictors and response contained in Tbl. The software does not apply weights to observations, even if Tbl contains a vector of weights. To specify weights, you must specify ValidationData as a cell array.
If you specify ValidationData as a cell array, then it must have the following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of responses, then it must have the same number of elements as the number of observations inValidationData{1}. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, you can specify
ValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify the neural network architecture using the
Network argument, then ValidationData must
not contain observation weights.
If you specify ValidationData and want to display the
validation loss at the command line, set Verbose to
1.
Data Types: table | cell
Number of iterations between validation evaluations, specified as a positive integer scalar. A value of 1 indicates to evaluate validation metrics at every iteration.
Note
To use this name-value argument, you must specify ValidationData.
Example: ValidationFrequency=5
Data Types: single | double
Stopping condition for validation evaluations, specified as a nonnegative integer
scalar. Training stops if the validation loss is greater than or equal to the minimum
validation loss computed so far, ValidationPatience times in a row.
You can check the Mdl.TrainingHistory table to see the running
total of times that the validation loss is greater than or equal to the minimum
(Validation Checks).
Example: ValidationPatience=10
Data Types: single | double
Note
Validation data options (ValidationData,
ValidationFrequency, and ValidationPatience)
are not supported for multiresponse regression.
Other Regression Options
Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the
predictor data is in a table (Tbl), fitrnet
assumes that a variable is categorical if it is a logical vector, categorical vector, character
array, string array, or cell array of character vectors. If the predictor data is a matrix
(X), fitrnet assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
For the identified categorical predictors, fitrnet creates
dummy variables using two different schemes, depending on whether a categorical variable
is unordered or ordered. For an unordered categorical variable,
fitrnet creates one dummy variable for each level of the
categorical variable. For an ordered categorical variable,
fitrnet creates one less dummy variable than the number of
categories. For details, see Automatic Creation of Dummy Variables.
Example: CategoricalPredictors="all"
Data Types: single | double | logical | char | string | cell
Predictor variable names, specified as a string array of unique names or cell
array of unique character vectors. The functionality of
PredictorNames depends on the way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the predictor order inX. Assuming thatXhas the default orientation, with observations in rows and predictors in columns,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrnetuses only the variables inPredictorNamesas predictors during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of any response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Response variable names, specified as a character vector, string array, or cell array of character vectors.
If you supply
Y, then you can useResponseNameto specify names for the response variables.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="Response"
Example: ResponseName=["Response1","Response2"]
Data Types: char | string | cell
Function for transforming raw response values, specified as a function handle or
function name. The default is "none", which means
@(y)y, or no transformation. The function must accept the
original response values and return an output of the same size (the transformed
response values).
Example: Suppose you create a function handle that applies an exponential
transformation to an input vector by using myfunction = @(y)exp(y).
Then, you can specify the response transformation as
ResponseTransform=myfunction.
Data Types: char | string | function_handle
Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.
If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as "W". Otherwise, the software treats all columns of Tbl, including W, as predictors when training the model.
By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.
fitrnet normalizes the weights to sum to 1.
Inf weights are not supported. If you specify the neural network architecture using the Network
argument, then Weights must be a vector of ones.
Data Types: single | double | char | string
Cross-Validation Options
Flag to train a cross-validated model, specified as "on" or
"off".
If you specify "on", then the software trains a cross-validated
model with 10 folds.
You can override this cross-validation setting using the
CVPartition, Holdout,
KFold, or Leaveout name-value argument.
You can use only one cross-validation name-value argument at a time to create a
cross-validated model.
Alternatively, cross-validate later by passing Mdl to
crossval.
Example: Crossval="on"
Data Types: char | string
Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the
indexing for the training and validation sets.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Suppose you create a random partition for 5-fold cross-validation on 500
observations by using cvp = cvpartition(500,KFold=5). Then, you can
specify the cross-validation partition by setting
CVPartition=cvp.
Fraction of the data used for holdout validation, specified as a scalar value in the range
(0,1). If you specify Holdout=p, then the software completes these
steps:
Randomly select and reserve
p*100% of the data as validation data, and train the model using the rest of the data.Store the compact trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Holdout=0.1
Data Types: double | single
Number of folds to use in the cross-validated model, specified as a positive integer value
greater than 1. If you specify KFold=k, then the software completes
these steps:
Randomly partition the data into
ksets.For each set, reserve the set as validation data, and train the model using the other
k– 1 sets.Store the
kcompact trained models in ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: KFold=5
Data Types: single | double
Leave-one-out cross-validation flag, specified as "on" or
"off". If you specify Leaveout="on", then for
each of the n observations (where n is the number
of observations, excluding missing observations, specified in the
NumObservations property of the model), the software completes
these steps:
Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Leaveout="on"
Data Types: char | string
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparametersname-value argument. You can modify the cross-validation forOptimizeHyperparametersonly by using theHyperparameterOptimizationOptionsname-value argument.Cross-validation options are not supported for multiresponse regression.
Hyperparameter Optimization Options
Parameters to optimize, specified as one of the following:
"none"— Do not optimize."auto"— Use["Activations","Lambda","LayerSizes","Standardize"]."all"— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
The optimization attempts to minimize the cross-validation loss
(error) for fitrnet by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitrnet to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
To optimize the model hyperparameters, the Network
argument must be []. The eligible parameters for
fitrnet are:
Activations—fitrnetoptimizesActivationsover the set["relu","tanh","sigmoid","none"].Lambda—fitrnetoptimizesLambdaover continuous values in the range[1e-5,1e5]/NumObservations, where the value is chosen uniformly in the log transformed range.LayerBiasesInitializer—fitrnetoptimizesLayerBiasesInitializerover the two values["zeros","ones"].LayerWeightsInitializer—fitrnetoptimizesLayerWeightsInitializerover the two values["glorot","he"].LayerSizes—fitrnetoptimizes over the three values1,2, and3fully connected layers, excluding the final fully connected layer.fitrnetoptimizes each fully connected layer separately over1through300sizes in the layer, sampled on a logarithmic scale.Note
When you use the
LayerSizesargument, the iterative display shows the size of each relevant layer. For example, if the current number of fully connected layers is3, and the three layers are of sizes10,79, and44respectively, the iterative display showsLayerSizesfor that iteration as[10 79 44].Note
To access up to five fully connected layers or a different range of sizes in a layer, use
hyperparametersto select the optimizable parameters and ranges.Standardize—fitrnetoptimizesStandardizeover the two values[true,false].
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault values. As an
example, this code sets the range of NumLayers to [1
5] and optimizes Layer_4_Size and
Layer_5_Size:
load carsmall params = hyperparameters("fitrnet",[Horsepower,Weight],MPG); params(1).Range = [1 5]; params(10).Optimize = true; params(11).Optimize = true;
Pass params as the value of
OptimizeHyperparameters. For an example, see Custom Hyperparameter Optimization in Neural Network.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is log(1 + cross-validation loss). To control the iterative display, set the Verbose option
of the HyperparameterOptimizationOptions name-value argument. To control
the plots, set the ShowPlots option of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Minimize Cross-Validation Error in Neural Network.
Example: OptimizeHyperparameters="auto"
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you must
also specify OptimizeHyperparameters. All the options are optional.
However, you must set ConstraintBounds and
ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Note
Hyperparameter optimization options are not supported for multiresponse regression.
Output Arguments
Trained neural network regression model, returned as a RegressionNeuralNetwork or RegressionPartitionedNeuralNetwork model object.
If you set any of the name-value arguments CrossVal,
CVPartition, Holdout,
KFold, or Leaveout, then
Mdl is a RegressionPartitionedNeuralNetwork
model object. Otherwise, Mdl is a
RegressionNeuralNetwork model object.
To reference properties of Mdl, use dot notation.
If you specify OptimizeHyperparameters and
set the ConstraintType and ConstraintBounds options of
HyperparameterOptimizationOptions, then Mdl is an
N-by-1 cell array of model objects, where N is equal
to the number of rows in ConstraintBounds. If none of the optimization
problems yields a feasible model, then each cell array value is [].
If you fit the model with the Network argument set to a layer array or dlnetwork object, then to examine the neural network architecture of the model, convert the model to a dlnetwork object using the dlnetwork (Deep Learning Toolbox) function.
Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. For an example that
shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
More About
The default neural network regression model has the following layer structure.
| Structure | Description |
|---|---|
|
| Input — This layer corresponds to the predictor data in
Tbl or X. |
First fully connected layer — This layer has 10 outputs by default.
| |
ReLU activation function —
| |
Final fully connected layer — This layer has one output for each response variable.
| |
| Output — This layer corresponds to the predicted response values. |
For an example that shows how a regression neural network model with this layer structure returns predictions, see Predict Using Layer Structure of Regression Neural Network Model.
To specify a custom neural network architecture, use the
Network
argument. (since R2025a)
Tips
Always try to standardize the numeric predictors (see
Standardize). Standardization makes predictors insensitive to the scales on which they are measured.After training a model, you can generate C/C++ code that predicts responses for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
fitrnet uses a limited-memory Broyden-Fletcher-Goldfarb-Shanno
quasi-Newton algorithm (LBFGS) [3] as its loss function
minimization technique, where the software minimizes the mean squared error (MSE). The LBFGS
solver uses a standard line-search method with an approximation to the Hessian.
References
[1] Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pp. 249–256. 2010.
[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification.” In Proceedings of the IEEE international conference on computer vision, pp. 1026–1034. 2015.
[3] Nocedal, J. and S. J. Wright. Numerical Optimization, 2nd ed., New York: Springer, 2006.
Extended Capabilities
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitrnet function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
fitrnetfits the model on a GPU if at least one of the following applies:The input argument
Xis agpuArrayobject.The input argument
Yis agpuArrayobject.The input argument
TblcontainsgpuArraypredictor or response variables.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2021afitrnet defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
You can create a neural network regression model with multiple response variables by
using the fitrnet function. Regardless of the number of response
variables, the function returns a RegressionNeuralNetwork object. You can
use the loss object function to compute the regression loss, and the
predict object function to predict the responses for new data.
In the call to fitrnet, you can specify to standardize the response
variables by using the StandardizeResponses name-value argument. You cannot use observations in rows,
validation data options, cross-validation options, or hyperparameter optimization options
when fitting a neural network model with multiple response variables.
fitrnet now supports GPU arrays.
Starting in R2023b, a cross-validated regression neural network model is a RegressionPartitionedNeuralNetwork object. In previous releases, a cross-validated regression neural network model was a RegressionPartitionedModel object.
You can create a RegressionPartitionedNeuralNetwork object in two ways:
Create a cross-validated model from a regression neural network model object
RegressionNeuralNetworkby using thecrossvalobject function.Create a cross-validated model by using the
fitrnetfunction and specifying one of the name-value argumentsCrossVal,CVPartition,Holdout,KFold, orLeaveout.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
