hinfstruct
H∞ tuning of fixed-structure controllers
Syntax
Description
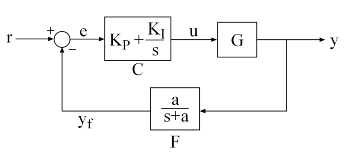
CL = hinfstruct(CL0)genss model CL0. This tuning minimizes the
H∞ norm of the closed-loop transfer
function modeled by CL0. The model CL0 represents
a closed-loop control system that includes tunable components such as controllers or
filters. CL0 can also include weighting functions that capture design
requirements.
[
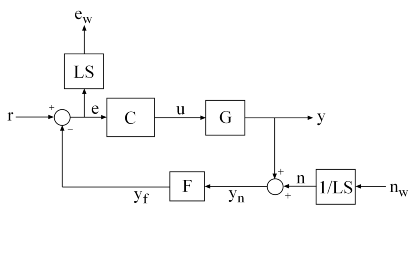
tunes the parametric controller blocks C,gamma,info]
= hinfstruct(P,C0,options)C0. This tuning minimizes the
H∞ norm of the closed-loop system
CL0 = lft(P,C0). To use this syntax, express your control
system and design requirements as a Standard Form model, as in the following
illustration.

P is a numeric LTI model that includes the fixed elements of the
control architecture. P can also include weighting functions that
capture design requirements. C0 can be a single tunable component (for
example, a Control Design Block
or a genss model) or a cell array of multiple
tunable components. C is a parametric model or cell array of parametric
models of the same type or types as C0.
Examples
Input Arguments
Output Arguments
Tips
hinfstructis related tohinfsyn, which also uses H∞ techniques to design a controller for a MIMO plant. However, unlikehinfstruct,hinfsynimposes no restriction on the structure and order of the controller. For that reason,hinfsynalways returns a smallergammathanhinfstruct. You can therefore usehinfsynto obtain a lower bound on the best achievable performance.Using
hinfstructrequires some familiarity with H∞ techniques. You must express your design requirements as frequency-weighting functions on plant inputs and outputs, as described in Formulating Design Requirements as H-Infinity Constraints. For a simpler approach to fixed-structure tuning, usesystuneorlooptune.
Algorithms
hinfstruct uses specialized nonsmooth optimization techniques to
enforce closed-loop stability and minimize the
H∞ norm as a function of the tunable
parameters. These techniques are based on the work in [1].
hinfstruct computes the
H∞ norm using the algorithm of [2] and structure-preserving eigensolvers from the SLICOT library. For more information about
the SLICOT library, see https://github.com/SLICOT.
References
[1] Apkarian, Pierre, and Dominikus Noll. "Nonsmooth H∞ Synthesis." IEEE Transactions on Automatic Control, 51, no. 1 (January 2006): 71–86. https://doi.org/10.1109/TAC.2005.860290.
[2] Bruinsma, N.A., and M. Steinbuch. "A Fast Algorithm to Compute the H∞ Norm of a Transfer Function Matrix." Systems & Control Letters, 14, no.4 (April 1990): 287–93. https://doi.org/10.1016/0167-6911(90)90049-Z.
Extended Capabilities
Version History
Introduced in R2010b