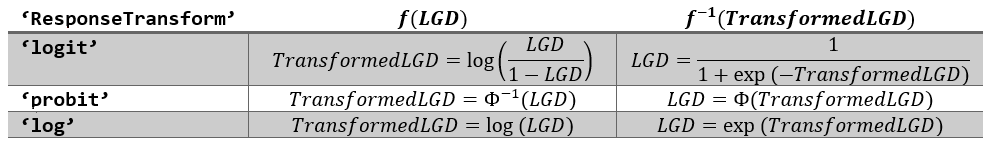Regression
Description
Create and analyze a Regression model object to calculate
the loss given default (LGD) using this workflow:
Use
fitLGDModelto create aRegressionmodel object.Use
predictto predict the LGD.Use
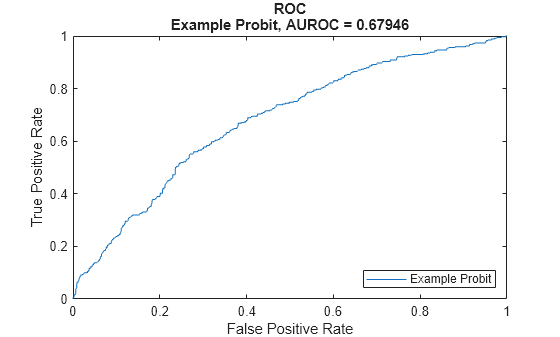
modelDiscriminationto return AUROC and ROC data. You can plot the results usingmodelDiscriminationPlot.Use
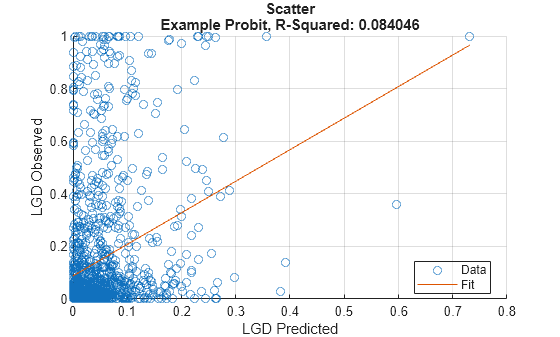
modelCalibrationto return the R-square, RMSE, correlation, and sample mean error of the predicted and observed LGD data. You can plot the results usingmodelCalibrationPlot.
Creation
Syntax
Description
RegressionLGDModel = fitLGDModel(___,Name,Value)lgdModel =
fitLGDModel(data,'regression',PredictorVars={'LTV' 'Age'
'Type'},ResponseVar="LGD",ResponseTransform="probit",BoundaryTolerance=1e-6,WeightsVar="Weights")
creates a lgdModel object using a
Regression model type.
Input Arguments
Name-Value Arguments
Properties
Object Functions
predict | Predict loss given default |
modelDiscrimination | Compute AUROC and ROC data |
modelDiscriminationPlot | Plot ROC curve |
modelCalibration | Compute R-square, RMSE, correlation, and sample mean error of predicted and observed LGDs |
modelCalibrationPlot | Scatter plot of predicted and observed LGDs |
Examples
More About
References
[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.
[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.