FIR Decimation
Perform polyphase FIR decimation
Libraries:
DSP System Toolbox /
Filtering /
Multirate Filters
DSP System Toolbox HDL Support /
Filtering
Description
The FIR Decimation block performs an efficient polyphase decimation using an integer downsampling factor M along the first dimension.
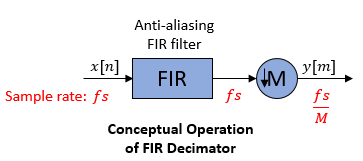
Conceptually, the FIR decimator (as shown in the schematic) consists of an
anti-aliasing FIR filter followed by a downsampler. To design an FIR anti-aliasing
filter, use the designMultirateFIR function.
The FIR filter filters the data in each channel of the input using a direct-form FIR filter. The downsampler that follows downsamples each channel of filtered data by taking every M-th sample and discarding the M – 1 samples that follow. M is the value of the decimation factor that you specify. The resulting discrete-time signal has a sample rate that is 1/M times the original sample rate.
Note that the actual block algorithm implements a direct-form FIR polyphase structure, an efficient equivalent of the combined system depicted in the diagram. For more details, see Algorithms.
Under specific conditions, this block also supports SIMD code generation. For details, see Code Generation.
Examples
FIR Decimation Using Single-Rate Processing
Use FIR Decimation block in single-rate processing mode.
FIR Decimation Using Multirate Frame-Based Processing
Use FIR Decimation block in multirate frame-based processing mode.
Polyphase Implementation of FIR Decimation Block
Polyphase implementation of the FIR decimator.
Two-Stage Multirate Narrow Lowpass Filter
Implement a two-stage multirate narrow band lowpass filter using FIR Decimation and FIR Interpolation blocks.
Ports
Input
Specify the data input as a vector or a matrix of size P-by-Q. The columns in the input signal represent Q independent channels.
The block supports variable-size input signals (frame length changes during simulation)
when you set Input processing to
Columns as channels (frame based) and
Rate options to Enforce
single-rate processing. When the block accepts
variable-size input signals, they can be of arbitrary frame length, that
is, the input frame length does not have to be a multiple of the
decimation factor. When you specify fixed-size signals, the frame length
can be arbitrary under certain conditions. For more details, see Frame-Based Processing and Sample-Based Processing.
This port is unnamed until you set Coefficient source to Input port.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Specify the numerator coefficients of the FIR filter as a vector.
The transfer function H(z) of the FIR filter is given by:
You can generate the FIR filter coefficient vector, b =
[b0,
b1, …,
bN], using one of
the DSP System Toolbox™ filter design functions such as designMultirateFIR,
firnyquist, firgr, or firceqrip.
To act as an effective anti-aliasing filter, the coefficients usually
correspond to a lowpass filter with a normalized cutoff frequency no
greater than 1/M, where M is the decimation factor.
To design such a filter, use the designMultirateFIR
function.
Coefficient values obtained through Num are tunable, that is, they can change during simulation, while their properties must remain constant.
The data type of the Num input must match the data type of the In input.
Dependencies
The Num input port appears when you set Coefficient source as Input port.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Output
Output of the FIR Decimator block, returned as a vector or a matrix.
When you set Rate options to:
Enforce single-rate processing–– The block maintains the input sample rate and decimates the signal by decreasing the output frame size by a factor of M.The output has an upper bound size of
ceil(P/M)-by-Q for an input of size P-by-Q.Allow multirate processing–– The block decimates the signal such that the output sample rate is M times slower than the input sample rate.The output frame size is the same as the input frame size.
For more details, see Frame-Based Processing and Sample-Based Processing.
This port is unnamed until you set Coefficient source to Input port.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Parameters
Coefficient source
Specify the FIR filter coefficient source as one of the following:
Dialog parameters –– Specify the filter coefficients through the FIR filter coefficients parameter in the block dialog box.
Input port –– Specify the filter coefficients through the Num input port.
Filter object –– Specify the filter using a
dsp.FIRDecimatorSystem object™.Auto –– When you select Auto, the block designs an FIR decimator using the decimation factor that you specify in Decimation factor. The
designMultirateFIRfunction designs the filter and returns the coefficients used by the block.For more information on the filter design, see Orfanidis [2].
Main Tab
Specify the lowpass FIR filter coefficients, in descending powers of
z, as a vector. By default,
designMultirateFIR(1,2) computes the filter
coefficients.
The transfer function H(z) of the FIR filter is given by:
You can generate the FIR filter coefficient vector, b =
[b0,
b1, …,
bN], using one of the
DSP System Toolbox filter design functions such as designMultirateFIR, firnyquist, firgr, or firceqrip.
To act as an effective anti-aliasing filter, the coefficients usually
correspond to a lowpass filter with a normalized cutoff frequency no greater
than 1/M, where M is the decimation factor. To
design such a filter, use the designMultirateFIR
function.
The block internally initializes all filter states to zero.
Dependencies
This parameter appears only when you set the Coefficient source to Dialog parameters.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Specify the integer factor M. The block decreases the sample rate of the input sequence by this factor.
Dependencies
This parameter appears only when you set the Coefficient source to Dialog parameters, Input port, or Auto.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Specify the FIR filter structure as either Direct
form or Direct form
transposed.
Dependencies
This parameter appears only when you set the Coefficient source to Dialog parameters, Input port, or Auto.
Specify the name of the multirate filter object that you want the block to
implement. You must specify the filter as a dsp.FIRDecimator
System object.
You can define the System object directly in the block dialog box. Alternatively, you can define the object in a MATLAB® workspace variable and specify the variable in the block dialog box.
For information on creating System objects, see Define Basic System Objects.
Dependencies
This parameter appears only when you set the Coefficient source to Filter object.
Specify how the block should process the input. You can set this parameter to one of the following options:
Columns as channels (frame based)— When you select this option, the block treats each column of the input as a separate channel.Elements as channels (sample based)— When you select this option, the block treats each element of the input as a separate channel.
Specify the method by which the block should decimate the input. You can select one of the following options:
Enforce single-rate processing— When you select this option, the block maintains the input sample rate and decimates the signal by decreasing the output frame size by a factor of M. To select this option, you must set the Input processing parameter toColumns as channels (frame based).When you set the Rate options parameter to
Enforce single-rate processing, you can use the FIR Decimation block inside triggered subsystems.Allow multirate processing— When you select this option, the block decimates the signal such that the output sample rate is M times slower than the input sample rate.
Specify whether fixed-size input signals (whose size does not change during simulation) can have an arbitrary frame length, where the frame length does not have to be a multiple of the decimation factor. The block uses this parameter setting only for fixed-size input signals and ignores this parameter if the input has a variable-size.
When the input signal is a variable-size signal, the signal can have arbitrary frame length, that is, the frame length does not have to be a multiple of the decimation factor.
For fixed-size input signals, if you:
Select the Allow arbitrary frame length for fixed-size input signals parameter, the frame length of the signal does not have to be a multiple of the decimation factor. If the input is not a multiple of the decimation factor, then the output is generally a variable-size signal. Therefore, to support arbitrary input size, the block must also support variable-size operations, which you can enable by selecting the Allow arbitrary frame length for fixed-size input signals parameter.
Clear the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length must be a multiple of the decimation factor.
Dependency
To enable this parameter, set Input processing to
Columns as channels (frame based) and
Rate options to Enforce
single-rate processing.
When you set the FIR Decimation block to the frame-based processing mode, the block can exhibit one-frame latency. In the case of one-frame latency, this parameter specifies the output of the block until the first filtered input sample is available. Specify this parameter as a scalar value to be applied to all signal channels, or as a matrix containing one value for each channel.
Cases of one-frame latency can occur when the input frame size is greater than one, and you set the Input processing and Rate options parameters of the FIR Decimation block as follows:
Input processing set to
Columns as channels (frame based)Rate options set to
Allow multirate processing
For more information on latency in the FIR Decimation block, see Latency.
Dependencies
This parameter appears only when you configure the block to perform
multirate processing by setting Rate options to
Allow multirate processing.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Click on this button to open the Filter Visualization Tool (fvtool) and display the filter response of the filter
defined in the block dialog box.
Data Types Tab
Select the rounding
mode for fixed-point operations. The default is
Floor. The filter coefficients do not obey
this parameter and always round to
Nearest.
Note
The Rounding mode and Saturate on integer overflow settings have no effect on numerical results when all the following conditions exist:
Product output is
Inherit: Inherit via internal ruleAccumulator is
Inherit: Inherit via internal ruleOutput is
Inherit: Same as accumulator
With these data type settings, the block is effectively operating in the full-precision mode.
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps the
result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Note
The Rounding mode and Saturate on integer overflow parameters have no effect on numeric results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.
With these data type settings, the block operates in full-precision mode.
Specify the coefficients data type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the coefficients data type in this block.
You can set this parameter to one of the following:
Inherit: Same word length as inputfixdt(1,16,0)orfixdt(1,16)–– Specify a data type object.
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Coefficients parameter.
to display the Data Type
Assistant, which helps you set the
Coefficients parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Dependencies
This parameter appears only when you set Coefficient
source to Dialog parameters,
Filter object, or
Auto.
When Coefficient source is set to
Filter object,
Coefficients parameter is automatically set to
Same word length as input.
Specify the minimum value of the filter coefficients. The default value is
[] (unspecified). Simulink® software uses this value to perform automatic scaling of
fixed-point data types.
Dependencies
This parameter appears only when you set Coefficient
source to Dialog parameters or
Auto.
Specify the maximum value of the filter coefficients. The default value is
[] (unspecified). Simulink software uses this value to perform automatic scaling of
fixed-point data types.
Dependencies
This parameter appears only when you set Coefficient
source to Dialog parameters or
Auto.
Specify the product output data type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the product output data type in this block.
You can set this parameter to one of the following:
Inherit: Inherit via internal ruleFor more information on this rule, see Inherit via Internal Rule.
Inherit: Same as inputfixdt(1,16,0)–– Specify a data type object.
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the Product
output parameter.
to display the Data Type
Assistant, which helps you set the Product
output parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Dependencies
When Coefficient source is set to
Filter object, Product
output parameter is automatically set to Full
precision.
Specify the accumulator data type. See Fixed-Point Data Types for illustrations depicting the use of the accumulator data type in this block.
You can set this parameter to one of the following:
Inherit: Inherit via internal rule.For more information on this rule, see Inherit via Internal Rule.
Inherit: Same as inputInherit: Same as product outputfixdt(1,16,0)–– Specify a data type object.
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Dependencies
When Coefficient source is set to
Filter object,
Accumulator parameter is automatically set to
Full precision.
Specify the output data type. See Fixed-Point Data Types for illustrations depicting the use of the output data type in this block.
You can set it to one of the following:
Inherit: Same as accumulatorInherit: Same as inputInherit: Same as product outputfixdt(1,16,0)–– Specify a data type object.
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Output parameter.
to display the Data Type
Assistant, which helps you set the
Output parameter.
See Control Data Types of Signals (Simulink) for more information.
Dependencies
When Coefficient source is set to
Filter object,
Output parameter is automatically set to
Same as accumulator.
Specify the minimum value that the block should output. The default value
is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Dependencies
This parameter appears only when you set Coefficient
source to Dialog parameters,
Input port, or
Auto.
Specify the maximum value that the block should output. The default value
is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Dependencies
This parameter appears only when you set Coefficient
source to Dialog parameters,
Input port, or
Auto.
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
A polyphase implementation of an FIR decimator splits the lowpass FIR filter impulse response into M different subfilters, where M is the downsampling or decimation factor. For more details on the polyphase implementation, see Algorithms.
Let h(n) denote the FIR filter impulse response of length N+1 and x(n) the input signal. Decimating the filter output by a factor of M is equivalent to the downsampled convolution:
The key to the efficiency of polyphase filtering is that specific input values are only multiplied by select values of the impulse response in the downsampled convolution. For example, letting M = 2, the input values x(0),x(2),x(4), ... are combined only with the filter coefficients h(0),h(2),h(4),..., and the input values x(1),x(3),x(5), ... are combined only with the filter coefficients h(1),h(3),h(5),.... By splitting the filter coefficients into two polyphase subfilters, no unnecessary computations are performed in the convolution. The outputs of the convolutions with the polyphase subfilters are interleaved and summed to yield the filter output.
The following code demonstrates how to construct the two polyphase subfilters for the default order 35 filter.
M = 2;
Num = fir1(35,0.4);
FiltLength = length(Num);
Num = flipud(Num(:));
if (rem(FiltLength, M) ~= 0)
nzeros = M - rem(FiltLength, M);
Num = [zeros(nzeros,1); Num]; % Appending zeros
end
len = length(Num);
nrows = len / M;
PolyphaseFilt = flipud(reshape(Num, M, nrows).');The columns of PolyphaseFilt are subfilters containing the two phases of the filter in Num. For a general downsampling factor of M, there are M phases and therefore M subfilters.
When you set the Input processing parameter to Columns as
channels (frame based), the block resamples each column of the
input over time. In this mode, the block can perform either single-rate or multirate
processing. You can use the Rate options parameter to specify
how the block resamples the input.
When you set the Rate options parameter to
Enforce single-rate processing, the input and output of the block have the same sample rate. To decimate the output while maintaining the input sample rate, the block resamples the data in each column of the input such that the frame length of the output has an upper bound size ofceil(P/M), where P is the input frame length and M is the decimation factor specified in the Decimation factor parameter.In this mode, if you input a fixed-size signal (frame length does not change during simulation) and select the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length can be arbitrary and does not have to be a multiple of the decimation factor. If you clear the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length must be a multiple of the decimation factor.
In this mode, if you input a variable-size signal (frame length changes during simulation), the Allow arbitrary frame length for fixed-size input signals appears on the block dialog box but does not have any impact on the input frame length. You can input a variable-size signal of any frame length even if you do not select the Allow arbitrary frame length for fixed-size input signals parameter.
This table summarizes the support for arbitrary input frame length when you set Input processing to
Columns as channels (frame based)and Rate options toEnforce single-rate processing.Input Signal Block Support for this Signal Support for Arbitrary Input Frame Length Input Size Output Size Fixed-size input signal Yes When you select Allow arbitrary frame length for fixed-size input signals P-by-Q Upper bound size of ceil(P/M)-by-QVariable-size input signal Yes Always P-by-Q Upper bound size of ceil(P/M)-by-QFor an example that shows single-rate FIR decimation, see FIR Decimation Using Single-Rate Processing.
When you set the Rate options parameter to
Allow multirate processing, the input and output of the FIR Decimation block are of the same size, but the sample rate of the output is M times slower than that of the input. In this mode, the block treats a P-by-Q matrix input as Q independent channels. The block decimates each column of the input over time by keeping the frame size constant, and making the output frame period (Tfo) M times longer than the input frame period (Tfo = M*Tfi).In this mode, the block accepts only fixed-size signals and these signals can have arbitrary frame length.
This table summarizes the support for arbitrary input frame length when you set Input processing to
Columns as channels (frame based)and Rate options toAllow multirate processing.Input Signal Block Support for this Signal Support for Arbitrary Input Frame Length Input Size Output Size Fixed-size input signal Yes Always P-by-Q P-by-Q Variable-size input signal No Not applicable Not applicable Not applicable See FIR Decimation Using Multirate Frame-Based Processing for an example that uses the FIR Decimation block in this mode.
When you set the Input processing parameter to
Elements as channels (sample based), the block treats
a P-by-Q matrix input as
P*Q independent channels, and decimates
each channel over time. The output sample period
(Tso) is M
times longer than the input sample period
(Tso =
M*Tsi), and the input and output
sizes are identical.
In this mode, the block accepts only fixed-size signals and these signals can have an arbitrary frame length.
This table summarizes the support for arbitrary input frame length when you set
Input processing to Elements as channels
(sample based). Rate options is automatically
set to Allow multirate processing.
| Input Signal | Block Support for this Signal | Support for Arbitrary Input Frame Length | Input Size | Output Size |
|---|---|---|---|---|
| Fixed-size input signal | Yes | Always | P-by-Q | P-by-Q |
| Variable-size input signal | No | Not applicable | Not applicable | Not applicable |
When you use the FIR Decimation block in the sample-based processing mode, the block always has zero-tasking latency. Zero-tasking latency means that the block propagates the first filtered input sample (received at time t= 0) as the first output sample. That first output sample is then followed by filtered input samples M+1, 2M+1, and so on.
When you use the FIR Decimation block in the frame-based processing mode with a frame size greater than one, the block may exhibit one-frame latency. Cases of one-frame latency can occur when the input frame size is greater than one and you set the Input processing and Rate options parameters of the FIR Decimation block as follows:
Input processing =
Columns as channels (frame based)Rate options =
Allow multirate processing
In cases of one-frame latency, you can define the value of the first P
output rows by setting the Output buffer initial
conditions parameter. The default value of the Output
buffer initial conditions parameter is 0.
However, you can enter a matrix containing one value for each channel of the input,
or a scalar value to be applied to all channels. The first filtered input sample
(first filtered row of the input matrix) appears in the output as sample
P+1. That sample is then followed by filtered input samples
M+1, 2M+1, and so on.
Note
For more information on latency and the Simulink tasking modes, see Excess Algorithmic Delay (Tasking Latency) and Time-Based Scheduling and Code Generation (Simulink Coder).
The following diagram shows the data types used within the FIR Decimation block for fixed-point signals.

This diagram shows that data is stored in the input buffer with the same data type and scaling as the input. The block stores filtered data and any initial conditions in the output buffer using the output data type and scaling that you set in the block dialog box.
When at least one of the inputs to the multiplier is real, the output of the multiplier is in the product output data type. When both inputs to the multiplier are complex, the result of the multiplication is in the accumulator data type. For details on the complex multiplication performed by this block, see Multiplication Data Types.
Note
When the block input is fixed point, all internal data types are signed fixed-point values.
Algorithms
The FIR decimation filter is implemented efficiently using a polyphase structure. For more details on polyphase filters, see Polyphase Subfilters.
To derive the polyphase structure, start with the transfer function of the FIR filter:
N+1 is the length of the FIR filter.
You can rearrange this equation as follows:
M is the number of polyphase components, and its value equals the decimation factor that you specify.
You can write this equation as:
E0(zM), E1(zM), ..., EM-1(zM) are the polyphase components of the FIR filter H(z).
Conceptually, the FIR decimation filter contains a lowpass FIR filter followed by a downsampler.

Replace H(z) with its polyphase representation.

Here is the multirate noble identity for decimation.

Applying the noble identity for decimation moves the downsampling operation to before the filtering operation. This move enables you to filter the signal at a lower rate.

You can replace the delays and the decimation factor at the input with a commutator switch. The switch starts on the first branch 0 and moves in the counterclockwise direction as shown in this diagram. The accumulator at the output receives the processed input samples from each branch of the polyphase structure and accumulates these processed samples until the switch goes to branch 0. When the switch goes to branch 0, the accumulator outputs the accumulated value.

When the first input sample is delivered, the switch feeds this input to the branch 0 and the decimator computes the first output value. As more input samples come in, the switch moves in the counter clockwise direction through branches M−1, M−2, and all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the decimator outputs the next set of output values. This process continues as data keeps coming in. Every time the switch comes to the branch 0, the decimator outputs y[m]. The decimator effectively outputs one sample for every M samples it receives. Hence the sample rate at the output of the FIR decimation filter is fs/M.
References
[1] Fliege, N. J. Multirate Digital Signal Processing: Multirate Systems, Filter Banks, Wavelets. West Sussex, England: John Wiley & Sons, 1994.
[2] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.
Extended Capabilities
Generated code relies on the memcpy or
memset function (string.h) under certain
conditions.
Generate SIMD code using Intel® AVX2 code replacement library
Note
Requires Embedded Coder® license
The FIR Decimation block supports SIMD code generation using Intel AVX2 code replacement library under these conditions:
Filter structure is set to
Direct form.Input processing is set to
Columns as channels (frame based).Rate options is set to
Enforce single-rate processing.Clear the Allow arbitrary frame length for fixed-size input signals parameter.
Input signal is real-valued with real filter coefficients.
Input signal is complex-valued with real or complex filter coefficients.
Input signal has a data type of
singleordouble.
To generate SIMD code from this block using this workflow, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from Simulink Blocks.
Generate SIMD code by leveraging target hardware instruction set extensions (since R2023a)
Note
Requires Simulink Coder™ or Embedded Coder license
You can generate SIMD code for the FIR Decimation block on all Intel platforms, ARM® Cortex®-A processors, and Apple silicon processors by using the model configuration parameter Leverage target hardware instruction set extensions under these conditions:
You set Filter structure to
Direct formfor the FIR Decimation blockYou set Input processing to
Columns as channels (frame based)Input signal is real-valued with real filter coefficients
Input signal is complex-valued with real or complex filter coefficients.
Data type of the input signal is
single(ARM Cortex-A processors)Data type of the input signal is
singleordouble(Intel platforms)
In addition, configure your model appropriately. In the Modeling tab of the Simulink model window, click Model Settings and configure these parameters under Code Generation.
In the Optimization pane:
Provide a specific instruction set in the Leverage target hardware instruction set extensions parameter.
Select the Optimize reductions parameter.
Under Optimization levels, set Level to
Maximumand Priority toMaximize execution speed.
In the Interface pane, under Software environment, clear non-finite numbers.
To generate SIMD code from this block using this workflow, see Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Intel Platforms, Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Apple silicon, and Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for ARM Cortex-A Processors.
For computationally intensive operations on supported blocks, SIMD intrinsics can significantly improve the performance of the generated code on Intel platforms. For more details, see Optimize Code for Reduction Operations by Using SIMD (Simulink Coder).
For more information on SIMD code generation in DSP System Toolbox, see SIMD Code Generation.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
Note
For a FIR decimation filter with hardware-friendly control signals and simulation of HDL latency in Simulink, or for complex data with complex coefficients, use the FIR Decimator (DSP HDL Toolbox) block instead of this block.
The block has HDLDataPath as a default
architecture. This architecture provides additional configuration options that
affect HDL implementation and synthesized logic.
| HDL Block Properties | Description |
|---|---|
| InputPipeline | Number of input pipeline stages to insert in the
generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default
is |
| OutputPipeline | Number of output pipeline stages to insert in the
generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default
is |
| ConstrainedOutputPipeline | Number of registers to place at the outputs by
moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The
default is |
| FlattenFilter | Remove hierarchy of Filter subsystem from generated
HDL code. The default is
|
| DSPStyle | Synthesis attributes for multiplier mapping. The
default is |
| SharingFactor | Number of functionally equivalent resources to map to a single shared resource. The default is 0. See also Resource Sharing (HDL Coder). |
| StreamingFactor | Number of parallel data paths, or vectors, that are time multiplexed to transform into serial, scalar data paths. The default is 0, which implements fully parallel data paths. See also Streaming (HDL Coder). |
| ConstMultiplierOptimization | Canonical signed digit (CSD) or factored CSD
optimization. The default is
|
| MultiplerArchitecture | Select the multipler architecture as
linear or
shiftadd. The default is
linear. For more information,
see HDL Code Generation section in Product, Matrix
Multiply (Simulink). |
| MultiplierInputPipeline | Specify the number of pipeline stages to add at filter multiplier inputs. See also MultiplierInputPipeline (HDL Coder). |
| MultiplierOutputPipeline | Specify the number of pipeline stages to add at filter multiplier outputs. See also MultiplierOutputPipeline (HDL Coder). |
| AdderChainArchitecture | Select the adder architecture to generate linear chain or
tree structure of adders to compute sum of elements. The
default is tree. For more
information, see HDL Code Generation section in Sum (Simulink). |
| AdderOutputPipeline | Number of output pipeline stages to insert in the
generated code for addition operation. The default is
|
The block supports these data types for HDL code generation:
| Input Port | Dimension | Fixed-Point | Floating-Point | Built-in Integers | Bus | Boolean | Enumerated | Complex Signal |
|---|---|---|---|---|---|---|---|---|
| In | Scalar Vector Matrix | Yes | Half Single Double | Yes | Yes | Yes | Yes | Yes |
The block participates in these HDL optimizations to optimize the speed, and area.
Area Optimization
| Optimization | Description |
|---|---|
| Resource Sharing (HDL Coder) | Resource sharing is an area optimization in which HDL Coder identifies multiple functionally equivalent resources and replaces them with a single resource. |
| Streaming (HDL Coder) | Streaming is an area optimization in which HDL Coder transforms a vector data path to a scalar data path (or to several smaller-sized vector data paths). |
Speed Optimization
| Optimization | Description |
|---|---|
| Distributed Pipelining (HDL Coder) | Distributed pipelining, or register retiming, is a speed optimization that moves existing delays in a design to reduce the critical path while preserving functional behavior. |
| Clock-Rate Pipelining (HDL Coder) | Clock-rate pipelining is an optimization framework in HDL Coder that allows other speed and area optimizations to introduce latency at the clock rate. |
| Adaptive Pipelining (HDL Coder) | Adaptive pipelining optimization creates patterns or combination of blocks with registers that can improve the achievable clock frequency and reduce the area usage on the FPGA boards by inserting pipeline registers to the blocks in your design. |
| Critical Path Estimation (HDL Coder) | To quickly identify the most likely critical path in your design, use Critical Path Estimation. Critical path estimation speeds up the iterative process of finding the critical path. To know blocks that are characterized in critical path estimation, see Characterized Blocks (HDL Coder). |
The block has these limitations:
You must set Initial conditions to zero. HDL code generation is not supported for nonzero initial states.
When you select Dialog parameters, the following fixed-point options are not supported for HDL code generation:
Slope and Bias scaling
Programmable coefficients are not supported.
Frame-based input filters are not supported for:
Resettable and enabled subsystems
Complex input signals with complex coefficients. You can use either complex input signals and real coefficients, or complex coefficients and real input signals.
Sharing and streaming optimizations
To configure the FIR Decimation block for a frame-based input, use the following block settings:
| Frame-based input | HDL Coder supports the use of vector inputs to FIR Decimation blocks, where each element of the vector represents a sample in time. You can use an input vector of up to 512 samples. The frame-based implementation supports fixed-point input and output data types, and uses full-precision internal data types. The output is a column vector of reduced size, corresponding to your decimation factor. You can use real input signals with real coefficients, complex input signals with real coefficients, or real input signals with complex coefficients.
|
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced before R2006aIn R2024b, if you have Embedded Coder, you can generate SIMD code for the FIR Decimation block for Apple silicon processors by using the model configuration parameter Leverage target hardware instruction set extensions. For more information, see Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Apple silicon.
In R2024a, if you have Embedded Coder, you can generate SIMD code for the FIR Decimation block for ARM Cortex-A processors by using the model configuration parameter Leverage target hardware instruction set extensions.
In R2023b, if you have Embedded Coder, you can generate SIMD code for the FIR Decimation block when the input signal is complex-valued by using the model configuration parameter Leverage target hardware instruction set extensions.
In R2023a, if you have Embedded Coder, you can generate SIMD code for the FIR Decimation block on all Intel platforms by using the model configuration parameter Leverage target hardware instruction set extensions. Previously, you had to use a code replacement library to generate SIMD code. For more details, see Code Generation.
Starting in R2022b, this block supports input signals with arbitrary frame lengths when the:
Input signal is a fixed-size signal (frame length does not change during simulation) and the block allows for multirate processing
Input signal is a fixed-size signal, the block enforces single-rate processing, and you select the Allow arbitrary frame length for fixed-size input signals parameter
Input signal is a variable-size signal (frame length changes during simulation)
When this block supports an arbitrary frame length input signal, the input frame length does not have to be a multiple of the decimation factor.
For more details, see Frame-Based Processing and Sample-Based Processing.
See Also
Functions
firgr|firceqrip|firnyquist
Objects
Blocks
- Variable FIR Decimation | FIR Interpolation | FIR Rate Conversion | FIR Halfband Interpolator | FIR Halfband Decimator | IIR Halfband Interpolator | IIR Halfband Decimator | CIC Compensation Interpolator | CIC Compensation Decimator | Downsample | CIC Decimation | Digital Up-Converter | Digital Down-Converter
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)