series

Series connection of two models

collapse all in page

Syntax

sys = series(sys1,sys2)
sys = series(sys1,sys2,out1,in2)
sys = series(sys1,sys2,"name")

Description

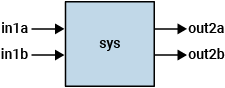
sys = series(sys1,sys2) forms the series interconnection of two dynamic system models by connecting the outputs of sys1 to the inputs of sys2, as shown in the diagram.

This command is equivalent to the direct multiplication sys = sys2*sys1. For MIMO systems, the number of inputs of sys2 must equal the number of outputs of sys1. The resulting sys has inputs u and outputs y.

example

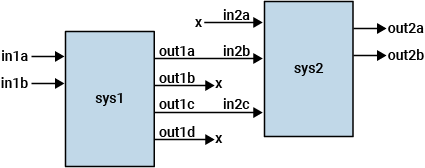
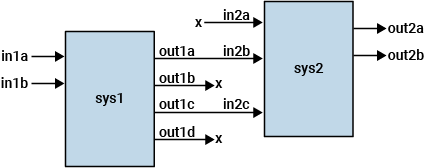
sys = series(sys1,sys2,out1,in2) forms the more general series interconnection shown in the following diagram by connecting a subset of the outputs of sys1 to a subset of the inputs of sys2.

out1 is a vector specifying the indices of the outputs of sys1 to connect. Similarly, in1 specifies the indices of the inputs of sys2 to connect to those outputs. The resulting sys has inputs u and outputs y. series drops unconnected outputs z1 of sys1 and unconnected inputs v2 of sys2.

example

sys = series(sys1,sys2,"name") connects a subset of the outputs of sys1 to a subset of the inputs of sys2 by matching signal names as defined in the OutputName and InputName properties of the models. series drops unconnected outputs of sys1 and unconnected inputs of sys2.

example

Examples

collapse all

Open Live Script

Create two SISO systems, one a state-space model and the other a transfer function.

sys1 = rss(3);
sys2 = tf(1,[1 1 1]);

Form the series connection of the two systems.

sys = series(sys1,sys2);
size(sys)
State-space model with 1 outputs, 1 inputs, and 5 states.

Connecting a transfer function with a state-space model results in another state-space model. For more information about the results of combining different model types, see Rules That Determine Model Type.

The series interconnection is equivalent to the product sys2*sys1. Check this equivalence by examining the frequency responses. 

sysm = sys2*sys1;
bodeplot(sys,'-',sysm,'--')

MATLAB figure

Open Live Script

Connect two MIMO systems in series. When number of outputs of sys1 equals the number of inputs of sys2, you can connect all sys1 outputs to all sys2 inputs. 

sys1 = rss(3,2,3);
sys2 = rss(3,3,2);
sys = series(sys1,sys2);

The resulting system has the same number of inputs as sys1 and the same number of outputs as sys2/.

size(sys)
State-space model with 3 outputs, 3 inputs, and 6 states.
Open Live Script

You can form serial connections by assigning matching names to the signals you want to connect. Starting with the four-output, two-input system sys1 and the two-output, three-input system sys2, form the series connection shown in the diagram.

Create state-space models of the two systems and name the input and output signals. 

% sys1: 4-output, 2-input
sys1 = rss(4,4,2);
sys1.InputName = ["in1a","in1b"];
sys1.OutputName = ["out1a","out1b","out1c","out1d"];
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);
sys2.InputName = ["in2a","in2b","in2c"];
sys2.OutputName = ["out2a","out2b"];

In the interconnection shown in the diagram, out1a and out1c of sys1 connect to in2b and in2c, respectively. Change the signal names so that the names of connecting signals match.

sys1.OutputName = ["ua","out1b","ub","out1d"];
sys2.InputName = ["in2a","ua","ub"];

Form the connection by calling series with the name flag.

sys = series(sys1,sys2,"name");

Examine the dimensions, inputs, and outputs of sys to confirm that the connections match the ones in the diagram. 

size(sys)
State-space model with 2 outputs, 2 inputs, and 7 states.

sys.InputName
ans = 2×1 cell
    {'in1a'}
    {'in1b'}


sys.OutputName
ans = 2×1 cell
    {'out2a'}
    {'out2b'}

As expected, the resulting sys has two outputs and two inputs, corresponding to the outputs of sys2 and the inputs of sys1, respectively.

sys drops unconnected inputs of sys2 and unconnected outputs of sys1. To form this interconnection preserving all inputs and outputs, use connect instead, specifying all the inputs and outputs you want to preserve in the resulting system.

sysc = connect(sys1,sys2,["in1a","in1b","in2a"],["out2a","out2b","out1b","out1d"]);
size(sysc)
State-space model with 4 outputs, 3 inputs, and 7 states.

sysc.InputName
ans = 3×1 cell
    {'in1a'}
    {'in1b'}
    {'in2a'}


sysc.OutputName
ans = 4×1 cell
    {'out2a'}
    {'out2b'}
    {'out1b'}
    {'out1d'}
Open Live Script

You can form series interconnections using a subset of model inputs and outputs by specifying the indices of the signals you wish to connect. Starting with the four-output, two-input system sys1 and the two-output, three-input system sys2, form the series connection shown in the diagram.

Create state-space models of the two systems. 

% sys1: 4-output, 2-input
sys1 = rss(4,4,2);
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);

To form the series connection, create vectors that specify the outputs of sys1 and the corresponding inputs of sys2 to connect. In the diagram, the first and third outputs of sys1 connect to the second and third inputs of sys2, respectively. Therefore, specify the indices as follows.

out1 = [1 3]; % out1a and out1c
in2 = [2 3];  % in2b and in2c

Form the connection and examine the size of the output.

sys = series(sys1,sys2,out1,in2);
size(sys)
State-space model with 2 outputs, 2 inputs, and 7 states.

As expected, the resulting sys has two outputs and two inputs, corresponding to the outputs of sys2 and the inputs of sys1, respectively. sys drops unconnected inputs of sys2 and unconnected outputs of sys1. To form this interconnection preserving all inputs and outputs, use connect.

Input Arguments

collapse all

Systems to connect, specified as a SISO or MIMO dynamic system model, control design block, or array of dynamic system models. Models and blocks that you can connect include:

  • Any numeric LTI model object, such as a tf, zpk, ss, frd, or pid model object.

  • A generalized or uncertain LTI model, such as a genss, genfrd, uss (Robust Control Toolbox), and ufrd (Robust Control Toolbox) model.

  • A control design block representing a tunable or uncertain block-diagram element, such as a tunablePID, tunableSS, tunableGain, tunableTF, tunableSurface, ultidyn (Robust Control Toolbox), or umargin (Robust Control Toolbox) block.

  • An AnalysisPoint block representing a location in the block diagram at which you want to extract system responses.

  • A summing junction that you create using sumblk.

  • An identified LTI model, such as an idtf (System Identification Toolbox), idss (System Identification Toolbox), or idproc (System Identification Toolbox) model.

  • A sparse model, represented by a sparss or mechss model object.

  • A time-varying or parameter-varying model, represented by an ltvss or lpvss model object.

sys1 and sys2 must be both continuous, or both discrete with the same sample time.

Outputs of sys1 to connect, specified as a vector of indices. For instance, if you want to connect the second, fourth, and fifth outputs of sys1 to three inputs of sys2, set out1 = [2,4,5].

Inputs of sys2 to connect, specified as a vector of indices. For instance, if you want to connect three outputs of sys1 to the first, third, and fourth inputs of sys2, set in2 = [1,3,4].

Output Arguments

collapse all

Interconnected system, returned as a dynamic system model whose inputs are the inputs of sys1 and whose outputs are the outputs of sys2. The type of dynamic system model depends on the types of the connected systems sys1 and sys2. For example,

  • If one of the connected systems is an ss model and the other is a numeric LTI model other than an frd model, then sys is an ss model.

  • If one of the connected systems is an frd model and the other is a numeric LTI model, then sys is an frd model. If both systems are frd models, the frequency vectors must match.

  • If one of the connected systems is an identified LTI model, then sys is also an identified model.

  • If one of the connected systems is a generalized LTI model such as a genss or uss model, then sys is also a generalized LTI model.

  • If one of the connected systems is a sparse model, then sys is also a sparse model.

If sys1 and sys2 are model arrays, then sys is a model array of the same size. Each entry in sys is the model formed by connecting the corresponding entries of the input arrays.

Version History

Introduced before R2006a

See Also

| | |