Results for
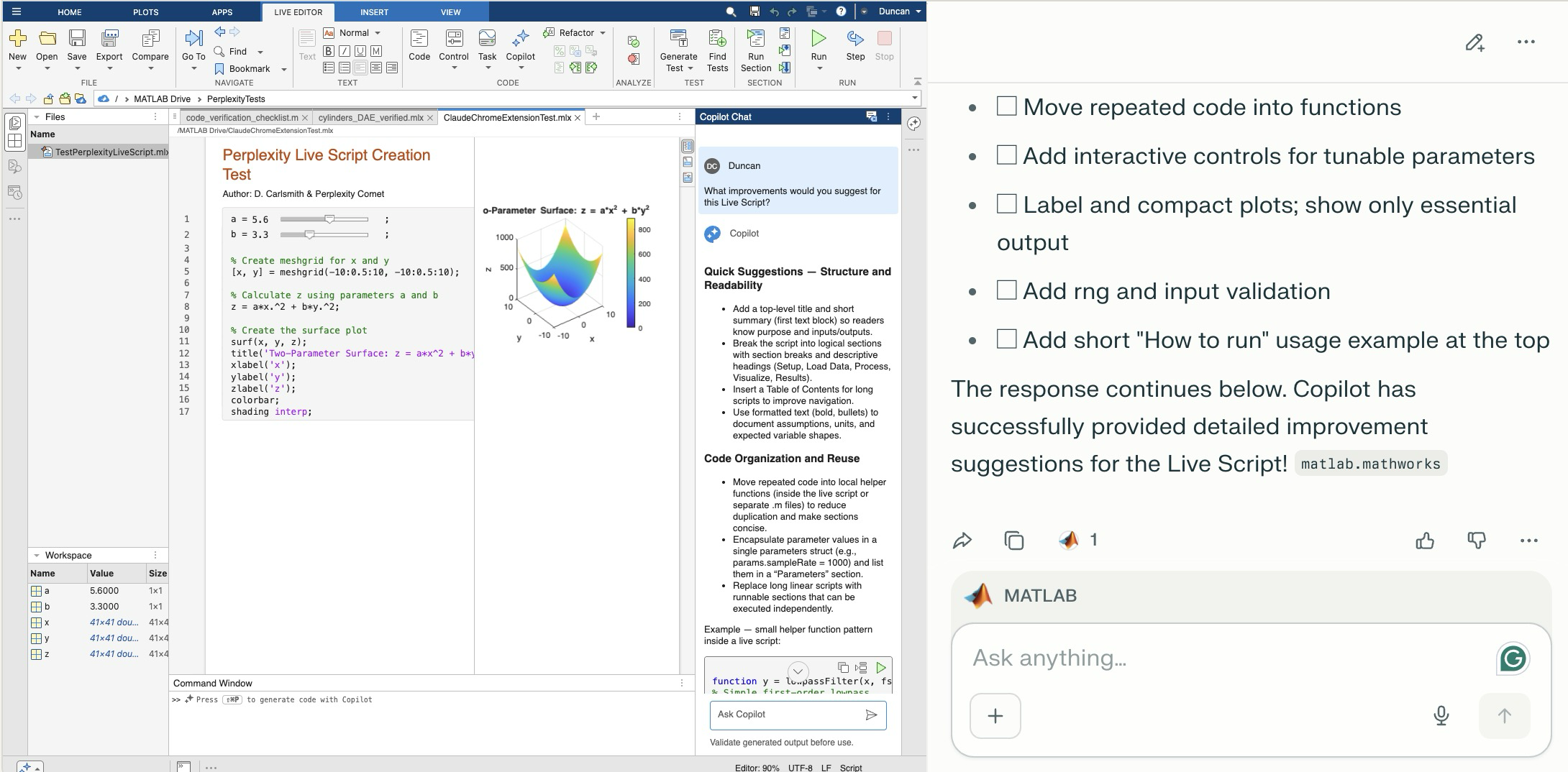
Comet browser can figure out and operate a user interface on the web including MATLAB Online. The screen shot shows MATLAB online to the left of the Comet AI. You see a test Live Script with sliders thjat Comet created in a folder (that it created). Comet is summarizing suggested improvements it requested of MATLAB Online's Copilot. Comet can plow into the arcane NASA astrophysical database interface SIMBAD, figure out how to grab information about, say, a star orbiting the black hole in the center of our galaxy and structure that information into a MATLAB data structure in a MATLAB script and run the script in MATLAB Online and display the results in the structure - it succeeded on the first try. It can do a Google Scholar citation tree search and park the results in MATLAB (success first try) or presumably in say MS Word in Office online. Presumably it can switch to a JuypterHub tab to then run a notebook or what you will. It can make mistakes, explore and discover GUI options, and recover e.g. use undo paste in MATLAB, operate in the command window, get help via the GUI if needed. Not at light speed but this seems enabling. Just released, Claude Chrome Extension Beta has similar capabilities.
Inspired in part by Christmas Trees, I'm curious about people's experience using AI to generate Matlab code.
1. Do you use AI to generate production code or just for experimentation/fun code?
2. Do you use the AI for a complete solution? Or is it more that the AI gets you most of the way there and you have to apply the finishing touches manually?
3. What level of quality would you consider the generated code? Does it follow "standard" Matlab coding practices? Is it well commented? Factored into modular functions? Argument checking? Memory efficient? Fast execution? Etc.?
4. Does the AI ever come up with a good or clever solution of which you wouldn't have thought or maybe of which you weren't even aware?
5. Is it easy/hard to express your requirements in a manner that the AI tool effectively translates into something useful?
6. Any other thoughts you'd care to share?
If you use tables extensively to perform data analysis, you may at some point have wanted to add new functionalities suited to your specific applications. One straightforward idea is to create a new class that subclasses the built-in table class. You would then benefit from all inherited existing methods.
One workaround is to create a new class that wraps a table as a Property, and re-implement all the methods that you need and are already defined for table. The is not too difficult, except for the subsref method, for which I’ll provide the code below.
Class definition
Defining a wrapper of the table class is quite straightforward. In this example, I call the class “Report” because that is what I intend to use the class for, to compute and store reports. The constructor just takes a table as input:
classdef Rapport
methods
function obj = Report(t)
if isa(t, 'Report')
obj = t;
else
obj.t_ = t;
end
end
end
properties (GetAccess = private, SetAccess = private)
t_ table = table();
end
end
I designed the constructor so that it converts a table into a Report object, but also so that if we accidentally provide it with a Report object instead of a table, it will not generate an error.
Reproducing the behaviour of the table class
Implementing the existing methods of the table class for the Report class if pretty easy in most cases.
I made use of a method called “table” in order to be able to get the data back in table format instead of a Report, instead of accessing the property t_ of the object. That method can also be useful whenever you wish to use the methods or functions already existing for tables (such as writetable, rowfun, groupsummary…).
classdef Rapport
...
methods
function t = table(obj)
t = obj.t_;
end
function r = eq(obj1,obj2)
r = isequaln(table(obj1), table(obj2));
end
function ind = size(obj, varargin)
ind = size(table(obj), varargin{:});
end
function ind = height(obj, varargin)
ind = height(table(obj), varargin{:});
end
function ind = width(obj, varargin)
ind = width(table(obj), varargin{:});
end
function ind = end(A,k,n)
% ind = end(A.t_,k,n);
sz = size(table(A));
if k < n
ind = sz(k);
else
ind = prod(sz(k:end));
end
end
end
end
In the case of horzcat (same principle for vertcat), it is just a matter of converting back and forth between the table and Report classes:
classdef Rapport
...
methods
function r = horzcat(obj1,varargin)
listT = cell(1, nargin);
listT{1} = table(obj1);
for k = 1:numel(varargin)
kth = varargin{k};
if isa(kth, 'Report')
listT{k+1} = table(kth);
elseif isa(kth, 'table')
listT{k+1} = kth;
else
error('Input must be a table or a Report');
end
end
res = horzcat(listT{:});
r = Report(res);
end
end
end
Adding a new method
The plus operator already exists for the table class and works when the table contains all numeric values. It sums columns as long as the tables have the same length.
Something I think would be nice would be to be able to write t1 + t2, and that would perform an outerjoin operation between the tables and any sizes having similar indexing columns.
That would be so concise, and that's what we’re going to implement for the Report class as an example. That is called “plus operator overloading”. Of course, you could imagine that the “+” operator is used to compute something else, for example adding columns together with regard to the keys index. That depends on your needs.
Here’s a unittest example:
classdef ReportTest < matlab.unittest.TestCase
methods (Test)
function testPlusOperatorOverload(testCase)
t1 = array2table( ...
{ 'Smith', 'Male' ...
; 'JACKSON', 'Male' ...
; 'Williams', 'Female' ...
} , 'VariableNames', {'LastName' 'Gender'} ...
);
t2 = array2table( ...
{ 'Smith', 13 ...
; 'Williams', 6 ...
; 'JACKSON', 4 ...
}, 'VariableNames', {'LastName' 'Age'} ...
);
r1 = Report(t1);
r2 = Report(t2);
tRes = r1 + r2;
tExpected = Report( array2table( ...
{ 'JACKSON' , 'Male', 4 ...
; 'Smith' , 'Male', 13 ...
; 'Williams', 'Female', 6 ...
} , 'VariableNames', {'LastName' 'Gender' 'Age'} ...
) );
testCase.verifyEqual(tRes, tExpected);
end
end
end
And here’s how I’d implement the plus operator in the Report class definition, so that it also works if I add a table and a Report:
classdef Rapport
...
methods
function r = plus(obj1,obj2)
table1 = table(obj1);
table2 = table(obj2);
result = outerjoin(table1, table2 ...
, 'Type', 'full', 'MergeKeys', true);
r = reportingits.dom.Rapport(result);
end
end
end
The case of the subsref method
If we wish to access the elements of an instance the same way we would with regular tables, whether with parentheses, curly braces or directly with the name of the column, we need to implement the subsref and subsasgn methods. The second one, subsasgn is pretty easy, but subsref is a bit tricky, because we need to detect whether we’re directing towards existing methods or not.
Here’s the code:
classdef Rapport
...
methods
function A = subsasgn(A,S,B)
A.t_ = subsasgn(A.t_,S,B);
end
function B = subsref(A,S)
isTableMethod = @(m) ismember(m, methods('table'));
isReportMethod = @(m) ismember(m, methods('Report'));
switch true
case strcmp(S(1).type, '.') && isReportMethod(S(1).subs)
methodName = S(1).subs;
B = A.(methodName)(S(2).subs{:});
if numel(S) > 2
B = subsref(B, S(3:end));
end
case strcmp(S(1).type, '.') && isTableMethod (S(1).subs)
methodName = S(1).subs;
if ~isReportMethod(methodName)
error('The method "%s" needs to be implemented!', methodName)
end
otherwise
B = subsref(table(A),S(1));
if istable(B)
B = Report(B);
end
if numel(S) > 1
B = subsref(B, S(2:end));
end
end
end
end
end
Conclusion
I believe that the table class is Sealed because is case new methods are introduced in MATLAB in the future, the subclass might not be compatible if we created any or generate unexpected complexity.
The table class is a really powerful feature.
I hope this example has shown you how it is possible to extend the use of tables by adding new functionalities and maybe given you some ideas to simplify some usages. I’ve only happened to find it useful in very restricted cases, but was still happy to be able to do so.
In case you need to add other methods of the table class, you can see the list simply by calling methods(’table’).
Feel free to share your thoughts or any questions you might have! Maybe you’ll decide that doing so is a bad idea in the end and opt for another solution.
I thought it would be fun to vibe code Christmas trees.
Model: Claude Sonnet4.5
Prompt: Write a MATLAB script that draws a Christmas tree. There should be decorations and presents too.
Result:
christmasTree()
function christmasTree()
% Christmas Tree with Decorations and Presents
% Creates a festive scene with a decorated tree and gift boxes
figure('Color', 'w', 'Position', [100, 100, 800, 900]);
hold on;
axis equal;
axis off;
xlim([-3, 3]);
ylim([0, 10]);
% Draw the tree (three layered triangular sections)
drawTreeSection(0, 2, 2.5, 2.5, [0.1, 0.5, 0.1]);
drawTreeSection(0, 3.5, 2, 2, [0.15, 0.55, 0.15]);
drawTreeSection(0, 4.8, 1.5, 1.8, [0.2, 0.6, 0.2]);
% Tree trunk
rectangle('Position', [-0.3, 0, 0.6, 2], 'FaceColor', [0.4, 0.2, 0.1], ...
'EdgeColor', 'none');
% Add decorations
addOrnaments();
addTinsel();
% Star on top
drawStar(0, 7.2, 0.4, [1, 0.84, 0]);
% Add presents under the tree
drawPresent(-1.8, 0, 0.6, 0.5, [0.8, 0.1, 0.1], [1, 0.84, 0]);
drawPresent(-0.8, 0, 0.5, 0.6, [0.1, 0.3, 0.8], [0.9, 0.9, 0.9]);
drawPresent(1.2, 0, 0.7, 0.4, [0.7, 0.5, 0.9], [0.2, 0.8, 0.2]);
drawPresent(0.2, 0, 0.4, 0.5, [1, 0.7, 0.1], [0.8, 0.1, 0.1]);
% Add some snow on the ground
scatter(randn(1, 100)*2.5, rand(1, 100)*0.3, 20, 'w', 'filled', ...
'MarkerEdgeColor', [0.8, 0.8, 0.8]);
title('Merry Christmas!', 'FontSize', 24, 'Color', [0.8, 0.1, 0.1], ...
'FontWeight', 'bold');
hold off;
end
function drawTreeSection(x, y, width, height, color)
% Draw a triangular section of the tree
xPoints = [x - width, x + width, x];
yPoints = [y, y, y + height];
fill(xPoints, yPoints, color, 'EdgeColor', [0.05, 0.3, 0.05], ...
'LineWidth', 1.5);
end
function addOrnaments()
% Add colorful baubles to the tree
ornamentColors = [
1, 0, 0; % Red
0, 0, 1; % Blue
1, 0.84, 0; % Gold
0.9, 0.1, 0.5;% Pink
0.5, 0, 0.5 % Purple
];
% Ornament positions (x, y coordinates)
positions = [
-1.5, 2.5; 1.5, 2.5; 0, 3.2;
-1.2, 3.8; 1.2, 3.8; -0.6, 4.2; 0.6, 4.2;
-0.8, 5.2; 0.8, 5.2; 0, 5.8; -0.4, 6.3; 0.4, 6.3
];
for i = 1:size(positions, 1)
colorIdx = mod(i-1, size(ornamentColors, 1)) + 1;
x = positions(i, 1);
y = positions(i, 2);
% Draw bauble
theta = linspace(0, 2*pi, 50);
radius = 0.15;
xCirc = x + radius * cos(theta);
yCirc = y + radius * sin(theta);
fill(xCirc, yCirc, ornamentColors(colorIdx, :), ...
'EdgeColor', ornamentColors(colorIdx, :)*0.7, 'LineWidth', 1.5);
% Add highlight for shine
highlightX = x - radius*0.4 + radius*0.3*cos(theta(1:15));
highlightY = y + radius*0.4 + radius*0.3*sin(theta(1:15));
fill(highlightX, highlightY, [1, 1, 1], 'EdgeColor', 'none', ...
'FaceAlpha', 0.6);
end
end
function addTinsel()
% Add sparkly tinsel effect
tinselX = [-1.8, -1.2, -0.5, 0.2, 0.9, 1.6];
tinselY = [2.8, 3.5, 4.0, 4.5, 5.0, 5.5];
for i = 1:length(tinselX)
plot(tinselX(i) + randn(1, 5)*0.1, tinselY(i) + rand(1, 5)*0.2, ...
'*', 'Color', [1, 0.84, 0], 'MarkerSize', 8, 'LineWidth', 1.5);
end
end
function drawStar(x, y, size, color)
% Draw a 5-pointed star on top of the tree
angles = linspace(0, 2*pi, 11);
radii = repmat([size, size*0.4], 1, 5);
radii = [radii, radii(1)];
xStar = x + radii .* cos(angles - pi/2);
yStar = y + radii .* sin(angles - pi/2);
fill(xStar, yStar, color, 'EdgeColor', [0.8, 0.6, 0], 'LineWidth', 2);
% Add sparkle
plot(x, y, '*', 'Color', [1, 1, 1], 'MarkerSize', 15, 'LineWidth', 2);
end
function drawPresent(x, y, width, height, boxColor, ribbonColor)
% Draw a gift box with ribbon and bow
% Box
rectangle('Position', [x, y, width, height], 'FaceColor', boxColor, ...
'EdgeColor', boxColor*0.7, 'LineWidth', 2);
% Vertical ribbon
ribbonWidth = width * 0.15;
rectangle('Position', [x + width/2 - ribbonWidth/2, y, ribbonWidth, height], ...
'FaceColor', ribbonColor, 'EdgeColor', 'none');
% Horizontal ribbon
ribbonHeight = height * 0.15;
rectangle('Position', [x, y + height/2 - ribbonHeight/2, width, ribbonHeight], ...
'FaceColor', ribbonColor, 'EdgeColor', 'none');
% Bow on top
bowX = x + width/2;
bowY = y + height;
bowSize = width * 0.2;
% Left loop
theta = linspace(0, pi, 30);
fill(bowX - bowSize*0.3 + bowSize*0.5*cos(theta), ...
bowY + bowSize*0.5*sin(theta), ribbonColor, 'EdgeColor', 'none');
% Right loop
fill(bowX + bowSize*0.3 + bowSize*0.5*cos(theta), ...
bowY + bowSize*0.5*sin(theta), ribbonColor, 'EdgeColor', 'none');
% Center knot
theta = linspace(0, 2*pi, 30);
fill(bowX + bowSize*0.25*cos(theta), bowY + bowSize*0.25*sin(theta), ...
ribbonColor*0.8, 'EdgeColor', 'none');
end
I like this quote, what do you think?
"If the part of programming you enjoy most is the physical act of writing code, then agents will feel beside the point. You’re already where you want to be, even just with some Copilot or Cursor-style intelligent code auto completion, which makes you faster while still leaving you fully in the driver’s seat about the code that gets written.
But if the part you care about is the decision-making around the code, agents feel like they clear space. They take care of the mechanical expression and leave you with judgment, tradeoffs, and intent. Because truly, for someone at my experience level, that is my core value offering anyway. When I spend time actually typing code these days with my own fingers, it feels like a waste of my time."
— Obie Fernandez, What happens when the coding becomes the least interesting part of the work
I can't believe someone put time into this ;-)

In a recent blog post, @Guy Rouleau writes about the new Simulink Copilot Beta. Sign ups are on the Copilot Beta page below. Let him know what you think.
Guy's Blog Post - https://blogs.mathworks.com/simulink/2025/12/01/a-copilot-for-simulink/
Simulink Copilot Beta - https://www.mathworks.com/products/simulink-copilot.html

The formula comes from @yuruyurau. (https://x.com/yuruyurau)
digital life 1

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:2e4;
x = mod(i, 100);
y = floor(i./100);
k = x./4 - 12.5;
e = y./9 + 5;
o = vecnorm([k; e])./9;
while true
t = t + pi/90;
q = x + 99 + tan(1./k) + o.*k.*(cos(e.*9)./4 + cos(y./2)).*sin(o.*4 - t);
c = o.*e./30 - t./8;
SHdl.XData = (q.*0.7.*sin(c)) + 9.*cos(y./19 + t) + 200;
SHdl.YData = 200 + (q./2.*cos(c));
drawnow
end
digital life 2

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = i;
y = i./235;
e = y./8 - 13;
while true
t = t + pi/240;
k = (4 + sin(y.*2 - t).*3).*cos(x./29);
d = vecnorm([k; e]);
q = 3.*sin(k.*2) + 0.3./k + sin(y./25).*k.*(9 + 4.*sin(e.*9 - d.*3 + t.*2));
SHdl.XData = q + 30.*cos(d - t) + 200;
SHdl.YData = 620 - q.*sin(d - t) - d.*39;
drawnow
end
digital life 3

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = mod(i, 200);
y = i./43;
k = 5.*cos(x./14).*cos(y./30);
e = y./8 - 13;
d = (k.^2 + e.^2)./59 + 4;
a = atan2(k, e);
while true
t = t + pi/20;
q = 60 - 3.*sin(a.*e) + k.*(3 + 4./d.*sin(d.^2 - t.*2));
c = d./2 + e./99 - t./18;
SHdl.XData = q.*sin(c) + 200;
SHdl.YData = (q + d.*9).*cos(c) + 200;
drawnow; pause(1e-2)
end
digital life 4

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:4e4;
x = mod(i, 200);
y = i./200;
k = x./8 - 12.5;
e = y./8 - 12.5;
o = (k.^2 + e.^2)./169;
d = .5 + 5.*cos(o);
while true
t = t + pi/120;
SHdl.XData = x + d.*k.*sin(d.*2 + o + t) + e.*cos(e + t) + 100;
SHdl.YData = y./4 - o.*135 + d.*6.*cos(d.*3 + o.*9 + t) + 275;
SHdl.CData = ((d.*sin(k).*sin(t.*4 + e)).^2).'.*[1,1,1];
drawnow;
end
digital life 5

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w',...
'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = mod(i, 200);
y = i./55;
k = 9.*cos(x./8);
e = y./8 - 12.5;
while true
t = t + pi/120;
d = (k.^2 + e.^2)./99 + sin(t)./6 + .5;
q = 99 - e.*sin(atan2(k, e).*7)./d + k.*(3 + cos(d.^2 - t).*2);
c = d./2 + e./69 - t./16;
SHdl.XData = q.*sin(c) + 200;
SHdl.YData = (q + 19.*d).*cos(c) + 200;
drawnow;
end
digital life 6

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 1:1e4;
y = i./790;
k = y; idx = y < 5;
k(idx) = 6 + sin(bitxor(floor(y(idx)), 1)).*6;
k(~idx) = 4 + cos(y(~idx));
while true
t = t + pi/90;
d = sqrt((k.*cos(i + t./4)).^2 + (y/3-13).^2);
q = y.*k.*cos(i + t./4)./5.*(2 + sin(d.*2 + y - t.*4));
c = d./3 - t./2 + mod(i, 2);
SHdl.XData = q + 90.*cos(c) + 200;
SHdl.YData = 400 - (q.*sin(c) + d.*29 - 170);
drawnow; pause(1e-2)
end
digital life 7

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 1:1e4;
y = i./345;
x = y; idx = y < 11;
x(idx) = 6 + sin(bitxor(floor(x(idx)), 8))*6;
x(~idx) = x(~idx)./5 + cos(x(~idx)./2);
e = y./7 - 13;
while true
t = t + pi/120;
k = x.*cos(i - t./4);
d = sqrt(k.^2 + e.^2) + sin(e./4 + t)./2;
q = y.*k./d.*(3 + sin(d.*2 + y./2 - t.*4));
c = d./2 + 1 - t./2;
SHdl.XData = q + 60.*cos(c) + 200;
SHdl.YData = 400 - (q.*sin(c) + d.*29 - 170);
drawnow; pause(5e-3)
end
digital life 8

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl{6} = [];
for j = 1:6
SHdl{j} = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.3);
end
t = 0;
i = 1:2e4;
k = mod(i, 25) - 12;
e = i./800; m = 200;
theta = pi/3;
R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
while true
t = t + pi/240;
d = 7.*cos(sqrt(k.^2 + e.^2)./3 + t./2);
XY = [k.*4 + d.*k.*sin(d + e./9 + t);
e.*2 - d.*9 - d.*9.*cos(d + t)];
for j = 1:6
XY = R*XY;
SHdl{j}.XData = XY(1,:) + m;
SHdl{j}.YData = XY(2,:) + m;
end
drawnow;
end
digital life 9

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl{14} = [];
for j = 1:14
SHdl{j} = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.1);
end
t = 0;
i = 1:2e4;
k = mod(i, 50) - 25;
e = i./1100; m = 200;
theta = pi/7;
R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
while true
t = t + pi/240;
d = 5.*cos(sqrt(k.^2 + e.^2) - t + mod(i, 2));
XY = [k + k.*d./6.*sin(d + e./3 + t);
90 + e.*d - e./d.*2.*cos(d + t)];
for j = 1:14
XY = R*XY;
SHdl{j}.XData = XY(1,:) + m;
SHdl{j}.YData = XY(2,:) + m;
end
drawnow;
end
If you haven't solved the problem yet, below hints guide how the algorithm should be implemented and clarify subtle rules that are easy to miss.
1. Shield is ONLY defended in HOME matches of the CURRENT holder - Even if a team beats the Shield holder in an away match, that does NOT count as a Shield defense.
2. A team defends the Shield ONLY when:
> They currently hold it.
> They are home team in that match
3. Shield transfer happens ONLY if the HOLDER plays a home match AND loses - A team may lose an away match — no effect.
4. The output ALWAYS includes the initial holder as the first row.
5. Defenses count resets for each new holder. - Every holder accumulates their own count until they lose it at home.
6. Match numbers are 1-indexed in the input, but “0” is used for initial state - The first real match is Match 1, but the output starts with Match 0.
7. Output row is created ONLY WHEN SHIELD CHANGES HANDS - This is an important hidden detail. A new row is appended, When the current holder loses a home match → Shield taken by visitor. If no loss at home occurs after that → no new row until next change.
8. The last holder’s defense count goes until the season ends - Even if they lose away later.
9. If a holder never gets a home match, defenses = 0.
10. In case the holder loses their very first home match → defenses = 0.
11. Shield changes only on HOME LOSS, not on a draw.
I hope above hints will help you in solving the problem.
Thanks and Regards,
Dev

% Recreation of Saturn photo
figure('Color', 'k', 'Position', [100, 100, 800, 800]);
ax = axes('Color', 'k', 'XColor', 'none', 'YColor', 'none', 'ZColor', 'none');
hold on;
% Create the planet sphere
[x, y, z] = sphere(150);
% Saturn colors - pale yellow/cream gradient
saturn_radius = 1;
% Create color data based on latitude for gradient effect
lat = asin(z);
color_data = rescale(lat, 0.3, 0.9);
% Plot Saturn with smooth shading
planet = surf(x*saturn_radius, y*saturn_radius, z*saturn_radius, ...
color_data, ...
'EdgeColor', 'none', ...
'FaceColor', 'interp', ...
'FaceLighting', 'gouraud', ...
'AmbientStrength', 0.3, ...
'DiffuseStrength', 0.6, ...
'SpecularStrength', 0.1);
% Use a cream/pale yellow colormap for Saturn
cream_map = [linspace(0.4, 0.95, 256)', ...
linspace(0.35, 0.9, 256)', ...
linspace(0.2, 0.7, 256)'];
colormap(cream_map);
% Create the ring system
n_points = 300;
theta = linspace(0, 2*pi, n_points);
% Define ring structure (inner radius, outer radius, brightness)
rings = [
1.2, 1.4, 0.7; % Inner ring
1.45, 1.65, 0.8; % A ring
1.7, 1.85, 0.5; % Cassini division (darker)
1.9, 2.3, 0.9; % B ring (brightest)
2.35, 2.5, 0.6; % C ring
2.55, 2.8, 0.4; % Outer rings (fainter)
];
% Create rings as patches
for i = 1:size(rings, 1)
r_inner = rings(i, 1);
r_outer = rings(i, 2);
brightness = rings(i, 3);
% Create ring coordinates
x_inner = r_inner * cos(theta);
y_inner = r_inner * sin(theta);
x_outer = r_outer * cos(theta);
y_outer = r_outer * sin(theta);
% Front side of rings
ring_x = [x_inner, fliplr(x_outer)];
ring_y = [y_inner, fliplr(y_outer)];
ring_z = zeros(size(ring_x));
% Color based on brightness
ring_color = brightness * [0.9, 0.85, 0.7];
fill3(ring_x, ring_y, ring_z, ring_color, ...
'EdgeColor', 'none', ...
'FaceAlpha', 0.7, ...
'FaceLighting', 'gouraud', ...
'AmbientStrength', 0.5);
end
% Add some texture/gaps in the rings using scatter
n_particles = 3000;
r_particles = 1.2 + rand(1, n_particles) * 1.6;
theta_particles = rand(1, n_particles) * 2 * pi;
x_particles = r_particles .* cos(theta_particles);
y_particles = r_particles .* sin(theta_particles);
z_particles = (rand(1, n_particles) - 0.5) * 0.02;
% Vary particle brightness
particle_colors = repmat([0.8, 0.75, 0.6], n_particles, 1) .* ...
(0.5 + 0.5*rand(n_particles, 1));
scatter3(x_particles, y_particles, z_particles, 1, particle_colors, ...
'filled', 'MarkerFaceAlpha', 0.3);
% Add dramatic outer halo effect - multiple layers extending far out
n_glow = 20;
for i = 1:n_glow
glow_radius = 1 + i*0.35; % Extend much farther
alpha_val = 0.08 / sqrt(i); % More visible, slower falloff
% Color gradient from cream to blue/purple at outer edges
if i <= 8
glow_color = [0.9, 0.85, 0.7]; % Warm cream/yellow
else
% Gradually shift to cooler colors
mix = (i - 8) / (n_glow - 8);
glow_color = (1-mix)*[0.9, 0.85, 0.7] + mix*[0.6, 0.65, 0.85];
end
surf(x*glow_radius, y*glow_radius, z*glow_radius, ...
ones(size(x)), ...
'EdgeColor', 'none', ...
'FaceColor', glow_color, ...
'FaceAlpha', alpha_val, ...
'FaceLighting', 'none');
end
% Add extensive glow to rings - make it much more dramatic
n_ring_glow = 12;
for i = 1:n_ring_glow
glow_scale = 1 + i*0.15; % Extend farther
alpha_ring = 0.12 / sqrt(i); % More visible
for j = 1:size(rings, 1)
r_inner = rings(j, 1) * glow_scale;
r_outer = rings(j, 2) * glow_scale;
brightness = rings(j, 3) * 0.5 / sqrt(i);
x_inner = r_inner * cos(theta);
y_inner = r_inner * sin(theta);
x_outer = r_outer * cos(theta);
y_outer = r_outer * sin(theta);
ring_x = [x_inner, fliplr(x_outer)];
ring_y = [y_inner, fliplr(y_outer)];
ring_z = zeros(size(ring_x));
% Color gradient for ring glow
if i <= 6
ring_color = brightness * [0.9, 0.85, 0.7];
else
mix = (i - 6) / (n_ring_glow - 6);
ring_color = brightness * ((1-mix)*[0.9, 0.85, 0.7] + mix*[0.65, 0.7, 0.9]);
end
fill3(ring_x, ring_y, ring_z, ring_color, ...
'EdgeColor', 'none', ...
'FaceAlpha', alpha_ring, ...
'FaceLighting', 'none');
end
end
% Add diffuse glow particles for atmospheric effect
n_glow_particles = 8000;
glow_radius_particles = 1.5 + rand(1, n_glow_particles) * 5;
theta_glow = rand(1, n_glow_particles) * 2 * pi;
phi_glow = acos(2*rand(1, n_glow_particles) - 1);
x_glow = glow_radius_particles .* sin(phi_glow) .* cos(theta_glow);
y_glow = glow_radius_particles .* sin(phi_glow) .* sin(theta_glow);
z_glow = glow_radius_particles .* cos(phi_glow);
% Color particles based on distance - cooler colors farther out
particle_glow_colors = zeros(n_glow_particles, 3);
for i = 1:n_glow_particles
dist = glow_radius_particles(i);
if dist < 3
particle_glow_colors(i,:) = [0.9, 0.85, 0.7];
else
mix = (dist - 3) / 4;
particle_glow_colors(i,:) = (1-mix)*[0.9, 0.85, 0.7] + mix*[0.5, 0.6, 0.9];
end
end
scatter3(x_glow, y_glow, z_glow, rand(1, n_glow_particles)*2+0.5, ...
particle_glow_colors, 'filled', 'MarkerFaceAlpha', 0.05);
% Lighting setup
light('Position', [-3, -2, 4], 'Style', 'infinite', ...
'Color', [1, 1, 0.95]);
light('Position', [2, 3, 2], 'Style', 'infinite', ...
'Color', [0.3, 0.3, 0.4]);
% Camera and view settings
axis equal off;
view([-35, 25]); % Angle to match saturn_photo.jpg - more dramatic tilt
camva(10); % Field of view - slightly wider to show full halo
xlim([-8, 8]); % Expanded to show outer halo
ylim([-8, 8]);
zlim([-8, 8]);
% Material properties
material dull;
title('Saturn - Left click: Rotate | Right click: Pan | Scroll: Zoom', 'Color', 'w', 'FontSize', 12);
% Enable interactive camera controls
cameratoolbar('Show');
cameratoolbar('SetMode', 'orbit'); % Start in rotation mode
% Custom mouse controls
set(gcf, 'WindowButtonDownFcn', @mouseDown);
function mouseDown(src, ~)
selType = get(src, 'SelectionType');
switch selType
case 'normal' % Left click - rotate
cameratoolbar('SetMode', 'orbit');
rotate3d on;
case 'alt' % Right click - pan
cameratoolbar('SetMode', 'pan');
pan on;
end
end
Many MATLAB Cody problems involve solving congruences, modular inverses, Diophantine equations, or simplifying ratios under constraints. A powerful tool for these tasks is the Extended Euclidean Algorithm (EEA), which not only computes the greatest common divisor, gcd(a,b), but also provides integers x and y such that: a*x + b*y = gcd(a,b) - which is Bezout's identity.
Use of the Extended Euclidean Algorithm is very using in solving many different types of MATLAB Cody problems such as:
- Computing modular inverses safely, even for very large numbers
- Solving linear Diophantine equations
- Simplifing fractions or finding nteger coefficients without using symbolic tools
- Avoiding loops (EEA can be implemented recursively)
Below is a recursive implementation of the EEA.
function [g,x,y] = egcd(a,b)
% a*x + b*y = g [gcd(a,b)]
if b == 0
g = a; x = 1; y = 0;
else
[g, x1, y1] = egcd(b, mod(a,b));
x = y1;
y = x1 - floor(a/b)*y1;
end
end
Problem:
Given integers a and m, return the modular inverse of a (mod m).
If the inverse does not exist, return -1.
function inv = modInverse(a,m)
[g,x,~] = egcd(a,m);
if g ~= 1 % inverse doesn't exist
inv = -1;
else
inv = mod(x,m); % Bézout coefficient gives the inverse
end
end
%find the modular inverse of 19 (mod 5)
inv=modInverse(19,5)
Congratulations to all the Relentless Coders who have completed the problem set. I hope you weren't too busy relentlessly solving problems to enjoy the silliness I put into them.
If you've solved the whole problem set, don't forget to help out your teammates with suggestions, tips, tricks, etc. But also, just for fun, I'm curious to see which of my many in-jokes and nerdy references you noticed. Many of the problems were inspired by things in the real world, then ported over into the chaotic fantasy world of Nedland.
I guess I'll start with the obvious real-world reference: @Ned Gulley (I make no comment about his role as insane despot in any universe, real or otherwise.)
Hi Everyone!
As this is the most difficult question in problem group "Cody Contest 2025". To solve this problem, It is very important to understand all the hidden clues in the problem statement. Because everything is not directly visible.
For those who tried the problem, but were not able to solve. You might have missed any of the below hints -
- “The other players do not get to see which card has been shown, but they do know which three cards were asked for and that the player asked had one of them.” - Even when the card identity isn’t revealed (result = 0), you still gain partial knowledge — the asked player must have at least one of those three cards, meaning you can mark other players as not having all three simultaneously.
- "If it is your turn, you know the exact identity of that card" - You only know the exact shown card when result = 1, 2, or 3 — and it must be your turn. If someone else asked (even if you know result = 0), you don’t know which one was shown. So the meaning of result depends on whose turn it was, which is implicit — MATLAB code must assume that turns alternate 1→m→1, so your turn index is determined by (t-1) mod m + 1 == pnum.
- "Any leftover cards are placed face-up so that all players can see them" - These cards (commoncards) are not in anyone’s hand and cannot be in the envelope. So they’re not just visible — they’re logical constraints to eliminate from deduction.
- “It may be possible to determine the solution from less information than is given, but the information given will always be sufficient.”
- "Turn order is implied, not given explicitly" - Players take turns in order (1 to m, and back to 1).
On considering all the clues and constraints in the question, you will definitely be able to card for each category present in envelope.
I hope above clues will be useful for you.
Thank you, wishing you the success!
Regards,
Dev
Experimenting with Agentic AI
44%
I am an AI skeptic
0%
AI is banned at work
11%
I am happy with Conversational AI
44%
9 votes
When solving Cody problems, sometimes your solution takes too long — especially if you’re recomputing large arrays or iterative sequences every time your function is called.
The Cody work area resets between separate runs of your code, but within one Cody test suite, your function may be called multiple times in a single session.
This is where persistent variables come in handy.
A persistent variable keeps its value between function calls, but only while MATLAB is still running your function suite.
This means:
- You can cache results to avoid recomputation.
- You can accumulate data across multiple calls.
- But it resets when Cody or MATLAB restarts.
Suppose you’re asked to find the n-th Fibonacci number efficiently — Cody may time out if you use recursion naively. Here’s how to use persistent to store computed values:
function f = fibPersistent(n)
import java.math.BigInteger
persistent F
if isempty(F)
F=[BigInteger('0'),BigInteger('1')];
for k=3:10000
F(k)=F(k-1).add(F(k-2));
end
end
% Extend the stored sequence only if needed
while length(F) <= n
F(end+1)=F(end).add(F(end-1));
end
f = char(F(n+1).toString); % since F(1) is really F(0)
end
%calling function 100 times
K=arrayfun(@(x)fibPersistent(x),randi(10000,1,100),'UniformOutput',false);
K(100)
The fzero function can handle extremely messy equations — even those mixing exponentials, trigonometric, and logarithmic terms — provided the function is continuous near the root and you give a reasonable starting point or interval.
It’s ideal for cases like:
- Solving energy balance equations
- Finding intersection points of nonlinear models
- Determining parameters from experimental data
Example: Solving for Equilibrium Temperature in a Heat Radiation-Conduction Model
Suppose a spacecraft component exchanges heat via conduction and radiation with its environment. At steady state, the power generated internally equals the heat lost:
Given constants:
 = 25 W
= 25 W- k = 0.5 W/K
- ϵ = 0.8
- σ = 5.67e−8 W/m²K⁴
- A = 0.1 m²
 = 250 K
= 250 K
Find the steady-state temperature, T.
% Given constants
Qgen = 25;
k = 0.5;
eps = 0.8;
sigma = 5.67e-8;
A = 0.1;
Tinf = 250;
% Define the energy balance equation (set equal to zero)
f = @(T) Qgen - (k*(T - Tinf) + eps*sigma*A*(T.^4 - Tinf^4));
% Plot for a sense of where the root lies before implementing
fplot(f, [250 300]); grid on
xlabel('Temperature (K)'); ylabel('f(T)')
title('Energy Balance: Root corresponds to steady-state temperature')
% Use fzero with an interval that brackets the root
T_eq = fzero(f, [250 300]);
fprintf('Steady-state temperature: %.2f K\n', T_eq);

It’s exciting to dive into a new dataset full of unfamiliar variables but it can also be overwhelming if you’re not sure where to start. Recently, I discovered some new interactive features in MATLAB live scripts that make it much easier to get an overview of your data. With just a few clicks, you can display sparklines and summary statistics using table variables, sort and filter variables, and even have MATLAB generate the corresponding code for reproducibility.
The Graphics and App Building blog published an article that walks through these features showing how to explore, clean, and analyze data—all without writing any code.
If you’re interested in streamlining your exploratory data analysis or want to see what’s new in live scripts, you might find it helpful:
If you’ve tried these features or have your own tips for quick data exploration in MATLAB, I’d love to hear your thoughts!
Pure Matlab
82%
Simulink
18%
11 votes
I set my 3D matrix up with the players in the 3rd dimension. I set up the matrix with: 1) player does not hold the card (-1), player holds the card (1), and unknown holding the card (0). I moved through the turns (-1 and 1) that are fixed first. Then cycled through the conditional turns (0) while checking the cards of each player using the hints provided until it was solved. The key for me in solving several of the tests (11, 17, and 19) was looking at the 1's and 0's being held by each player.
sum(cardState==1,3);%any zeros in this 2D matrix indicate possible cards in the solution
sum(cardState==0,3)>0;%the ones in this 2D matrix indicate the only unknown positions
sum(cardState==1,3)|sum(cardState==0,3)>0;%oring the two together could provide valuable information
Some MATLAB Cody problems prohibit loops (for, while) or conditionals (if, switch, while), forcing creative solutions.
One elegant trick is to use nested functions and recursion to achieve the same logic — while staying within the rules.
Example: Recursive Summation Without Loops or Conditionals
Suppose loops and conditionals are banned, but you need to compute the sum of numbers from 1 to n. This is a simple example and obvisously n*(n+1)/2 would be preferred.
function s = sumRecursive(n)
zero=@(x)0;
s = helper(n); % call nested recursive function
function out = helper(k)
L={zero,@helper};
out = k+L{(k>0)+1}(k-1);
end
end
sumRecursive(10)
- The helper function calls itself until the base case is reached.
- Logical indexing into a cell array (k>0) act as an 'if' replacement.
- MATLAB allows nested functions to share variables and functions (zero), so you can keep state across calls.
Tips:
- Replace 'if' with logical indexing into a cell array.
- Replace for/while with recursion.
- Nested functions are local and can access outer variables, avoiding global state.


