Results for
Introduction
MCP is an open protocol that can link Claude and other AI Apps to MATLAB using MATLAB MCP Core Server (released in Nov 2025). For an introduction, see Exploring the MATLAB Model Context Protocol (MCP) Core Server with Claude Desktop. Here, I describe my experience with installation and testing Claude-Code and MATLAB, a security concern, and in particular how I "taught" Claude to handle various MATLAB file formats.
Setup
A basic installation requires you download for your operating system claude-code, matlab-mcp-core-server, and node.js. One configuration is a terminal-launched claude connected to MATLAB. To connect Claude App to MATLAB requires an alternate configuration step and I recommend it for interative use. The configuration defines the default node/folder and MATLAB APP location.
I recommend using Claude itself to guide you through the installation and configuration steps for your operating system by providing terminal commands. I append Claude’s general description of installation for my APPLE Silicon laptop. Once set up, just ask in Claude App to do something in MATLAB and MATLAB App will be launched.
Security warning: Explore the following at your own risk.
When working with Claude App, Claude code, and MATLAB, you are granting Claude AI access to read and write files. By default, you must approve (one time or forever) any action so you hopefully don’t clobber files etc. Claude App believes it can not directly access file outside the top node defined in the setup. For this reason, I set the top node to be a folder ..../Documents/MATLAB. However, Claude inherits MATLAB App's command line privileges, typically your full system privileges. Claude can describe for you some work-arounds like a Docker container which might still be license validation compatible. I have not explored such options. During my setup, Claude just provided me terminal commands to copy and run. After setup, I've demonstrated it can run system level commands via matlab:evaluate_matlab_code and the MCP server. Be careful out there!
My first test
Claude can write a text-based .m script, execute it, collect text standard output from it, and open files it makes (or any file). It cannot access figures that you might see in MATLAB App unless they are saved as files or embedded in files. As we will see, the figures generated by a Live Script are saved in an Claude-accessible format when the Live Script is saved so the code need not itself export them.
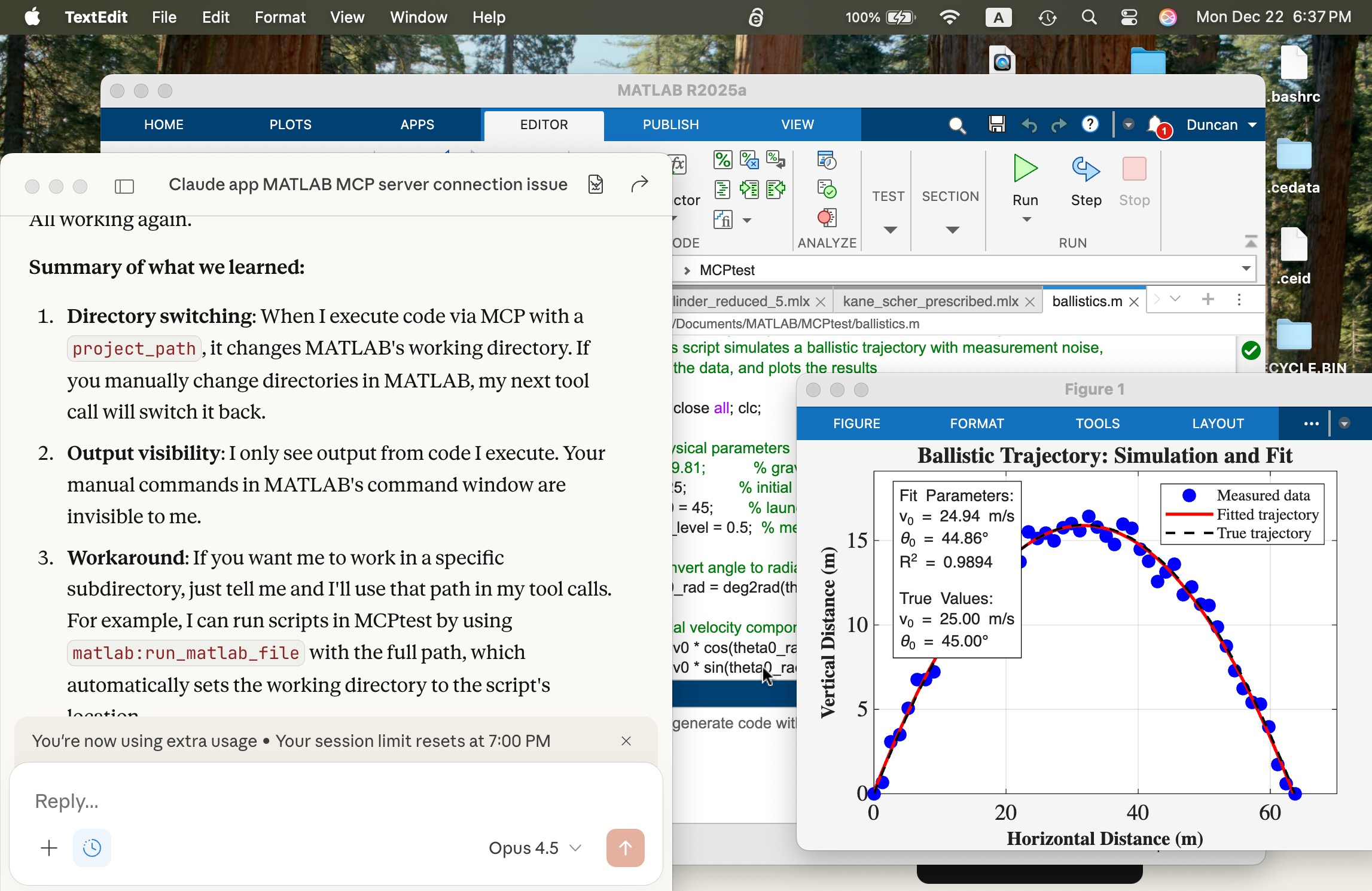
In the screen shot below, the window at left is the Claude App after a successful connection. The MATLAB App window shows a script in the MATLAB editor that simulates a ballistics experiment, the script created successfully with a terminal-interfaced Claude and a simple prompt on the first try.
I deliberately but trivially broke this script using MATLAB App interactively by commenting out a needed variable g (acceleration of gravity) and saving the script to the edit was accessible to Claude. Using Claude App after its connection, I fixed the script with a simple prompt and ran it successfully to make the figure you see. The visible MATLAB didn’t know the code had been altered and fixed by Claude until I reloaded the file. Claude recommends plots be saved in PNG or JPEG, not PDF. It can describe in detail a plot in a PNG and thusly judge if the code is functioning correctly.
Live Scripts with Claude
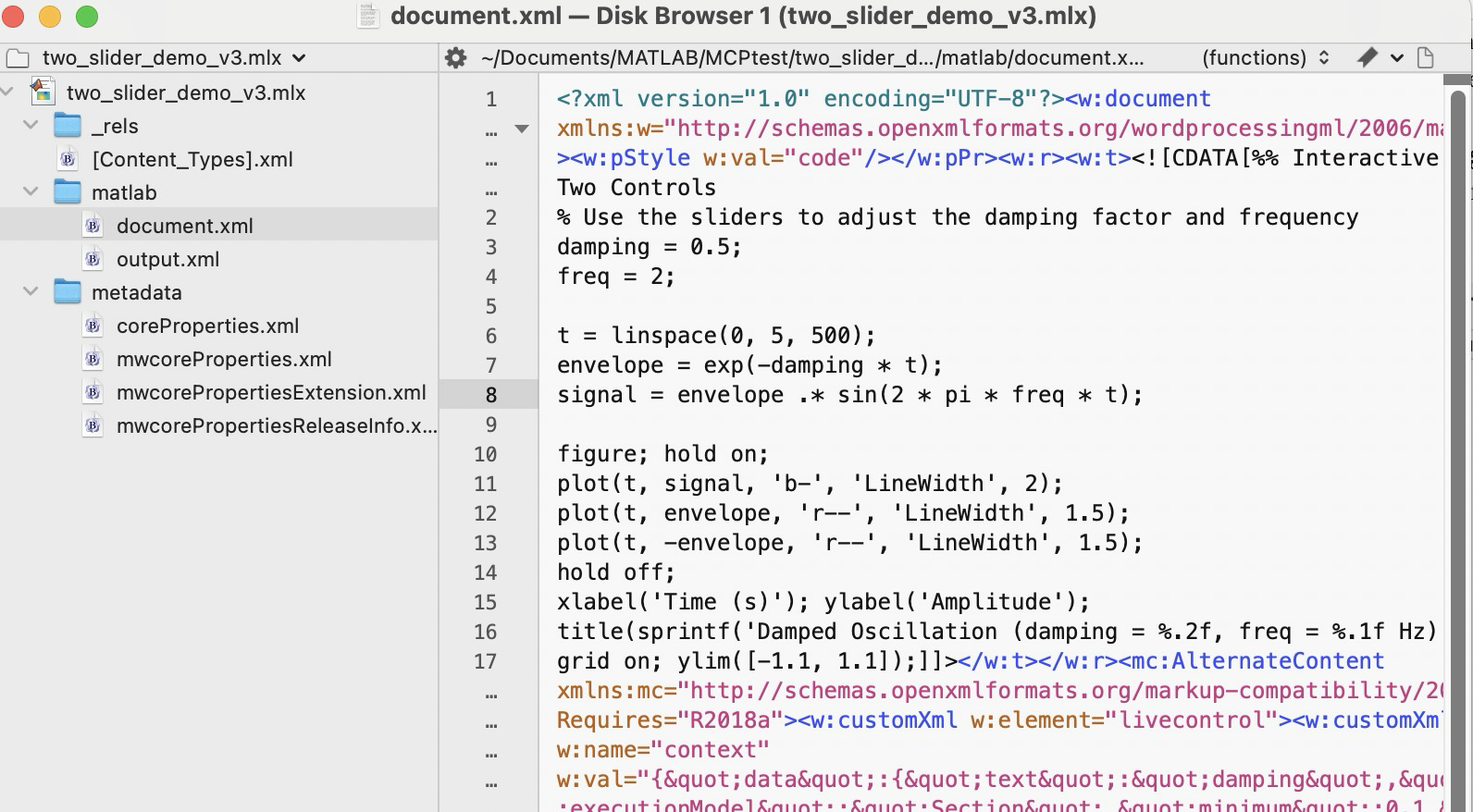
What about Live Scripts (.mlx) and the (2025a) .m live? A .mlx file is a zipped package of files mixing code and images wtih XML markup. You can peek inside one and edit it directly without unzipping and rezipping it using a tool like BBEdit on a Mac, as shown below. This short test script has two interactive slider controls. You can in v2025+ now save a .mlx in a transportable .m Live text file format. The .mlx and .m Live formats have special markup for formatted text, interactive features like sliders, and figures.
Claude can convert a vanilla .m file to .mlx using matlab.internal.liveeditor.openAndSave(source.m, dest.mlx) and the reverse matlab.internal.liveeditor.openAndConvert('myfile.mlx', 'myfile.m’).
These functions do not support .m Live yet apparently. It would be great if they did.
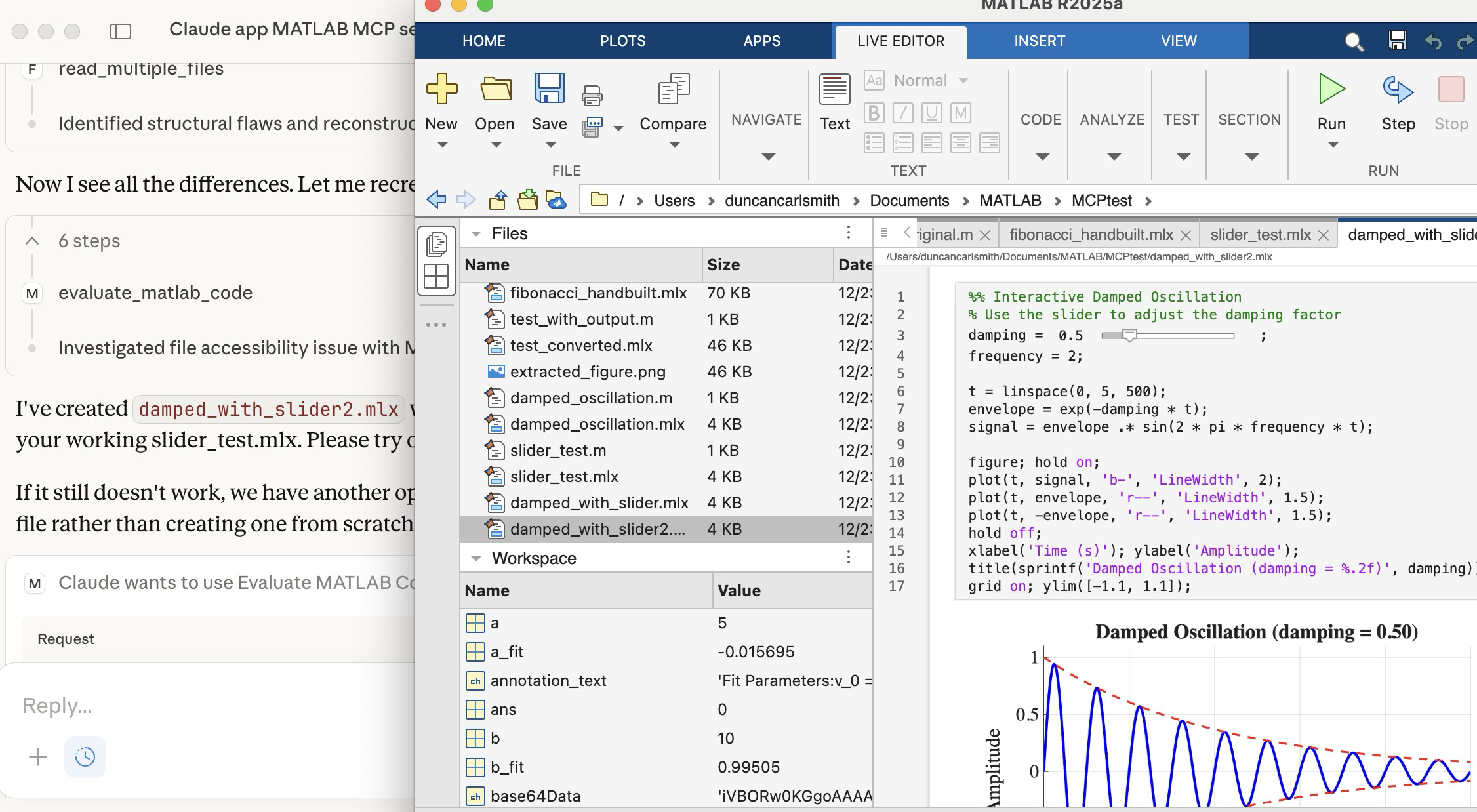
Vanilla Claude doesn’t know all the details of the .mlx and .m formats yet. To teach Claude these formats, I created a simple .mlx with interactive features (sliders), saved it, and exported it to .m Live. I then sketched for Claude these structures. Claude digested these files and was then able to create such formats from scratch immediately. Wow! In the figure below, you see Claude on the left after creating a .mlx with sliders from scratch. The successfully executed Live Script appears in the MATLAB App.
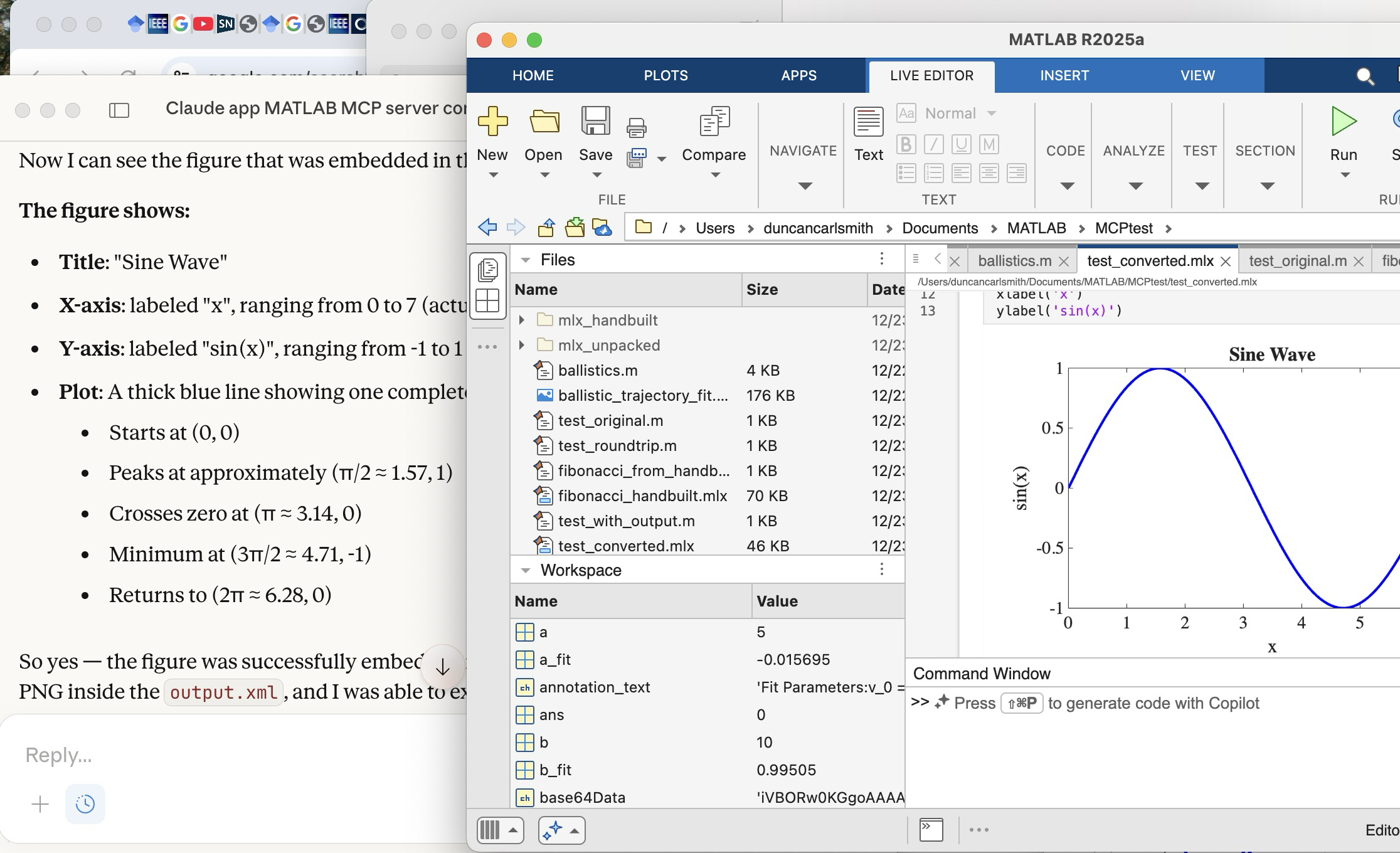
Once Claude knows the .mlx format, it can peek inside a saved .mlx, process a PNG figure saved there, and describe it, as illustrated below. Here you see Claude describing a plot it found in the .mlx shown in the MATLAB window.
Wrap up
This summarizes my first look at using claude-code. The generation of simple MATLAB codes with the latest models is increasingly trivial with Claude, Perplexity, Open.ai GPT and other apps and the direct method of code and other file transfer between a native MATLAB and Claude seems to beat a copy-paste workflow. New methods to connect MATLAB Online with commercial AI's like Comet and Anthropic's Chrome extension seem to me more fluid and intuitive in that the user and the AI are co-working the same interface without copy-paste steps, but seem slower.
Appendix
Here are installation and setup instructions for Mac from Claude for reference.
Setting Up Claude Code + MATLAB MCP Server on Mac
Part 1: Claude Code
Install via npm:
bash
npm install -g @anthropic-ai/claude-code
Or via Homebrew:
bash
brew install claude-code
Run it:
bash
cd /path/to/your/project
claude
You'll need to authenticate with your Anthropic account on first run. Claude Code works in your terminal and can read/write files, run commands, and do agentic coding tasks.
Part 2: MATLAB MCP Server
Step 1: Download the server binary
Go to the MathWorks GitHub or File Exchange and download matlab-mcp-core-server for macOS (Apple Silicon or Intel depending on your Mac).
Step 2: Make it executable
bash
chmod +x ~/Downloads/matlab-mcp-core-server
Step 3: Create/edit Claude Desktop config
Edit ~/Library/Application Support/Claude/claude_desktop_config.json:
json
{
"mcpServers": {
"matlab": {
"command": "/Users/YOURUSERNAME/Downloads/matlab-mcp-core-server",
"args": ["--matlab-root", "/Applications/MATLAB_R2025a.app"]
},
"filesystem": {
"command": "npx",
"args": [
"@modelcontextprotocol/server-filesystem",
"/Users/YOURUSERNAME/Documents/MATLAB"
]
}
}
}
Replace YOURUSERNAME with your actual username, and adjust the MATLAB version if needed.
Step 4: Install Node.js (if not already)
bash
brew install node
Step 5: Restart Claude Desktop
Quit fully (Cmd+Q) and reopen. You should see a hammer/tools icon indicating MCP servers are connected.
Part 3: Verify Connection
In Claude Desktop, ask me to run MATLAB code. I should be able to execute:
matlab
disp('Hello from MATLAB!')
Troubleshooting
Check logs:
bash
cat ~/Library/Logs/Claude/mcp-server-matlab.log
cat ~/Library/Logs/Claude/mcp.log
Common issues:
- Missing --matlab-root argument → "no valid MATLAB environments found"
Connecting Claude App to MATLAB via MCP Server
Edit ~/Library/Application Support/Claude/claude_desktop_config.json:
json
{
"mcpServers": {
"filesystem": {
"command": "npx",
"args": [
"-y",
"@modelcontextprotocol/server-filesystem",
"/Users/YOURUSERNAME/Documents/MATLAB"
]
},
"matlab": {
"command": "/Users/YOURUSERNAME/Downloads/matlab-mcp-core-server",
"args": [
"--matlab-root", "/Applications/MATLAB_R2025a.app"
]
}
}
}
Then fully quit Claude Desktop (Cmd+Q) and reopen.
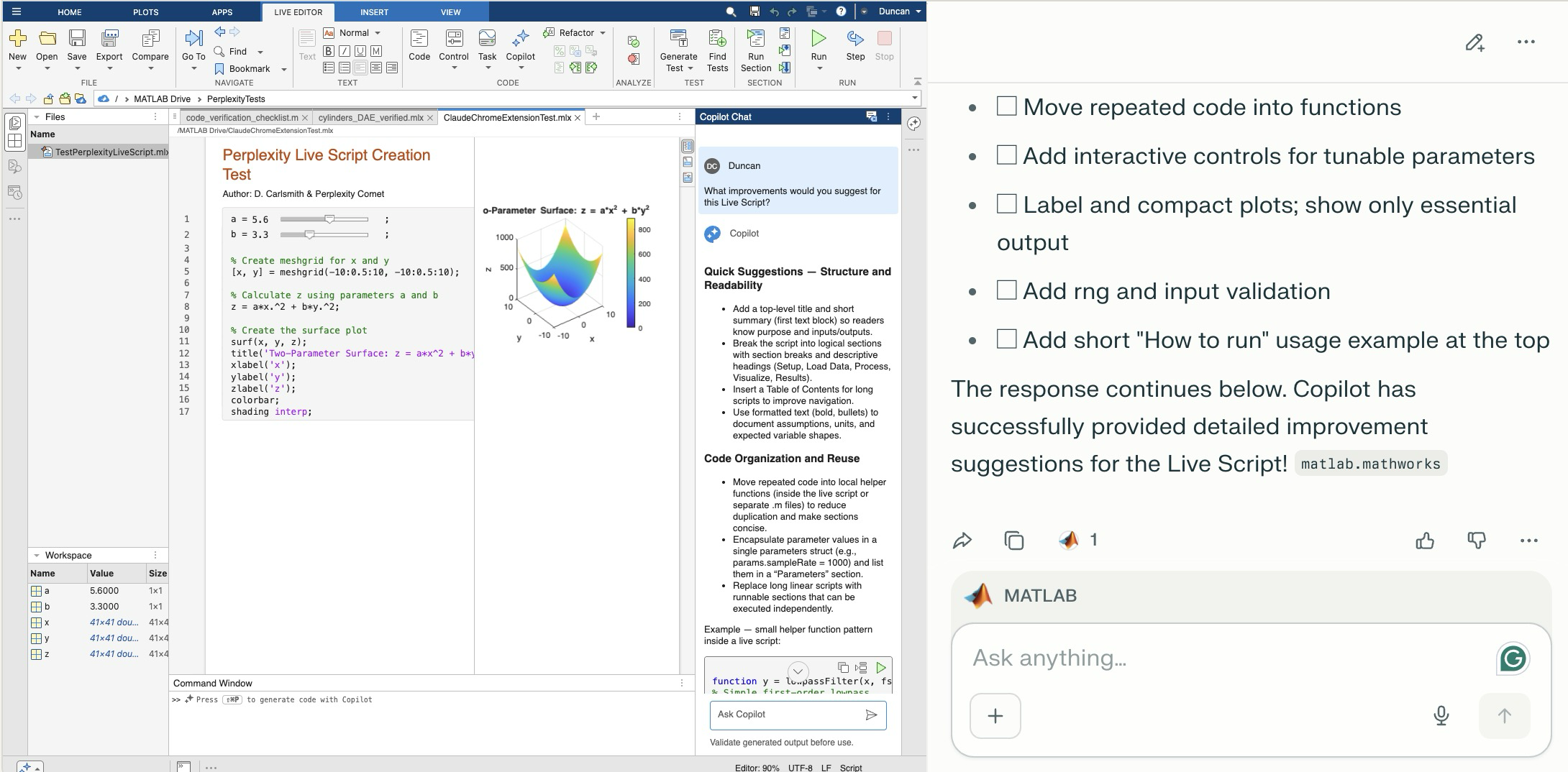
Comet browser can figure out and operate a user interface on the web including MATLAB Online. The screen shot shows MATLAB online to the left of the Comet AI. You see a test Live Script with sliders thjat Comet created in a folder (that it created). Comet is summarizing suggested improvements it requested of MATLAB Online's Copilot. Comet can plow into the arcane NASA astrophysical database interface SIMBAD, figure out how to grab information about, say, a star orbiting the black hole in the center of our galaxy and structure that information into a MATLAB data structure in a MATLAB script and run the script in MATLAB Online and display the results in the structure - it succeeded on the first try. It can do a Google Scholar citation tree search and park the results in MATLAB (success first try) or presumably in say MS Word in Office online. Presumably it can switch to a JuypterHub tab to then run a notebook or what you will. It can make mistakes, explore and discover GUI options, and recover e.g. use undo paste in MATLAB, operate in the command window, get help via the GUI if needed. Not at light speed but this seems enabling. Just released, Claude Chrome Extension Beta has similar capabilities.
Inspired in part by Christmas Trees, I'm curious about people's experience using AI to generate Matlab code.
1. Do you use AI to generate production code or just for experimentation/fun code?
2. Do you use the AI for a complete solution? Or is it more that the AI gets you most of the way there and you have to apply the finishing touches manually?
3. What level of quality would you consider the generated code? Does it follow "standard" Matlab coding practices? Is it well commented? Factored into modular functions? Argument checking? Memory efficient? Fast execution? Etc.?
4. Does the AI ever come up with a good or clever solution of which you wouldn't have thought or maybe of which you weren't even aware?
5. Is it easy/hard to express your requirements in a manner that the AI tool effectively translates into something useful?
6. Any other thoughts you'd care to share?
I thought it would be fun to vibe code Christmas trees.
Model: Claude Sonnet4.5
Prompt: Write a MATLAB script that draws a Christmas tree. There should be decorations and presents too.
Result:
christmasTree()
function christmasTree()
% Christmas Tree with Decorations and Presents
% Creates a festive scene with a decorated tree and gift boxes
figure('Color', 'w', 'Position', [100, 100, 800, 900]);
hold on;
axis equal;
axis off;
xlim([-3, 3]);
ylim([0, 10]);
% Draw the tree (three layered triangular sections)
drawTreeSection(0, 2, 2.5, 2.5, [0.1, 0.5, 0.1]);
drawTreeSection(0, 3.5, 2, 2, [0.15, 0.55, 0.15]);
drawTreeSection(0, 4.8, 1.5, 1.8, [0.2, 0.6, 0.2]);
% Tree trunk
rectangle('Position', [-0.3, 0, 0.6, 2], 'FaceColor', [0.4, 0.2, 0.1], ...
'EdgeColor', 'none');
% Add decorations
addOrnaments();
addTinsel();
% Star on top
drawStar(0, 7.2, 0.4, [1, 0.84, 0]);
% Add presents under the tree
drawPresent(-1.8, 0, 0.6, 0.5, [0.8, 0.1, 0.1], [1, 0.84, 0]);
drawPresent(-0.8, 0, 0.5, 0.6, [0.1, 0.3, 0.8], [0.9, 0.9, 0.9]);
drawPresent(1.2, 0, 0.7, 0.4, [0.7, 0.5, 0.9], [0.2, 0.8, 0.2]);
drawPresent(0.2, 0, 0.4, 0.5, [1, 0.7, 0.1], [0.8, 0.1, 0.1]);
% Add some snow on the ground
scatter(randn(1, 100)*2.5, rand(1, 100)*0.3, 20, 'w', 'filled', ...
'MarkerEdgeColor', [0.8, 0.8, 0.8]);
title('Merry Christmas!', 'FontSize', 24, 'Color', [0.8, 0.1, 0.1], ...
'FontWeight', 'bold');
hold off;
end
function drawTreeSection(x, y, width, height, color)
% Draw a triangular section of the tree
xPoints = [x - width, x + width, x];
yPoints = [y, y, y + height];
fill(xPoints, yPoints, color, 'EdgeColor', [0.05, 0.3, 0.05], ...
'LineWidth', 1.5);
end
function addOrnaments()
% Add colorful baubles to the tree
ornamentColors = [
1, 0, 0; % Red
0, 0, 1; % Blue
1, 0.84, 0; % Gold
0.9, 0.1, 0.5;% Pink
0.5, 0, 0.5 % Purple
];
% Ornament positions (x, y coordinates)
positions = [
-1.5, 2.5; 1.5, 2.5; 0, 3.2;
-1.2, 3.8; 1.2, 3.8; -0.6, 4.2; 0.6, 4.2;
-0.8, 5.2; 0.8, 5.2; 0, 5.8; -0.4, 6.3; 0.4, 6.3
];
for i = 1:size(positions, 1)
colorIdx = mod(i-1, size(ornamentColors, 1)) + 1;
x = positions(i, 1);
y = positions(i, 2);
% Draw bauble
theta = linspace(0, 2*pi, 50);
radius = 0.15;
xCirc = x + radius * cos(theta);
yCirc = y + radius * sin(theta);
fill(xCirc, yCirc, ornamentColors(colorIdx, :), ...
'EdgeColor', ornamentColors(colorIdx, :)*0.7, 'LineWidth', 1.5);
% Add highlight for shine
highlightX = x - radius*0.4 + radius*0.3*cos(theta(1:15));
highlightY = y + radius*0.4 + radius*0.3*sin(theta(1:15));
fill(highlightX, highlightY, [1, 1, 1], 'EdgeColor', 'none', ...
'FaceAlpha', 0.6);
end
end
function addTinsel()
% Add sparkly tinsel effect
tinselX = [-1.8, -1.2, -0.5, 0.2, 0.9, 1.6];
tinselY = [2.8, 3.5, 4.0, 4.5, 5.0, 5.5];
for i = 1:length(tinselX)
plot(tinselX(i) + randn(1, 5)*0.1, tinselY(i) + rand(1, 5)*0.2, ...
'*', 'Color', [1, 0.84, 0], 'MarkerSize', 8, 'LineWidth', 1.5);
end
end
function drawStar(x, y, size, color)
% Draw a 5-pointed star on top of the tree
angles = linspace(0, 2*pi, 11);
radii = repmat([size, size*0.4], 1, 5);
radii = [radii, radii(1)];
xStar = x + radii .* cos(angles - pi/2);
yStar = y + radii .* sin(angles - pi/2);
fill(xStar, yStar, color, 'EdgeColor', [0.8, 0.6, 0], 'LineWidth', 2);
% Add sparkle
plot(x, y, '*', 'Color', [1, 1, 1], 'MarkerSize', 15, 'LineWidth', 2);
end
function drawPresent(x, y, width, height, boxColor, ribbonColor)
% Draw a gift box with ribbon and bow
% Box
rectangle('Position', [x, y, width, height], 'FaceColor', boxColor, ...
'EdgeColor', boxColor*0.7, 'LineWidth', 2);
% Vertical ribbon
ribbonWidth = width * 0.15;
rectangle('Position', [x + width/2 - ribbonWidth/2, y, ribbonWidth, height], ...
'FaceColor', ribbonColor, 'EdgeColor', 'none');
% Horizontal ribbon
ribbonHeight = height * 0.15;
rectangle('Position', [x, y + height/2 - ribbonHeight/2, width, ribbonHeight], ...
'FaceColor', ribbonColor, 'EdgeColor', 'none');
% Bow on top
bowX = x + width/2;
bowY = y + height;
bowSize = width * 0.2;
% Left loop
theta = linspace(0, pi, 30);
fill(bowX - bowSize*0.3 + bowSize*0.5*cos(theta), ...
bowY + bowSize*0.5*sin(theta), ribbonColor, 'EdgeColor', 'none');
% Right loop
fill(bowX + bowSize*0.3 + bowSize*0.5*cos(theta), ...
bowY + bowSize*0.5*sin(theta), ribbonColor, 'EdgeColor', 'none');
% Center knot
theta = linspace(0, 2*pi, 30);
fill(bowX + bowSize*0.25*cos(theta), bowY + bowSize*0.25*sin(theta), ...
ribbonColor*0.8, 'EdgeColor', 'none');
end
I like this quote, what do you think?
"If the part of programming you enjoy most is the physical act of writing code, then agents will feel beside the point. You’re already where you want to be, even just with some Copilot or Cursor-style intelligent code auto completion, which makes you faster while still leaving you fully in the driver’s seat about the code that gets written.
But if the part you care about is the decision-making around the code, agents feel like they clear space. They take care of the mechanical expression and leave you with judgment, tradeoffs, and intent. Because truly, for someone at my experience level, that is my core value offering anyway. When I spend time actually typing code these days with my own fingers, it feels like a waste of my time."
— Obie Fernandez, What happens when the coding becomes the least interesting part of the work
I can't believe someone put time into this ;-)

In a recent blog post, @Guy Rouleau writes about the new Simulink Copilot Beta. Sign ups are on the Copilot Beta page below. Let him know what you think.
Guy's Blog Post - https://blogs.mathworks.com/simulink/2025/12/01/a-copilot-for-simulink/
Simulink Copilot Beta - https://www.mathworks.com/products/simulink-copilot.html

The formula comes from @yuruyurau. (https://x.com/yuruyurau)
digital life 1

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:2e4;
x = mod(i, 100);
y = floor(i./100);
k = x./4 - 12.5;
e = y./9 + 5;
o = vecnorm([k; e])./9;
while true
t = t + pi/90;
q = x + 99 + tan(1./k) + o.*k.*(cos(e.*9)./4 + cos(y./2)).*sin(o.*4 - t);
c = o.*e./30 - t./8;
SHdl.XData = (q.*0.7.*sin(c)) + 9.*cos(y./19 + t) + 200;
SHdl.YData = 200 + (q./2.*cos(c));
drawnow
end
digital life 2

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = i;
y = i./235;
e = y./8 - 13;
while true
t = t + pi/240;
k = (4 + sin(y.*2 - t).*3).*cos(x./29);
d = vecnorm([k; e]);
q = 3.*sin(k.*2) + 0.3./k + sin(y./25).*k.*(9 + 4.*sin(e.*9 - d.*3 + t.*2));
SHdl.XData = q + 30.*cos(d - t) + 200;
SHdl.YData = 620 - q.*sin(d - t) - d.*39;
drawnow
end
digital life 3

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = mod(i, 200);
y = i./43;
k = 5.*cos(x./14).*cos(y./30);
e = y./8 - 13;
d = (k.^2 + e.^2)./59 + 4;
a = atan2(k, e);
while true
t = t + pi/20;
q = 60 - 3.*sin(a.*e) + k.*(3 + 4./d.*sin(d.^2 - t.*2));
c = d./2 + e./99 - t./18;
SHdl.XData = q.*sin(c) + 200;
SHdl.YData = (q + d.*9).*cos(c) + 200;
drawnow; pause(1e-2)
end
digital life 4

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:4e4;
x = mod(i, 200);
y = i./200;
k = x./8 - 12.5;
e = y./8 - 12.5;
o = (k.^2 + e.^2)./169;
d = .5 + 5.*cos(o);
while true
t = t + pi/120;
SHdl.XData = x + d.*k.*sin(d.*2 + o + t) + e.*cos(e + t) + 100;
SHdl.YData = y./4 - o.*135 + d.*6.*cos(d.*3 + o.*9 + t) + 275;
SHdl.CData = ((d.*sin(k).*sin(t.*4 + e)).^2).'.*[1,1,1];
drawnow;
end
digital life 5

figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 1, 'filled','o','w',...
'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 0:1e4;
x = mod(i, 200);
y = i./55;
k = 9.*cos(x./8);
e = y./8 - 12.5;
while true
t = t + pi/120;
d = (k.^2 + e.^2)./99 + sin(t)./6 + .5;
q = 99 - e.*sin(atan2(k, e).*7)./d + k.*(3 + cos(d.^2 - t).*2);
c = d./2 + e./69 - t./16;
SHdl.XData = q.*sin(c) + 200;
SHdl.YData = (q + 19.*d).*cos(c) + 200;
drawnow;
end
digital life 6

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 1:1e4;
y = i./790;
k = y; idx = y < 5;
k(idx) = 6 + sin(bitxor(floor(y(idx)), 1)).*6;
k(~idx) = 4 + cos(y(~idx));
while true
t = t + pi/90;
d = sqrt((k.*cos(i + t./4)).^2 + (y/3-13).^2);
q = y.*k.*cos(i + t./4)./5.*(2 + sin(d.*2 + y - t.*4));
c = d./3 - t./2 + mod(i, 2);
SHdl.XData = q + 90.*cos(c) + 200;
SHdl.YData = 400 - (q.*sin(c) + d.*29 - 170);
drawnow; pause(1e-2)
end
digital life 7

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.4);
t = 0;
i = 1:1e4;
y = i./345;
x = y; idx = y < 11;
x(idx) = 6 + sin(bitxor(floor(x(idx)), 8))*6;
x(~idx) = x(~idx)./5 + cos(x(~idx)./2);
e = y./7 - 13;
while true
t = t + pi/120;
k = x.*cos(i - t./4);
d = sqrt(k.^2 + e.^2) + sin(e./4 + t)./2;
q = y.*k./d.*(3 + sin(d.*2 + y./2 - t.*4));
c = d./2 + 1 - t./2;
SHdl.XData = q + 60.*cos(c) + 200;
SHdl.YData = 400 - (q.*sin(c) + d.*29 - 170);
drawnow; pause(5e-3)
end
digital life 8

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl{6} = [];
for j = 1:6
SHdl{j} = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.3);
end
t = 0;
i = 1:2e4;
k = mod(i, 25) - 12;
e = i./800; m = 200;
theta = pi/3;
R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
while true
t = t + pi/240;
d = 7.*cos(sqrt(k.^2 + e.^2)./3 + t./2);
XY = [k.*4 + d.*k.*sin(d + e./9 + t);
e.*2 - d.*9 - d.*9.*cos(d + t)];
for j = 1:6
XY = R*XY;
SHdl{j}.XData = XY(1,:) + m;
SHdl{j}.YData = XY(2,:) + m;
end
drawnow;
end
digital life 9

clc; clear
figure('Position',[300,50,900,900], 'Color','k');
axes(gcf, 'NextPlot','add', 'Position',[0,0,1,1], 'Color','k');
axis([0, 400, 0, 400])
SHdl{14} = [];
for j = 1:14
SHdl{j} = scatter([], [], 2, 'filled','o','w', 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.1);
end
t = 0;
i = 1:2e4;
k = mod(i, 50) - 25;
e = i./1100; m = 200;
theta = pi/7;
R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
while true
t = t + pi/240;
d = 5.*cos(sqrt(k.^2 + e.^2) - t + mod(i, 2));
XY = [k + k.*d./6.*sin(d + e./3 + t);
90 + e.*d - e./d.*2.*cos(d + t)];
for j = 1:14
XY = R*XY;
SHdl{j}.XData = XY(1,:) + m;
SHdl{j}.YData = XY(2,:) + m;
end
drawnow;
end
The challenge:
You are given a string of lowercase letters 'a' to 'z'.
Each character represents a base-26 digit:
- 'a' = 0
1. Understand the Base-26 Conversion Process:
Let the input be s = 'aloha'.
Convert each character to a digit:
digits = double(s) - double('a');
This works because:
double('a') = 97
double('b') = 98
So:
double('a') - 97 = 0
double('l') - 97 = 11
double('o') - 97 = 14
double('h') - 97 = 7
double('a') - 97 = 0
Now you have:
[0 11 14 7 0]
2. Interpret as Base-26:
For a number with n digits:
d1 d2 d3 ... dn
Value = d1*26^(n-1) + d2*26^(n-2) + ... + dn*26^0
So for 'aloha' (5 chars):
0*26^4 + 11*26^3 + 14*26^2 + 7*26^1 + 0*26^0
MATLAB can compute this automatically.
3. Avoid loops — Use MATLAB vectorization:
You can compute the weighted sum using dot
digits = double(s) - 'a';
powers = 26.^(length(s)-1:-1:0);
result = dot(digits, powers);
This is clean, short, and vectorized.
4.Test with the examples:
char2num26('funfunfun')
→ 1208856210289
char2num26('matlab')
→ 142917893
char2num26('nasa')
→ 228956

% Recreation of Saturn photo
figure('Color', 'k', 'Position', [100, 100, 800, 800]);
ax = axes('Color', 'k', 'XColor', 'none', 'YColor', 'none', 'ZColor', 'none');
hold on;
% Create the planet sphere
[x, y, z] = sphere(150);
% Saturn colors - pale yellow/cream gradient
saturn_radius = 1;
% Create color data based on latitude for gradient effect
lat = asin(z);
color_data = rescale(lat, 0.3, 0.9);
% Plot Saturn with smooth shading
planet = surf(x*saturn_radius, y*saturn_radius, z*saturn_radius, ...
color_data, ...
'EdgeColor', 'none', ...
'FaceColor', 'interp', ...
'FaceLighting', 'gouraud', ...
'AmbientStrength', 0.3, ...
'DiffuseStrength', 0.6, ...
'SpecularStrength', 0.1);
% Use a cream/pale yellow colormap for Saturn
cream_map = [linspace(0.4, 0.95, 256)', ...
linspace(0.35, 0.9, 256)', ...
linspace(0.2, 0.7, 256)'];
colormap(cream_map);
% Create the ring system
n_points = 300;
theta = linspace(0, 2*pi, n_points);
% Define ring structure (inner radius, outer radius, brightness)
rings = [
1.2, 1.4, 0.7; % Inner ring
1.45, 1.65, 0.8; % A ring
1.7, 1.85, 0.5; % Cassini division (darker)
1.9, 2.3, 0.9; % B ring (brightest)
2.35, 2.5, 0.6; % C ring
2.55, 2.8, 0.4; % Outer rings (fainter)
];
% Create rings as patches
for i = 1:size(rings, 1)
r_inner = rings(i, 1);
r_outer = rings(i, 2);
brightness = rings(i, 3);
% Create ring coordinates
x_inner = r_inner * cos(theta);
y_inner = r_inner * sin(theta);
x_outer = r_outer * cos(theta);
y_outer = r_outer * sin(theta);
% Front side of rings
ring_x = [x_inner, fliplr(x_outer)];
ring_y = [y_inner, fliplr(y_outer)];
ring_z = zeros(size(ring_x));
% Color based on brightness
ring_color = brightness * [0.9, 0.85, 0.7];
fill3(ring_x, ring_y, ring_z, ring_color, ...
'EdgeColor', 'none', ...
'FaceAlpha', 0.7, ...
'FaceLighting', 'gouraud', ...
'AmbientStrength', 0.5);
end
% Add some texture/gaps in the rings using scatter
n_particles = 3000;
r_particles = 1.2 + rand(1, n_particles) * 1.6;
theta_particles = rand(1, n_particles) * 2 * pi;
x_particles = r_particles .* cos(theta_particles);
y_particles = r_particles .* sin(theta_particles);
z_particles = (rand(1, n_particles) - 0.5) * 0.02;
% Vary particle brightness
particle_colors = repmat([0.8, 0.75, 0.6], n_particles, 1) .* ...
(0.5 + 0.5*rand(n_particles, 1));
scatter3(x_particles, y_particles, z_particles, 1, particle_colors, ...
'filled', 'MarkerFaceAlpha', 0.3);
% Add dramatic outer halo effect - multiple layers extending far out
n_glow = 20;
for i = 1:n_glow
glow_radius = 1 + i*0.35; % Extend much farther
alpha_val = 0.08 / sqrt(i); % More visible, slower falloff
% Color gradient from cream to blue/purple at outer edges
if i <= 8
glow_color = [0.9, 0.85, 0.7]; % Warm cream/yellow
else
% Gradually shift to cooler colors
mix = (i - 8) / (n_glow - 8);
glow_color = (1-mix)*[0.9, 0.85, 0.7] + mix*[0.6, 0.65, 0.85];
end
surf(x*glow_radius, y*glow_radius, z*glow_radius, ...
ones(size(x)), ...
'EdgeColor', 'none', ...
'FaceColor', glow_color, ...
'FaceAlpha', alpha_val, ...
'FaceLighting', 'none');
end
% Add extensive glow to rings - make it much more dramatic
n_ring_glow = 12;
for i = 1:n_ring_glow
glow_scale = 1 + i*0.15; % Extend farther
alpha_ring = 0.12 / sqrt(i); % More visible
for j = 1:size(rings, 1)
r_inner = rings(j, 1) * glow_scale;
r_outer = rings(j, 2) * glow_scale;
brightness = rings(j, 3) * 0.5 / sqrt(i);
x_inner = r_inner * cos(theta);
y_inner = r_inner * sin(theta);
x_outer = r_outer * cos(theta);
y_outer = r_outer * sin(theta);
ring_x = [x_inner, fliplr(x_outer)];
ring_y = [y_inner, fliplr(y_outer)];
ring_z = zeros(size(ring_x));
% Color gradient for ring glow
if i <= 6
ring_color = brightness * [0.9, 0.85, 0.7];
else
mix = (i - 6) / (n_ring_glow - 6);
ring_color = brightness * ((1-mix)*[0.9, 0.85, 0.7] + mix*[0.65, 0.7, 0.9]);
end
fill3(ring_x, ring_y, ring_z, ring_color, ...
'EdgeColor', 'none', ...
'FaceAlpha', alpha_ring, ...
'FaceLighting', 'none');
end
end
% Add diffuse glow particles for atmospheric effect
n_glow_particles = 8000;
glow_radius_particles = 1.5 + rand(1, n_glow_particles) * 5;
theta_glow = rand(1, n_glow_particles) * 2 * pi;
phi_glow = acos(2*rand(1, n_glow_particles) - 1);
x_glow = glow_radius_particles .* sin(phi_glow) .* cos(theta_glow);
y_glow = glow_radius_particles .* sin(phi_glow) .* sin(theta_glow);
z_glow = glow_radius_particles .* cos(phi_glow);
% Color particles based on distance - cooler colors farther out
particle_glow_colors = zeros(n_glow_particles, 3);
for i = 1:n_glow_particles
dist = glow_radius_particles(i);
if dist < 3
particle_glow_colors(i,:) = [0.9, 0.85, 0.7];
else
mix = (dist - 3) / 4;
particle_glow_colors(i,:) = (1-mix)*[0.9, 0.85, 0.7] + mix*[0.5, 0.6, 0.9];
end
end
scatter3(x_glow, y_glow, z_glow, rand(1, n_glow_particles)*2+0.5, ...
particle_glow_colors, 'filled', 'MarkerFaceAlpha', 0.05);
% Lighting setup
light('Position', [-3, -2, 4], 'Style', 'infinite', ...
'Color', [1, 1, 0.95]);
light('Position', [2, 3, 2], 'Style', 'infinite', ...
'Color', [0.3, 0.3, 0.4]);
% Camera and view settings
axis equal off;
view([-35, 25]); % Angle to match saturn_photo.jpg - more dramatic tilt
camva(10); % Field of view - slightly wider to show full halo
xlim([-8, 8]); % Expanded to show outer halo
ylim([-8, 8]);
zlim([-8, 8]);
% Material properties
material dull;
title('Saturn - Left click: Rotate | Right click: Pan | Scroll: Zoom', 'Color', 'w', 'FontSize', 12);
% Enable interactive camera controls
cameratoolbar('Show');
cameratoolbar('SetMode', 'orbit'); % Start in rotation mode
% Custom mouse controls
set(gcf, 'WindowButtonDownFcn', @mouseDown);
function mouseDown(src, ~)
selType = get(src, 'SelectionType');
switch selType
case 'normal' % Left click - rotate
cameratoolbar('SetMode', 'orbit');
rotate3d on;
case 'alt' % Right click - pan
cameratoolbar('SetMode', 'pan');
pan on;
end
end
To track the current leader after each match, you can use cumulative scores. First, calculate the cumulative sum for each player across the matches. Then, after eaayer with the highest score.
Hint: Use cumsum(S, 1) to get cumulative scores along the rows (matches). Loop through each row to keep track of the leader. If multiple players tie, pick the lowest index.
Example:
If S = [5 3 4; 2 6 2; 3 5 7], after match 3, the cumulative scores are [10 14 13]. Player 2 leads with 14 hilbs.
This method keeps your code clean and avoids repeatedly summing rows.
Congratulations to all the Cool Coders who have completed the problem set. I hope you weren't too cool to enjoy the silliness I put into the problems.
If you've solved the whole problem set, don't forget to help out your teammates with suggestions, tips, tricks, etc. But also, just for fun, I'm curious to see which of my many in-jokes and nerdy references you noticed. Many of the problems were inspired by things in the real world, then ported over into the chaotic fantasy world of Nedland.
I guess I'll start with the obvious real-world reference: @Ned Gulley (I make no comment about his role as insane despot in any universe, real or otherwise.)
Extracting the digits of a number will be useful to solve many Cody problems.
Instead of iteratively dividing by 10 and taking the remainder, the digits of a number can be easily extracted using String operations.
%Extract the digits of N
N = 1234;
d = num2str(N)-'0';
d =
1 2 3 4
Instead of looping with if-statements, use logical indexing:
A(A < 0) = 0;
One line, no loops, full clarity.
Whenever a problem repeats in cycles (like indexing or angles), mod() keeps your logic clean:
idx = mod(i-1, n) + 1;
No if-else chaos!
The toughest problem in the Cody Contest 2025 is Clueless - Lord Ned in the Game Room. Thank you Matt Tearle for such as wonderful problem. We can approach this clueless(!) tough problem systematically.
Initialize knowledge Matrix
Based on the hints provided in the problem description, we can initialize a knowledge matrix of size n*3 by m+1. The rows of the knowledge matrix represent the different cards and the columns represent the players. In the knowledge matrix, the first n rows represent category 1 cards, the next n rows, category 2 and the next category 3. We can initialize this matrix with zeros. On the go, once we know that a player holds the card, we can make that entry as 1 and if a player doesn't have the card, we can make that entry as -1.
yourcards processing
These are cards received by us.
- In the knowledge matrix, mark the entries as 1 for the cards received. These entries will be the some elements along the column pnum of the knowledge matrix.
- Mark all other entries along the column pnum as -1, as we don't receive other cards.
- Mark all other entries along the rows corresponding to the received cards as -1, as other players cannot receive the cards that are with us.
commoncards processing
These are the common cards kept open.
- In the knowledge matrix, mark the entries as 1 for the common cards. These entries will be some elements along the column (m+1) of the knowledge matrix.
- Mark all other entries along the column (m+1) as -1, as other cards are not common.
- Mark all other entries along the rows corresponding to the common cards as -1, as other players cannot receive the cards that are common.
Result -1 processing
In the turns input matrix, the result (5th column) value -1 means, the corresponding player doesn't have the 3 cards asked.
- Find all the rows with result as -1.
- For those corresponding players (1st element in each row of turns matrix), mark -1 entries in the knowledge matrix for those 3 absent cards.
pnum turns processing
These are our turns, so we get definite answers for the asked cards. Make sure to traverse only the rows corresponding to our turn.
- The results with -1 are already processed in the previous step.
- The results other than -1 means, that particular card is present with the asked player. So mark the entry as 1 for the corresponding player in the knowledge matrix.
- Mark all other entries along the row corresponding to step 2 as -1, as other players cannot receive this card.
Result 0 processing
So far, in the yourcards processing, commoncards processing, result -1 processing and pnum turns processing, we had very straightforward definite knowledge about the presence/absence of the card with a player. This step onwards, the tricky part of the problem begins.
result 0 means, any one (or more) of the asked cards are present with the asked player. We don't know exactly which card.
- For the asked player, if we have a definite no answer (-1 value in the knowledge matrix) for any two of the three asked cards, then we are sure about the card that is present with the player.
- Mark the entry as 1 for the definitely known card for the corresponding player in the knowledge matrix.
- Mark all other entries along the row corresponding to step 2 as -1, as other players cannot receive this card.
Cards per Player processing
Based on the number of cards present in the yourcards, we know the ncards, the number of cards per player.
Check along each column of the knowledge matrix, that is for each player.
- If the number of ones (definitely present cards) is equal to ncards, we can make all other entries along the column as -1, as this player cannot have any other card.
- If the sum of number of ones (definitely present cards) and the number of zeros (unknown cards) is equal to ncards, we can (i) mark the zero entries as one, as the unknown cards have become definitely present cards, (ii) mark all other entries along the column as -1, as other players cannot have any other card.
Category-wise cards checking
For each category, we must get a definite card to be present in the envelope.
- In each category (For every group of n rows of knowledge matrix), check for a row with all -1s. That is a card which is definitely not present with any of the players. Then this card will surely be present in the envelope. Add it to the output.
- If we could not find an all -1 row, then in that category, check each row for a 1 to be present. Note down the rows which doesn't have a 1. Those cards' players are still unknown. If we have only one such row (unknown card), then it must be in the envelope, as from each category one card is present in the envelope. Add it to the output.
- For the card identified in Step 2, mark all the entries along that row in the knowledge matrix as -1, as this card doesn't belong to any player.
Looping Over
In our so far steps, we could note that, the knowledge matrix got updated even after "Result 0 processing" step. This updation in the knowledge matrix may help the "Result 0 processing" step, if we perform it again. So, we can loop over the steps, "Result 0 processing", "Cards per Player processing" and "Category-wise cards checking" again. This ensures that, we will get the desired number of envelop cards (three in our case) as output.
Experimenting with Agentic AI
44%
I am an AI skeptic
0%
AI is banned at work
11%
I am happy with Conversational AI
44%
9 votes
Instead of growing arrays inside a loop, preallocate with zeros(), ones(), or nan(). It avoids memory fragmentation and speeds up Cody solutions.
A = zeros(1,1000);
Cody often hides subtle hints in example outputs — like data shape, rounding, or format. Matching those exactly saves you a lot of debugging time.
Pure Matlab
82%
Simulink
18%
11 votes

