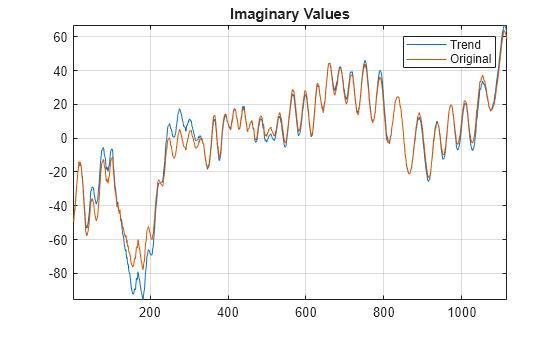icwt
Inverse continuous 1-D wavelet transform
Syntax
Description
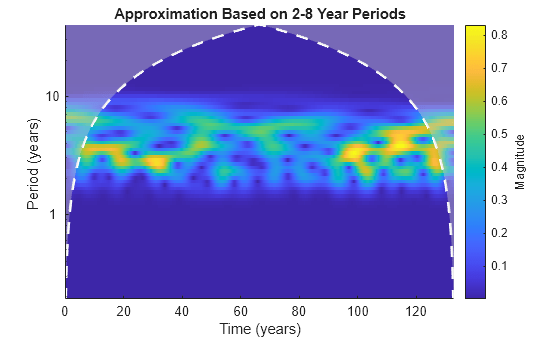
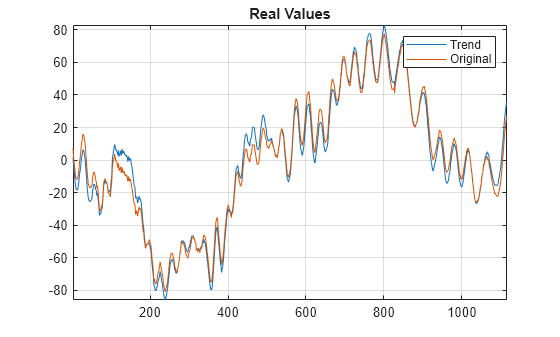
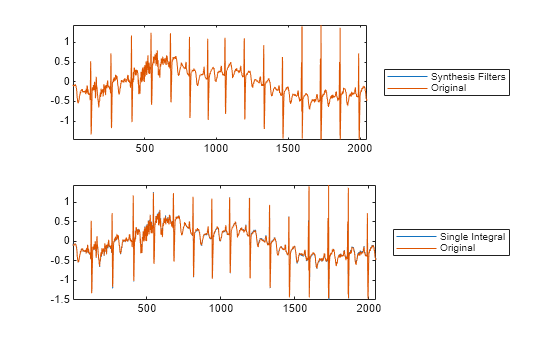
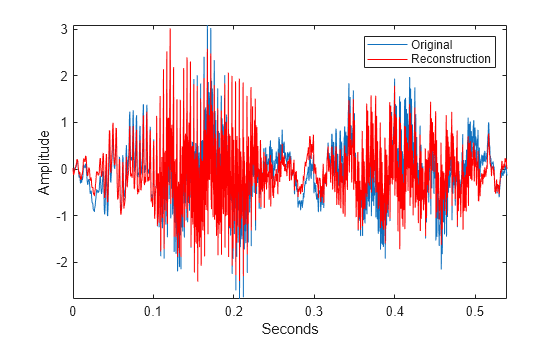
xrec = icwt(cfs)cfs using Morlet's single integral formula.
icwt assumes that you obtained the CWT using cwt with the default analytic Morse
(3,60) wavelet. This wavelet has a symmetry of 3 and a time bandwidth of 60.
icwt also assumes that the CWT uses default scales.
xrec = icwt(___,f,freqrange)freqrange. f is the scale-to-frequency
conversion obtained from cwt.
In R2022a: If you invert the CWT over a specified frequency range, you
must precede those inputs either by a wavelet name or an empty input for the default
Morse wavelet. For more information, see icwt behavior change.
xrec = icwt(___,period,periodrange)periodrange. p is an array of
durations obtained from cwt with a duration input. The
period is the cwt output obtained using a
duration input. The period range
must be increasing and contained in period.
In R2022a: If you invert the CWT over a specified range of periods, you
must precede those inputs either by a wavelet name or an empty input for the default
Morse wavelet. For more information, see icwt behavior change.
xrec = icwt(___,Name=Value)xrec =
icwt(cfs,TimeBandwidth=40,VoicesPerOctave=20) specifies a
time-bandwidth product of 40 and 20 voices per octave.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Lilly, J. M., and S. C. Olhede. "Generalized Morse Wavelets as a Superfamily of Analytic Wavelets." IEEE Transactions on Signal Processing 60, no. 11 (November 2012): 6036–41. https://doi.org/10.1109/TSP.2012.2210890.
[2] Lilly, J.M., and S.C. Olhede. "Higher-Order Properties of Analytic Wavelets." IEEE Transactions on Signal Processing 57, no. 1 (January 2009): 146–60. https://doi.org/10.1109/TSP.2008.2007607.
[3] Lilly, J. M. jLab: A data analysis package for MATLAB®, version 1.6.2. 2016. http://www.jmlilly.net/jmlsoft.html.
[4] Lilly, J. M., and J.-C. Gascard. "Wavelet Ridge Diagnosis of Time-Varying Elliptical Signals with Application to an Oceanic Eddy." Nonlinear Processes in Geophysics 13, no. 5 (September 14, 2006): 467–83. https://doi.org/10.5194/npg-13-467-2006.
[5] Duval-Destin, M., M. A. Muschietti, and B. Torresani. “Continuous Wavelet Decompositions, Multiresolution, and Contrast Analysis.” SIAM Journal on Mathematical Analysis 24, no. 3 (May 1993): 739–55. https://doi.org/10.1137/0524045.
[6] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[7] Torrence, Christopher, and Gilbert P. Compo. “A Practical Guide to Wavelet Analysis.” Bulletin of the American Meteorological Society 79, no. 1 (January 1, 1998): 61–78. https://doi.org/10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2.
[8] Holschneider, M., and Ph. Tchamitchian. “Pointwise Analysis of Riemann’s 'Nondifferentiable' Function.” Inventiones Mathematicae 105, no. 1 (December 1991): 157–75. https://doi.org/10.1007/BF01232261.
![Figure contains 2 axes objects. Axes object 1 with title Original Data, ylabel Amplitude contains an object of type line. Axes object 2 with title Bandpass Filtered Reconstruction [0.030 0.070] Hz, xlabel Time (s), ylabel Amplitude contains an object of type line.](../../examples/wavelet/win64/ReconstructFrequencyLocalizedEarthquakeDataExample_01.png)