wsst
Wavelet synchrosqueezed transform
Syntax
Description
sst = wsst(x)x. The wsst
function computes the synchrosqueezed transform using the analytic Morlet wavelet.
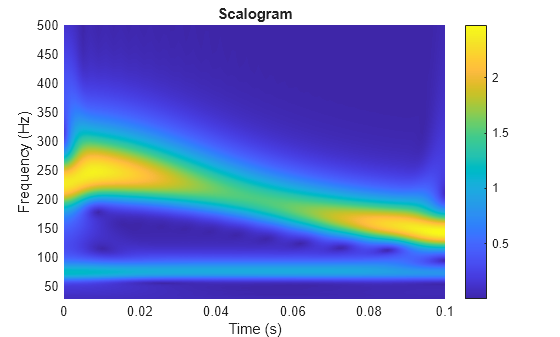
The synchrosqueezed transform has reduced energy smearing when compared to the
continuous wavelet transform (CWT). The wsst function normalizes the
analyzing wavelets to preserve the L1 norm. For more information, see Algorithms.
[___] = wsst(___, uses
the analytic wavelet specified by wav)wav to compute the synchrosqueezed
transform.
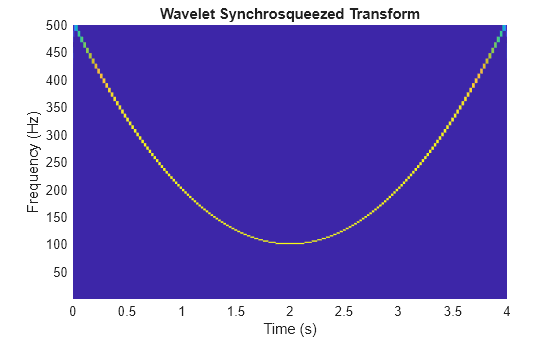
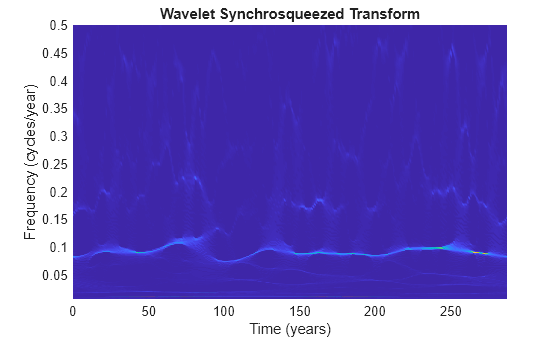
wsst(___) with no output arguments plots the magnitude of the
synchrosqueezed transform as a function of time and frequency. If you do not specify a
sampling frequency or interval, the synchrosqueezed transform is plotted in cycles per
sample. If you specify a sampling frequency, the synchrosqueezed transform is plotted in
hertz. If you specify a sampling interval using a duration, the plot is in cycles per unit
time. The time units are derived from the duration.
[___] = wsst(___,
returns the synchrosqueezed transform with additional options specified by one or more
name-value arguments.Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The wsst function normalizes the analyzing wavelets to preserve the
L1 norm. An equivalent way to state this is that wsst does not multiply
the Fourier transforms of the wavelet bandpass filters by the square root of the scale.
Multiplying by the square root of the scale would unequally weight different bandpass
contributions.
With L1 normalization, if you have equal amplitude oscillatory components in your data at
different scales, they will have equal magnitude in the CWT. The cwt function also uses L1 normalization. For more information, see L1 Norm for CWT.
References
[1] Daubechies, Ingrid, Jianfeng Lu, and Hau-Tieng Wu. “Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-like Tool.” Applied and Computational Harmonic Analysis 30, no. 2 (March 2011): 243–61. https://doi.org/10.1016/j.acha.2010.08.002.
[2] Thakur, Gaurav, Eugene Brevdo, Neven S. Fučkar, and Hau-Tieng Wu. “The Synchrosqueezing Algorithm for Time-Varying Spectral Analysis: Robustness Properties and New Paleoclimate Applications.” Signal Processing 93, no. 5 (May 2013): 1079–94. https://doi.org/10.1016/j.sigpro.2012.11.029.