Pearson Distribution
The Pearson distribution is a four-parameter distribution that has an arbitrary mean, standard deviation, skewness, and kurtosis. This distribution is often used to model asymmetric data that is prone to outliers.
Statistics and Machine Learning Toolbox™ offers several ways to work with the Pearson distribution:
Create a probability distribution object
PearsonDistributionby specifying parameter values usingmakedist. Then, use object functions to evaluate the distribution, generate random numbers, and so on.Use distribution-specific functions (
pearspdf,pearscdf,pearsrnd,pearsinv) with specified distribution parameters. The distribution-specific functions can accept parameters of multiple Pearson distributions.Use generic distribution functions (
cdf,pdf,random,icdf) by specifying the distribution name"Pearson"with specified distribution parameters or by using the distribution objectPearsonDistribution.
Types
The Pearson distribution has eight types, most of which correspond to other known distributions.
| Pearson Distribution Type | Description |
|---|---|
0 | Normal |
1 | 4-parameter beta |
2 | Symmetric 4-parameter beta |
3 | 3-parameter gamma |
4 | Distribution specific to the Pearson system with pdf proportional to , where a and b are quantities related to the differential equation that defines the Pearson distribution |
5 | Inverse 3-parameter gamma |
6 | F location scale |
7 | Student's t location scale |
Parameters
The Pearson distribution uses the following parameters:
| Parameter | Description |
|---|---|
| μ | Mean |
| σ | Standard deviation |
| γ | Skewness. γ is a measure of the asymmetry of the data around the sample mean. If the skewness is negative, the data spreads out more to the left of the mean than to the right. If the skewness is positive, the data spreads out more to the right. γ2 must be less than κ – 1. |
| κ | Kurtosis. κ is a measure of how prone a distribution is to outliers. The kurtosis of the normal distribution is 3. Distributions that are more prone to outliers than the normal distribution have a kurtosis value greater than 3; distributions that are less prone have a kurtosis value less than 3. κ must be greater than γ2 + 1. |
Probability Density Function
The Pearson distribution probability density function (pdf) is the solution to the differential equation
where the system is defined by the coefficients for 0 ≤ j ≤ 2. For most distribution types, the pdf is a closed-form function. The following table describes the pdf for each distribution type.
| Pearson Distribution Type | pdf p(x) |
|---|---|
0 |
|
1 | , where B is the Beta Function, lb and ub are the lower and upper bounds of the distribution (respectively), a > 0 is a shape parameter, and b > 0 is a scale parameter |
2 | |
3 | , where Γ is the Gamma Function |
4 | , where m > 0 and ν > 0 are shape parameters |
5 | |
6 | , where ν1 > 0 and ν2 > 0 are shape parameters |
7 |
Cumulative Distribution Function
The Pearson distribution cumulative distribution function (cdf) is the integral of the pdf. The following table describes the cdf for each distribution type.
| Pearson Distribution Type | cdf c(x) |
|---|---|
0 | |
1 | , where B is the Beta Function, lb and ub are the lower and upper bounds of the distribution (respectively), a > 0 is a shape parameter, and b > 0 is a scale parameter |
2 |
|
3 | |
4 | A type 4 Pearson distribution does not have a closed-form
cdf. You can evaluate the type 4 Pearson distribution cdf at a
point x by numerically integrating the pdf
from –∞ to x. Use pearscdf or cdf to evaluate the
cdf. |
5 | , where Q is the Incomplete Gamma Function |
6 | , where I is the regularized incomplete beta function, and ν1 > 0 and ν2 > 0 are shape parameters |
7 | , where ν > 0 is a shape parameter |
Support
For some Pearson distribution types, support for the pdf and cdf is given by the
coefficients in the differential equation that defines the pdf. The following
table shows the support for the Pearson distribution pdf and cdf when μ = 0 and σ = 1. The variables a1 and a2 are
solutions to the equation , and a1 < a2.
| Pearson Distribution Type | Support |
|---|---|
0 | (-Inf,Inf) |
1 | (a1,a2) |
2 | (-a1,a1) |
3 | (a1,Inf) when a>0 and
(-Inf,a1) when
a<0 |
4 | (-Inf,Inf) |
5 | (-C1,Inf) when (b1-C1)/b2
<0, and (-Inf,C1) otherwise.
C1 = b1/(2*b2). |
6 | (a2,Inf) when a1 and
a2 are negative, and
(-Inf,a1) when a1 and
a2 are positive |
7 | (-Inf,Inf) |
For distributions with μ ≠ 0 or σ ≠ 1, the bounds of the support are shifted from the bounds given in the preceding table. In this case, you can calculate the lower and upper bounds lb and ub as follows:
lb = σlb*+μ
ub = σub*+μ
where lb* and ub* are the lower and upper bounds given in the preceding table for the same distribution type.
Examples
Compare Pearson Distributions
Create the variables mu0, sigma0, skew0, and kurt0, which contain the parameters for a Pearson distribution of type 0.
mu0 = 0; sigma0 = 1; skew0 = 0; kurt0 = 3;
Use the pearspdf and pearscdf functions to evaluate the pdf and cdf, respectively, for the type 0 Pearson distribution between –5 and 5. You can create a vector of points between –5 and 5 by using the linspace function. Confirm that mu0, sigma0, skew0, and kurt0 define a Pearson distribution of type 0.
x0 = linspace(-5,5,100); [p0,type0] = pearspdf(x0,mu0,sigma0,skew0,kurt0); c0 = pearscdf(x0,mu0,sigma0,skew0,kurt0); type0
type0 = 0
The output shows that p0 contains the pdf for a Pearson distribution of type 0, which is the standard normal distribution.
Draw a random sample of points from the distribution by using the pearsrnd function.
rng(0,"twister") % For reproducibility r0 = pearsrnd(mu0,sigma0,skew0,kurt0,[100,1]);
Repeat the process for a Pearson distribution of type 4. Define the variables mu4, sigma4, skew4, and kurt4. Evaluate the pdf and cdf between –5 and 15, and draw a random sample from the distribution.
mu4 = 5; sigma4 = 1; skew4 = 1; kurt4 = 10; x4 = linspace(-5,15,100); [p4,type4] = pearspdf(x4,mu4,sigma4,skew4,kurt4); c4 = pearscdf(x4,mu4,sigma4,skew4,kurt4); r4 = pearsrnd(mu4,sigma4,skew4,kurt4,[100,1]);
Confirm that mu4, sigma4, skew4, and kurt4 define a Pearson distribution of type 4.
type4
type4 = 4
Repeat the process for a Pearson distribution of type 6, evaluating the pdf and cdf between –10 and 10.
mu6 = 0; sigma6 = 5; skew6 = 3; kurt6 = 20; x6 = linspace(-10,10,100); [p6,type6] = pearspdf(x6,mu6,sigma6,skew6,kurt6); c6 = pearscdf(x6,mu6,sigma6,skew6,kurt6); r6 = pearsrnd(mu6,sigma6,skew6,kurt6,[100,1]);
Confirm that mu6, sigma6, skew6, and kurt6 define a Pearson distribution of type 6.
type6
type6 = 6
Use the tiledlayout and nexttile functions to display box plots of the random samples, pdfs, and cdfs for the Pearson distributions of type 0, 4 and 6. Create box plots of the random samples using the boxchart function.
tiledlayout(3,3) nexttile boxchart(r0) title("Random Sample") ylabel("Type 0",FontWeight="bold") nexttile plot(x0,p0) title("PDF") nexttile plot(x0,c0) title("CDF") nexttile boxchart(r4) ylabel("Type 4",FontWeight="bold") nexttile plot(x4,p4) nexttile plot(x4,c4) nexttile boxchart(r6) ylabel("Type 6",FontWeight="bold") nexttile plot(x6,p6) nexttile plot(x6,c6)
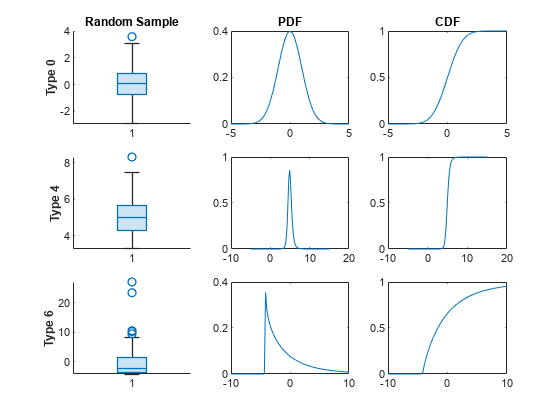
The rows of the figure correspond to the three Pearson distribution types. The first column contains a box plot of the random samples for each distribution. The type 6 Pearson distribution has the largest number of outliers, which is consistent with it having the largest kurtosis of the three distributions. The second column contains a plot of the pdf for each distribution. The pdfs for the type 0 and type 4 Pearson distributions are unbounded, and the type 6 Pearson distribution has a lower bound. The third column shows a plot of the cdf for each distribution. The type 0 and type 4 Pearson distribution cdfs are similarly S-shaped because their pdfs have similar shapes. The type 6 Pearson distribution cdf is concave for values greater than the lower bound.
To calculate the type 6 Pearson distribution lower bound, return the coefficients of the polynomial in the denominator of the ordinary differential equation that defines the Pearson distribution pdf. For more information, see Probability Density Function and Support.
[~,~,coefs6] = pearspdf([],mu6,sigma6,skew6,kurt6)
coefs6 = 1×3
0.7162 0.9324 0.0946
From left to right, the coefficients correspond to terms of increasing order.
Find the roots of the polynomial function by using the roots function. Use the fliplr function to format coefs6 so that, from left to right, the coefficients correspond to terms of decreasing order.
coefs6 = fliplr(coefs6); roots6 = roots(coefs6)
roots6 = 2×1
-9.0175
-0.8396
The roots of the polynomial are negative, indicating that the type 6 Pearson pdf has a lower bound.
To calculate the lower bound, multiply the largest root by sigma6 and add the result to mu6.
lb6 = sigma6*max(roots6) + mu6
lb6 = -4.1982
The lower bound for the support of the type 6 Pearson distribution pdf is near –4, which is consistent with the plot of the pdf.
References
[1] Johnson, Norman Lloyd, et al. "Continuous Univariate Distributions." 2nd ed, vol. 1, Wiley, 1994.
[2] Willink, R. "A Closed-Form Expression for the Pearson Type IV Distribution Function." Australian & New Zealand Journal of Statistics, vol. 50, no. 2, June 2008, pp. 199–205. https://onlinelibrary.wiley.com/doi/10.1111/j.1467-842X.2008.00508.x
See Also
pearspdf | pearscdf | pearsrnd | pearsinv | pdf | cdf | random | icdf | skewness | kurtosis