F Distribution
Definition
The pdf for the F distribution is
where Γ( · ) is the Gamma function.
Background
The F distribution has the following relationship with the chi-square distribution. If χ1 and χ2 are both independent and chi-square distributed with ν1 and ν2 degrees of freedom respectively, then the statistic F below is F-distributed.
The two parameters, ν1 and ν2, are the numerator and denominator degrees of freedom. That is, ν1 and ν2 are the number of independent pieces of information used to calculate χ1 and χ2, respectively.
Examples
Compute the F Distribution pdf
Compute the pdf of an F distribution with 5 numerator degrees of freedom and 3 denominator degrees of freedom.
x = 0:0.01:10; y = fpdf(x,5,3);
Plot the pdf.
figure; plot(x,y)
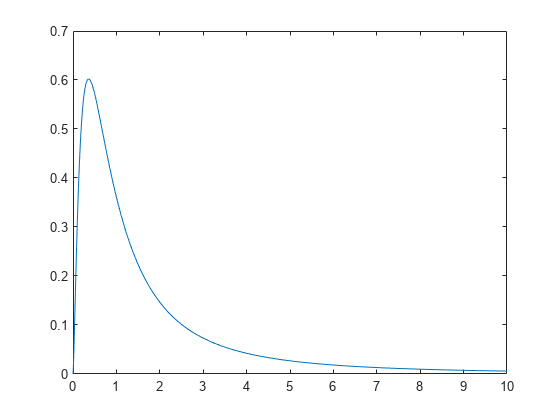
The plot shows that the F distribution exists on positive real numbers and is skewed to the right.
See Also
fcdf | fpdf | finv | fstat | frnd | random