Design PID Control for DC Motor Using Classical Control Theory

Since R2025a

This example shows how to design a PID controller for a DC Motor using classical control theory. Alternatively, you can use Steady State Manager, Model Linearizer, Frequency Response Estimator, or PID tuner apps to streamline the design.

To design the controller using concepts such as gain and phase margin, you need a linearized model. To learn how to linearize models with converters, see Linearize DC-DC Converter Model.

Open Model

Open the DesignDCMotorPIDControl model.

myModel = "DesignDCMotorPIDControl";
open_system(myModel);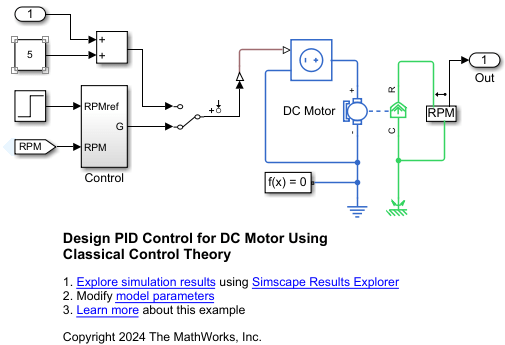

In this example, you model a DC Motor driven by a Controlled Voltage Source block. The Control block provides the control command, which is the voltage applied by the Controlled Voltage Source. You can run the system using closed-loop control or an open-loop.

First, you linearize the model, plot the frequency response, and compute the phase margin. Then you design a proportional control, which changes the magnitude of the Bode plot but does not change the phase. This control reduces oscillations but introduces a larger steady state-error due to the lower gain. You then design a PI control which changes both the gain and phase. This controller eliminates the steady-state error, but the response is slower. Finally, you design a PID control which introduces a response to the derivative of the output, speeding up the response.

Linearize Averaged Switching Model and Plot Frequency Response

Set up the model to allow linearization. Set the model to start from steady state and configure the inputs to run in open loop.

set_param(myModel + "/Solver Configuration",DoDC="on");
set_param(myModel + "/Manual Switch",sw="1");

Linearize the model using the linmod function and obtain a SISO state-space model with the voltage as input and the angular speed as output.

[A,B,C,D] = linmod(myModel);

The transfer function is the Laplace transform of the impulse response of the open-loop system. This equation defines the transfer function in terms of the state-space matrices:

$$G(s)=C(sI-A{)}^{-1}B+D$$

The variable to control is the output speed. Compute the open-loop transfer function G from the state-space representation matrices A, B, C, and D.

G= @(w) C*(1i*w*eye(size(A))-A)^-1*B + D;
figure; plotBodeTransferFunction(G, maxFrequency)

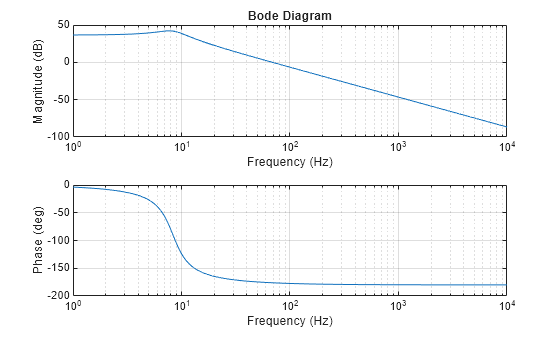
Compute Phase Margin

To calculate the phase margin, first obtain the frequency when the gain is 0 dB and calculate the phase at that frequency. To calculate the gain margin, bring the open-loop system to the verge of instability, which occurs at a phase angle of $$-\pi$$ $$(-180^o)$$.

[gainMargindB,phaseCrossoverPulsation,phaseMargin,gainCrossoverPulsation] = getStabilityCharacteristics(G);

Plot the Bode diagram with stability margins.

figure; plotBodeTransferFunction(G,maxFrequency)
plotPhaseMargin(phaseMargin,gainCrossoverPulsation, maxFrequency);

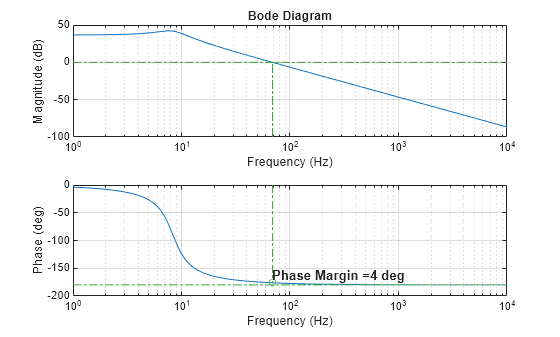
Plot the close-loop step response.

num = [1];
den = [1];
designDCMotorPIDControlPlotRPM("P");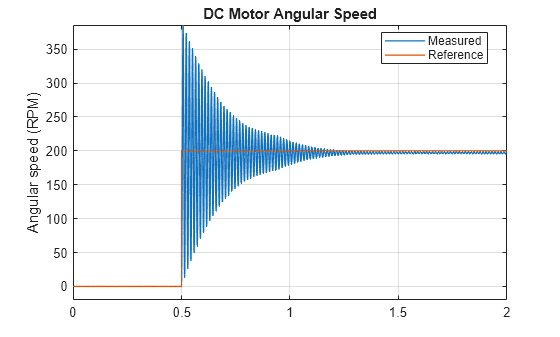

The small phase margin of the open-loop indicates the close-loop system is very close to instability. Consequently, the step response oscillates until the response settles down. Furthermore, there is a small steady-state error that indicates the control needs integral action.

Design Proportional Controller

The plant is already stable. A proportional controller could speed up the response, but also make it unstable.

A proportional controller changes the magnitude of the Bode plot while the phase remains the same.

Choose a crossover frequency with a sufficient phase margin. In this case, 15 Hz allows a phase margin of around $$24^o$$, which is not yet sufficient, but better than the current value.

crossoverFreqP = 15; % Hz
pulsationP = crossoverFreqP*2*pi; % rad/s
phaseMarginP = 180 + angle(G(pulsationP))/pi*180 % deg

phaseMarginP = 
23.7178

Calculate the proportional controller gain.

Kp = 1/abs(G(pulsationP))

Kp = 
0.0362

Plot the new open-loop transfer function with the proportional control.

figure; plotBodeTransferFunction(G, maxFrequency)
Gp = @(w) Kp*(C*(1i*w*eye(size(A))-A)^-1*B + D);
plotBodeTransferFunction(Gp, maxFrequency);

Plot the Bode diagram with the stability margins.

[gainMarginP,phaseCrossoverPulsationP,phaseMarginP,gainCrossoverPulsationP] = getStabilityCharacteristics(Gp);
plotPhaseMargin(phaseMarginP,gainCrossoverPulsationP, maxFrequency);
subplot(2,1,1); legend("Plant","Kp * Plant");

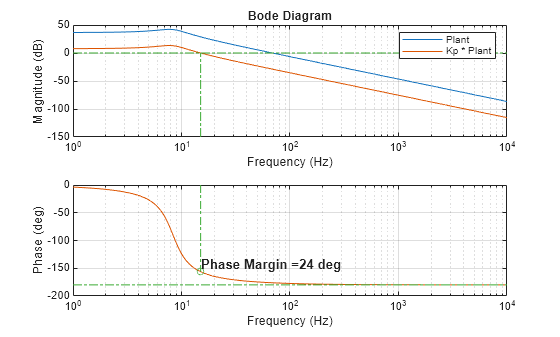
Verify that the close-loop system is now stable by plotting the output voltage of the converter.

num = Kp;
den = 1;
designDCMotorPIDControlPlotRPM("P")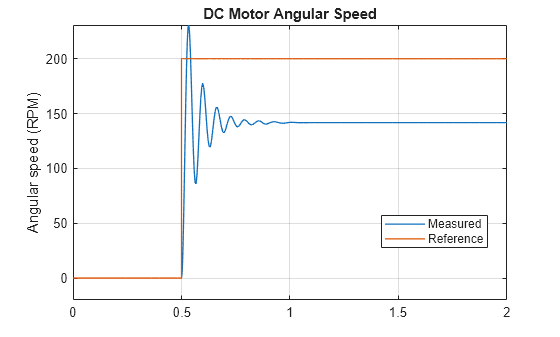

Although the oscilations have been significantly reduced, the plot shows now a bigger a steady-state error due to the lower gain. If you calculate and take a look at the closed-loop transfer function, the order of the numerator and denominator polynomials is the same, which indicates a finite error at steady state for a step input.

Design a Proportional Integral Controller

A proportional-integral controller changes both the gain and the phase of the open-loop Bode plot. The transfer function of the PI control is:

$$C(s)=K_P\frac{1+K_{I}s}{K_{I}s}$$

where:

• $$K_P$$ is the proportional controller gain

• $$K_I$$ is the integral control constant

• $$s$$ is the Fourier transform variable

To calculate the gains analytically, use the following relation of the control gain and phase. From the Bode plot, decide the control gain and phase you need, and then use this expression to calculate the gains.

$$K_P\frac{1+K_I\omega j}{K_I\omega j}=A_C{e}^{j{\varphi }_C}$$

where:

• $$A_C$$ is the amplitude of the control

• $${\varphi }_C$$ is the phase of the control

• $$\omega j$$ is the variable $$s$$ expressed in the time domain

Firstly, decide the value of the crossover frequency and the phase margin. The idea is that a reduction in speed will improve the steady-state accuracy. Reduce around 10-20% the crossover frequency.

crossoverFreqPI = 10; % Hz
phaseMarginPI = 50; % deg
pulsationPI = crossoverFreqPI*2*pi; % rad/s

Then, calculate the amplitude and phase of the plant at this frequency.

gainGpulsationPI = abs(G(pulsationPI));
gainGpulsationPIdB = 20*log10(abs(G(pulsationPI)));
angleGpulsationPI = angle(G(pulsationPI))/pi*180; % deg
controlPhase = -180 + phaseMarginPI - angleGpulsationPI % deg

controlPhase = 
-6.3275

The control will have an angle of $$-6^o$$. Match the phases of both sides of the previous equation to obtain the value of $$K_I$$.

$$\angle \left(\frac{1+K_I\omega j}{K_I\omega j}\right)={\varphi }_C$$; $$\angle (1+K_I\omega j)-\angle (K_I\omega j)={\varphi }_C$$;

If $$\angle (K_I\omega j)=90^{\circ }$$, then $$K_I\omega =\tan (-90^{\circ }+{\varphi }_C)$$

Ki = tand(controlPhase+90)/pulsationPI

Ki = 
0.1435

Calculate the gain of the plant at the gain crossover frequency and obtain the value of the proportional controller gain.

controlPIGain = 1/gainGpulsationPI;
Kp = controlPIGain*pulsationPI*Ki/sqrt(1+(Ki*pulsationPI)^2)

Kp = 
0.0116

Plot the new open-loop transfer function with the PI controller and the step response of the close-loop system.

Gpi = @(w) Kp*(1+Ki*w*1i)/(Ki*w*1i)*(C*(1i*w*eye(size(A))-A)^-1*B + D);
figure; plotBodeTransferFunction(G,maxFrequency);
plotBodeTransferFunction(Gpi, maxFrequency);
[gainMarginPI,phaseCrossoverPulsationPI,phaseMarginPI,gainCrossoverPulsationPI] = getStabilityCharacteristics(Gpi);
plotPhaseMargin(phaseMarginPI,gainCrossoverPulsationPI, maxFrequency);
subplot(2,1,1); legend("Plant","PI * Plant");

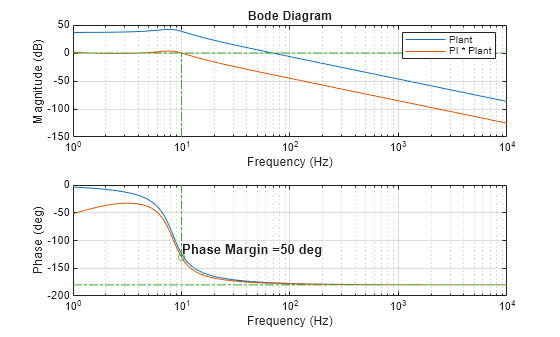
num = [Kp*Ki Kp];
den = [Ki 0];
designDCMotorPIDControlPlotRPM("PI")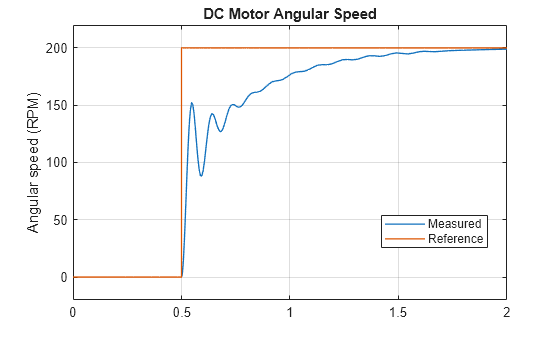

The integral control successfully eliminates the steady-state error. However, the response is now slower. You need derivative action to speed up the response.

Design a Proportional Integral Derivative Controller

A proportional-integral-derivative controller changes both the gain and the phase of the open-loop Bode plot. The control introduces a response to the derivative of the output, which makes the controller faster. The transfer function of the PID control is:

$$C(s)=K_P\frac{1+K_{I}s}{K_{I}s}\frac{1+K_{D}s}{1+N{K}_{D}s}$$

where:

• $$K_P$$ is the proportional controller gain

• $$K_I$$ is the integral control constant

• $$K_D$$ is the derivative control constant

• $$s$$ is the Fourier transform variable

• $$N$$ is the filtering factor

To calculate the gains analytically, use the following relation of the control gain and phase. There are four parameters to determine. Once you have decided the phase margin, you can decide the crossover frequency, the angle of the integral component, and the filtering factor of the derivative component.

$$K_P\frac{1+K_I\omega j}{K_I\omega j}\frac{1+K_D\omega j}{1+N\cdot K_D\omega j}=A_C{e}^{j{\varphi }_C}$$

where:

• $$A_C$$ is the amplitude of the control

• $${\varphi }_C$$ is the phase of the control

• $$\omega j$$ is the variable $$s$$ expressed in the time domain

To start, choose the gain crossover frequency and phase margin. The derivative action compensates for the lag from the integral component, so we can select a frequency greater than the integral and proportional control. Choose a crossover frequency superior to the one of the plant, and the phase margin at least like the integral control.

crossoverFreqPID = 100; % gainCrossoverPulsation; % Hz
phaseMarginPID = 70; % deg

The control gain will be the inverse of the plant at the crossover frequency:

gainGpulsationPID = abs(G(crossoverFreqPID*2*pi));
controlPIDGain = 1/gainGpulsationPID;

Calculate the control phase shift. The Control phase is be the difference between the plant phase and the angle given by the phase margin $$(-180^{\circ }+{\varphi }_M)$$.

pulsationPID = crossoverFreqPID*2*pi; % rad/s
angleGpulsationPID = angle(G(pulsationPID))/pi*180; % deg
controlPhase = -180 + phaseMarginPID - angleGpulsationPID; % deg

Decide the angle of the integral component and calculate the integral control constant $$K_I$$ like you did for the PI control.

integralPhase = -10; %deg
Ki = tand(integralPhase+90)/pulsationPID

Ki = 
0.0090

Having set the phase margin for the PID and the integral action phase, calculate the derivative action phase, $${\varphi }_{PD}$$.

derivativePhase = phaseMarginPID - 180 - angleGpulsationPID - integralPhase %deg

derivativePhase = 
77.3773

Once you have designed the integral action, choose a value of $$N$$. Bear in mind that $$N$$ limits the maximum value of $${\varphi }_{PD}$$, and high values make certain values impossible. If this is the case, reduce the integral phase value to enable higher derivative action phases. Choose a value of 0.01 for $$N$$ and calculate the value $$K_D$$:

N = 0.01;

$${\varphi }_{PD}=atan(K_D\omega )-atan(N{K}_D\omega )$$

Using the trigonometrical identity below, obtain a second order equation, from which you can get two solutions for $$K_D$$:

$$\arctan (a)-\arctan (b)=\arctan \left(\frac{a-b}{1+ab}\right)$$

$$K_D=\frac{(1-N)\pm \sqrt{(N-1{)}^2-4N{\tan }^2{\varphi }_{PD}}}{2\omega N\tan {\varphi }_{PD}}$$

Kd = ((1-N)+sqrt((N-1)^2 - 4*N*(tand(derivativePhase))^2))/(2*pulsationPID*N*tand(derivativePhase))

Kd = 
0.0253

Lastly, calculate the proportional gain using the amplitude equation derived from the control equation:

$$A_C=K_P\left(\frac{\sqrt{I^2+{\omega }^2}}{\omega }\frac{\sqrt{1+K_D^2{\omega }^2}}{\sqrt{1+N^2{K}_D^2{\omega }^2}}\right)$$

Kp = controlPIDGain/(sqrt(Ki^2+pulsationPID^2)/pulsationPID * sqrt(1+Kd^2*pulsationPID^2)/sqrt(1+N^2*Kd^2*pulsationPID^2))

Kp = 
0.1350

Plot the new open-loop transfer function with the PI controller.

Gpid = @(w) Kp*((1+w*Ki*1i)/(Ki*w*1i)*(1+Kd*w*1i)/(1+N*Kd*w*1i))*(C*(1i*w*eye(size(A))-A)^-1*B + D);
figure; plotBodeTransferFunction(G, maxFrequency);
plotBodeTransferFunction(Gpid, maxFrequency);
[gainMarginPID,phaseCrossoverPulsationPID,phaseMarginPID,gainCrossoverPulsationPID] = getStabilityCharacteristics(Gpid);
plotPhaseMargin(phaseMarginPID,gainCrossoverPulsationPID, maxFrequency);
subplot(2,1,1); legend("Plant","PID * Plant");

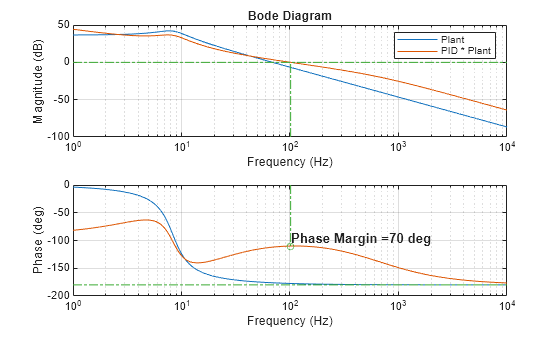
num = Kp*[Ki*Kd Ki+Kd 1];
den = [Ki*N*Kd Ki 0];
designDCMotorPIDControlPlotRPM("PID")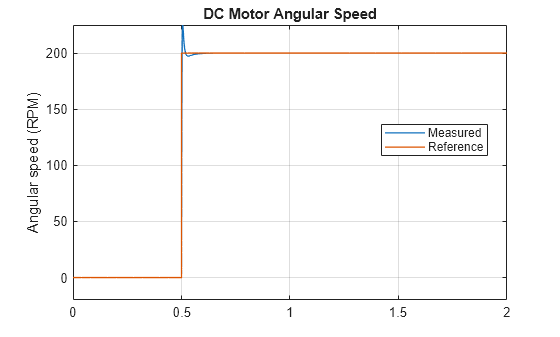

The PID controller significant improves the response time compared to the PI controller.