Design PI Controller for DC-DC Converter
This example shows how to design a PI controller for a DC-DC converter using classical control theory. Alternatively, you can use Steady State Manager, Model Linearizer, Frequency Response Estimator, or PID tuner apps to streamline the design.
To design the controller using concepts such as gain and phase margin, you need a linearized model. To learn how to linearize models with converters, see Linearize DC-DC Converter Model.
Model Overview
Open the DesignDCDCConverterControl model.
myModel = "DesignDCDCConverterControl";
open_system(myModel);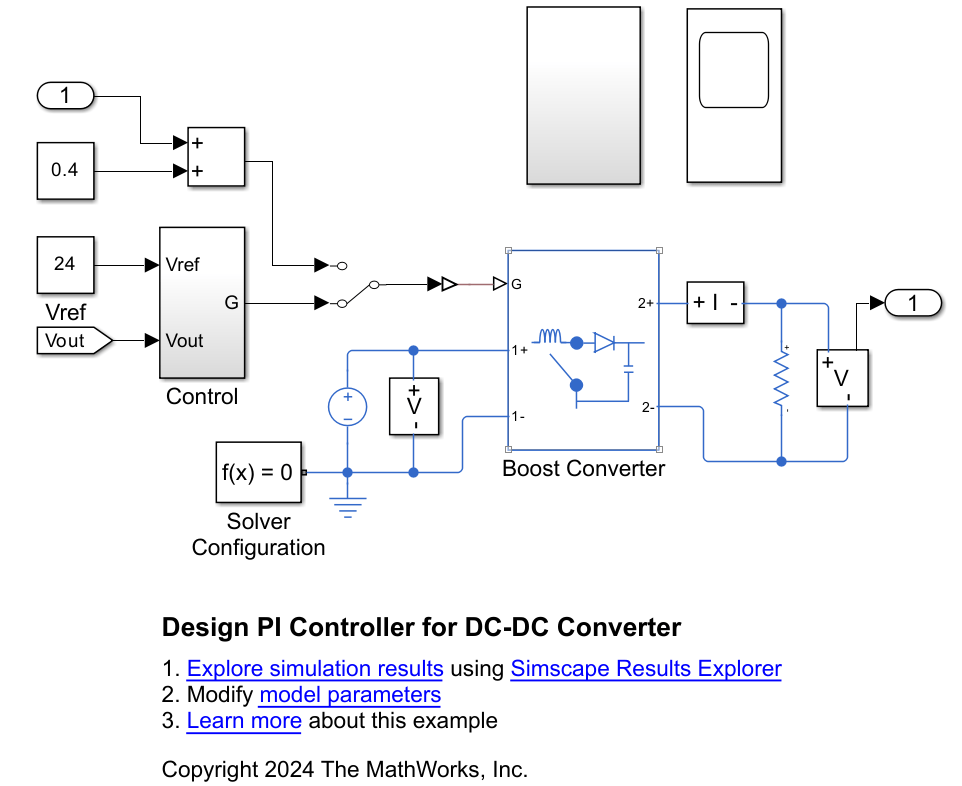
In this example, you model a boost converter using the Boost Converter block. The DC Voltage Source block supplies 12 V to the converter and the Constant or Control block specifies the duty cycle of the pulse-width modulation (PWM) input to the converter. The system can be run using a closed loop control or an open loop duty cycle reference.
Linearize Averaged Switching Model and Plot Frequency Response
Set up the model to allow linearization. Set the model to start from steady state and configure the inputs to run in open loop.
set_param(myModel + "/Solver Configuration",DoDC="on"); set_param(myModel + "/Manual Switch",sw="1");
Linearize the model using the linmod function.
[a,b,c,d] = linmod(myModel);
The transfer function is the Laplace transform of the impulse response of the system. This equation defines the transfer function in terms of the state-space matrices:
Compute the open-loop transfer function G from the state-space representation matrices A, B, C, and D.
G = @(w) c*(1i*w*eye(size(a))-a)^-1*b + d; figure; plotBodeTransferFunction(G)
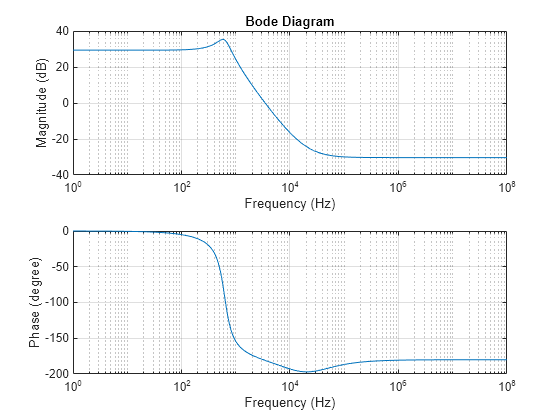
Compute Gain and Phase Margins
To calculate the phase margin, first obtain the frequency when the gain is 0 dB and calculate the phase at that frequency. To calculate the gain margin, bring the system to the verge of instability, which occurs at a phase angle of .
[gainMargindB,phaseCrossoverPulsation,phaseMargin,gainCrossoverPulsation] = getStabilityCharacteristics(G);
Plot the Bode diagram with stability margins.
figure; plotBodeTransferFunction(G) plotStabilityMargins(phaseMargin,gainCrossoverPulsation,gainMargindB,phaseCrossoverPulsation);
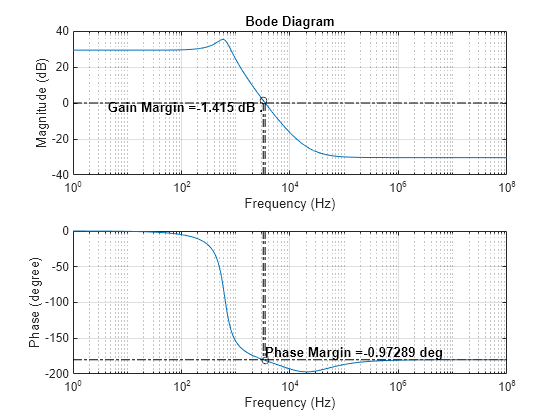
The phase and the gain margin are negative, which tells you that the plant is not stable.
Design Proportional Controller
A proportional controller changes the magnitude of the Bode plot but the phase remains the same. A typical gain margin is 5 dB. The gain margin is around -1.5 dB for the converter plant, so the proportional controller must decrease the gain by about 6.5 dB. The controller gain is therefore equal to the inverse of the gain margin plus the plant gain at phase crossover frequency.
Calculate the proportional controller gain.
gainMargindB = 5; % dB kpdB = - (gainMargindB + 20*log10(abs(G(phaseCrossoverPulsation)))); % dB Kp = 10^(kpdB/20);
Plot the new open-loop transfer function with the proportional control.
figure; plotBodeTransferFunction(G) Gp = @(w) Kp*(c*(1i*w*eye(size(a))-a)^-1*b + d); plotBodeTransferFunction(Gp);
Plot the Bode diagram with the stability margins.
[gainMarginP,phaseCrossoverPulsationP,phaseMarginP,gainCrossoverPulsationP] = getStabilityCharacteristics(Gp); plotStabilityMargins(phaseMarginP,gainCrossoverPulsationP,gainMarginP,phaseCrossoverPulsationP); subplot(2,1,1); legend("Plant","Kp * Plant");
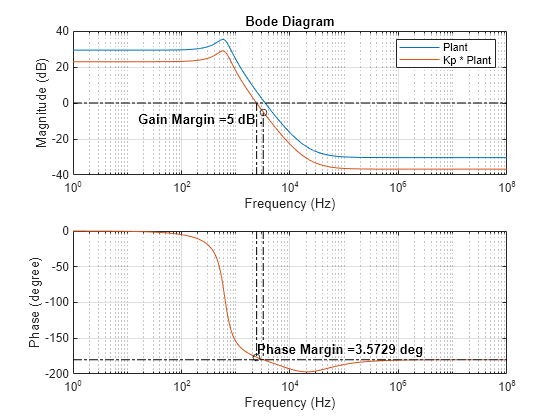
Both the phase and gain margins are positive. To verify that the system is now stable, plot the output voltage of the converter. The plot shows a steady-state error. If you calculate and take a look at the closed-loop transfer function, the order of the numerator and denominator polynomials is the same, which indicates a finite error at steady state for a step input.
plotOutputVoltage("P")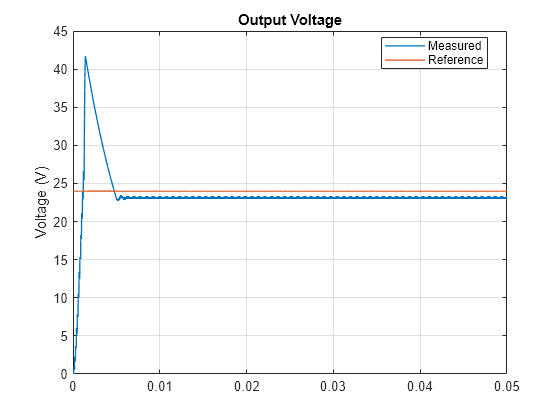
Design a Proportional Integral Controller
A proportional-integral controller changes both the gain and the phase of the open-loop Bode plot. The transfer function of the PI control is:
where:
is the proportional controller gain
is the integral control constant
is the Fourier transform variable
To calculate the gains analytically, use the following relation of the control gain and phase. From the Bode plot, decide the control gain and phase you need, and then use this expression to calculate the gains.
where:
is the amplitude of the control
is the phase of the control
is the variable expressed in the time domain
Choose the gain crossover frequency and phase margin and calculate the control parameters. A typical phase margin is between 45° and 60°. To have around –10° control phase shift, a crossover frequency of 700 Hz is a sensible value. For the phase margin, choose a value of 55°. Even though 700 Hz is close to the resonant frequency, a higher value makes it impossible to obtain a stable open-loop response.
phaseMarginPI = 55; % deg crossoverFreqPI = 700; % Hz
Calculate the control phase shift.
pulsationPI = crossoverFreqPI*2*pi; % rad/s angleGpulsationPI = angle(G(pulsationPI))/pi*180; % deg controlPhase = -180 + phaseMarginPI - angleGpulsationPI; % deg
Match the phases of both sides of the previous equation to obtain the value of .
; ;
If , then
I = pulsationPI/tand(90+controlPhase)
I = 712.3145
Calculate the gain of the plant at the gain crossover frequency and obtain the value of the proportional controller gain needed to have a 55° phase margin.
gainGpulsationPI = abs(G(pulsationPI)); controlGain = 1/gainGpulsationPI; Kp = controlGain*pulsationPI/sqrt(I+(pulsationPI)^2)
Kp = 0.0219
Plot the new open-loop transfer function with the PI controller.
Gpi = @(w) Kp*(I+w*1i)/(w*1i)*(c*(1i*w*eye(size(a))-a)^-1*b + d); figure; plotBodeTransferFunction(G); plotBodeTransferFunction(Gpi); [gainMarginPI,phaseCrossoverPulsationPI,phaseMarginPI,pulsationPI] = getStabilityCharacteristics(Gpi); plotStabilityMargins(phaseMarginPI,pulsationPI,gainMarginPI,phaseCrossoverPulsationPI); subplot(2,1,1); legend("Plant","PI * Plant");
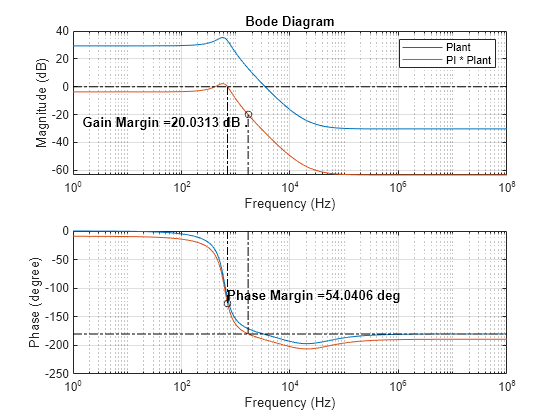
In this example, the gain margin is around 20 dB which is large enough to make the system controllable. If the gain margin is too small, you can choose different values of the gain crossover frequency and phase margin . The control is now slower due to the integral action, but the steady-state error is zero, and the overshoot is smaller.
plotOutputVoltage("PI")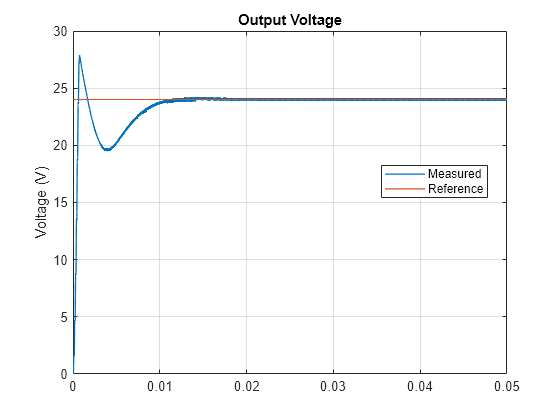
See Also
Boost Converter | Model Linearizer (Simulink Control Design) | PID Tuner (Control System Toolbox)
Topics
- Linearize DC-DC Converter Model
- Boost Converter Voltage Control
- Design Controller for Boost Converter Model Using Frequency Response Data (Simulink Control Design)
- Design Controller for Power Electronics Model Using Simulated I/O Data (Simulink Control Design)
- Design PID Control for DC Motor Using Classical Control Theory
- Linearize Models with Converters Using Averaged Switching