phasedelay
Phase delay of digital filter
Syntax
Description
[
returns the phi,w] = phasedelay(B,A,"ctf",n)n-point phase delay response of the digital filter
represented as Cascaded Transfer Functions (CTF) with numerator coefficients B and denominator coefficients
A. (since R2024b)
phasedelay(___) plots the phase
delay response versus frequency.
Examples
Input Arguments
Output Arguments
More About
Tips
Algorithms
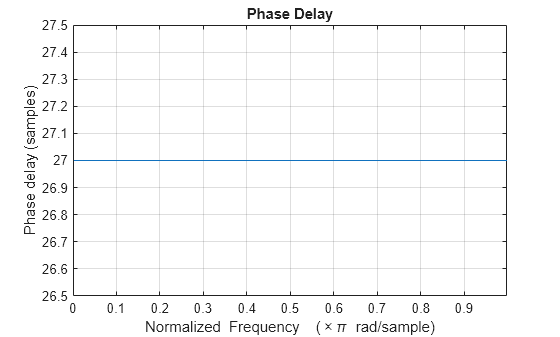
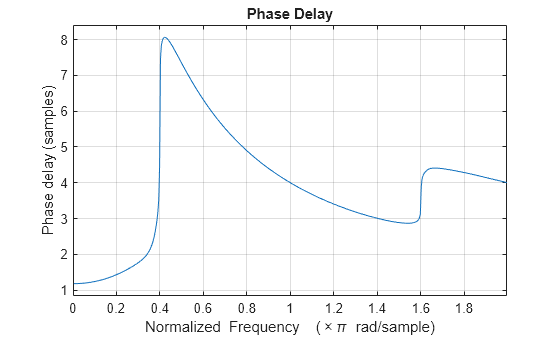
The phase delay response of a filter corresponds to the time delay
that each frequency component experiences as the input signal passes through the system. The
phasedelay function returns the phase delay response and the frequency
vector of the filter
given numerator and denominator coefficients in inputs
b and a.
References
[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.