wcgain

Worst-case gain of uncertain system

Syntax

[wcg,wcu] = wcgain(usys)

[wcg,wcu] = wcgain(usys,w)

[wcg,wcu] = wcgain(___,opts)

[wcg,wcu,info] = wcgain(___)

Description

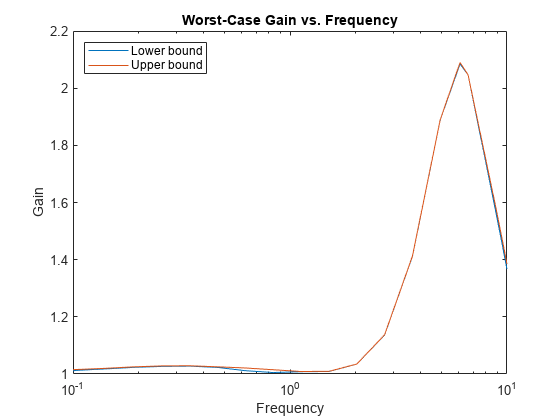
[wcg,wcu] = wcgain(usys) calculates the worst-case peak gain of the uncertain system usys. Peak gain refers to the maximum gain over frequency (H_∞ norm). For multi-input, multi-output (MIMO) systems, gain refers to the largest singular value of the frequency response matrix. (See sigma for more information about singular values.) The structure wcg contains upper and lower bounds on the worst-case gain and the critical frequency at which the lower bound peaks. (See Worst-Case Gain.) The structure wcu contains the values of the uncertain elements of usys that cause the worst-case peak gain.

[wcg,wcu] = wcgain(usys,w) restricts worst-case computation to the frequencies specified by w.

• If w is a cell array of the form {wmin,wmax}, then wcgain returns the worst-case gain in the interval between wmin and wmax.

• If w is a vector of frequencies, then wcgain calculates the worst-case gain at the specified frequencies only, and returns the worst of those gains.

[wcg,wcu] = wcgain(___,opts) specifies additional options for the computation. Use wcOptions to create opts. You can use this syntax with any of the previous input-argument combinations.

[wcg,wcu,info] = wcgain(___) returns a structure with additional information about the worst-case gains and the perturbations that generate them. See info for details about this structure. You can use this syntax with any of the previous input-argument combinations.

Examples

Worst-Case Peak Gain of Closed-Loop System

Consider a control system whose plant is nominally an integrator with some additive dynamic uncertainty. Create a model of the plant.

delta = ultidyn('delta',[1 1],'bound',0.4); 
G = tf(1,[1 0]) + delta;

Create a PD controller for the model. Suppose you want to examine the worst-case disturbance rejection performance. Build the closed-loop sensitivity function to examine the worst-case gain of a disturbance at the plant input.

C = pid(2,0,-0.04,0.02);
S = feedback(1,G*C);

Because of the uncertainty, the frequency response of this transfer function falls within some envelope. The frequency-response magnitude of a few samples of the system gives a sense of that envelope.

bodemag(S)

Each sample has a different peak gain. Find the highest peak-gain value within the envelope and the corresponding values for the uncertain elements.

[wcg,wcu] = wcgain(S);
wcg

wcg = struct with fields:
           LowerBound: 5.1036
           UpperBound: 5.1140
    CriticalFrequency: 10.7241

The LowerBound and UpperBound fields of wcg show that the worst-case peak gain is around 5.1. This gain occurs at the critical frequency around 10.6 rad/s.

The output wcu is a structure that contains the perturbation to delta that causes the worst-case gain. Confirm the result by substituting this value into the sensitivity function.

Swc = usubs(S,wcu);
getPeakGain(Swc)

ans = 
5.1037

Because the system has dynamic uncertainty delta with gain not exceeding 0.4, the worst-case value of delta should be a system with peak gain of 0.4. Confirm this result.

getPeakGain(wcu.delta)

ans = 
0.4000

Worst-Case Gain at Frequencies in a Range

Consider a model of a control system containing uncertain elements.

k = ureal('k',10,'Percent',40);
delta = ultidyn('delta',[1 1]); 
G = tf(18,[1 1.8 k]) * (1 + 0.5*delta);
C = pid(2.3,3,0.38,0.001);
CL = feedback(G*C,1);

By default, wcgain returns only the worst-case peak gain over all frequencies. To obtain worst-case gain values at multiple frequencies, use the 'VaryFrequency' option of wcOptions. For example, compute the highest possible gain of the system at frequency points between 0.1 and 10 rad/s.

opts = wcOptions('VaryFrequency','on');
[wcg1,wcu1,info1] = wcgain(CL,{0.1,10},opts);
info1

info1 = struct with fields:
                 Model: 1
             Frequency: [19x1 double]
                Bounds: [19x2 double]
     WorstPerturbation: [19x1 struct]
           Sensitivity: [1x1 struct]
    BadUncertainValues: [19x1 struct]
            ArrayIndex: 1

wcgain returns the vector of frequencies in the info output, in the Frequencies field. info.Bounds contains the upper and lower bounds on the worst-case gain at each frequency. Use these values to plot the frequency dependence of the worst-case gain.

semilogx(info1.Frequency,info1.Bounds)
title('Worst-Case Gain vs. Frequency')
ylabel('Gain')
xlabel('Frequency')
legend('Lower bound','Upper bound','Location','northwest')

The curve shows the high-gain envelope for all systems within the uncertainty ranges of CL. You can also use wcsigmaplot to plot this envelope along with samples of the system.

When you use the 'VaryFrequency' option, wcgain chooses frequency points automatically. The frequencies it selects are guaranteed to include the frequency at which the worst-case gain is highest (within the specified range). Display the returned frequency values to confirm that they include the critical frequency.

info1.Frequency

ans = 19×1

    0.1000
    0.1061
    0.1425
    0.1914
    0.2572
    0.3455
    0.4642
    0.6236
    0.8377
    1.1253
      ⋮

wcg1.CriticalFrequency

ans = 
6.0746

Alternatively, instead of using 'VaryFrequency', you can specify particular frequencies at which to compute the worst-case gains. info.Bounds contains the worst-case gains at all specified frequencies.

w = logspace(-1,1,24); 
[wcg2,wcu2,info2] = wcgain(CL,w);
semilogx(w,info2.Bounds)
title('Worst-Case Gain vs. Frequency')
ylabel('Gain')
xlabel('Frequency')
legend('Lower bound','Upper bound','Location','northwest')

When you provide the frequency grid in this way, the results are not guaranteed to include the overall worst-case gain, which might fall between specified frequency points. To see this, examine wcg1 and wcg2, which contain the bounds for the two approaches.

wcg1

wcg1 = struct with fields:
           LowerBound: 2.0848
           UpperBound: 2.0897
    CriticalFrequency: 6.0746

wcg2

wcg2 = struct with fields:
           LowerBound: 2.0349
           UpperBound: 2.0370
    CriticalFrequency: 6.7002

wcg1, computed using VaryFrequency, finds a higher peak gain than the specified frequency grid.

Determine Effect of Uncertainty Range on Worst-Case Response

Consider a feedback loop with a first-order plant and a PI controller. The time constant of the plant is uncertain, and the feedback loop accounts for unmodeled dynamic uncertainty. Compute the worst-case gain of the sensitivity function Si at the plant inputs. Use the 'Sensitivity' option of wcOptions to compute how sensitive this worst-case gain is to each uncertain element.

% Create uncertain system and controller
delta = ultidyn('delta',[1 1]);
tau = ureal('tau',5,'range',[4 6]);
P = tf(1,[tau 1])*(1+0.25*delta);
C = pid(4,4);

opt = wcOptions('Sensitivity','on');
Si = inv(1 + C*P);
[wcg,~,info] = wcgain(Si,opt);

The Sensitivity field of the info output structure includes data that reflects how much the maximum gain of the input sensitivity function changes with each uncertain element.

info.Sensitivity

ans = struct with fields:
    delta: 44
      tau: 9

This result tells you that if the uncertainty range of delta increases by 10%, the peak input sensitivity increases by about 4.4%. Similarly, a 10% increase in the uncertainty range of tau causes about a 0.9% increase in the peak input sensitivity.

Improve Worst-Case Perturbation

Specifying certain options for the structured-singular-value computation that underlies the worst-gain computation can yield better results in some cases. For example, consider a sample plant and controller.

load('wcgExampleData.mat')

This command loads gPlant, a MIMO plant with 10 outputs, 8 inputs, and 11 uncertain elements. It also loads Kmu, a state-space controller model. Form a closed-loop system with these models, and examine the worst-case gain.

CL = lft(gPlant,Kmu);
[wcg,wcu] = wcgain(CL);
wcg

wcg = struct with fields:
           LowerBound: 10.8742
           UpperBound: 11.2135
    CriticalFrequency: 6.6794

There is a large difference between the lower and upper bounds on the worst-case gain. To get a better estimate of the actual worst-case gain, increase the number of restarts that wcgain uses for computing of the worst-case perturbation and associated lower bound. Doing so can result in a tighter lower bound. This option does not affect the upper-bound calculation.

opt = wcOptions('MussvOptions','m3');
[wcg,wcu] = wcgain(CL,opt);
wcg

wcg = struct with fields:
           LowerBound: 10.8742
           UpperBound: 11.2135
    CriticalFrequency: 6.6794

The difference between the lower bound and upper bound on the worst-case gain is much smaller. The critical frequency is different as well.

Input Arguments

usys — Dynamic system with uncertainty

uss | ufrd | genss | genfrd

Dynamic system with uncertainty, specified as a uss, ufrd, genss, or genfrd model that contains uncertain elements. For genss or genfrd models, wcgain uses the current value of any tunable blocks and folds them into the known (not uncertain) part of the model.

usys can also be an array of uncertain models. In that case, wcgain returns the worst-case gain across all models in the array, and the info output contains the index of the corresponding model.

w — Frequencies

{wmin,wmax} | vector

Frequencies at which to compute worst-case gains, specified as the cell array {wmin,wmax} or as a vector of frequency values.

• If w is a cell array of the form {wmin,wmax}, then the function returns the worst-case gain in the interval between wmin and wmax.

• If w is a vector of frequencies, then the function computes the worst-case gain at each specified frequency.

Specify frequencies in units of rad/TimeUnit, where TimeUnit is the TimeUnit property of the model.

opts — Options for margin computation

wcOptions object

Options for worst-case computation, specified as an object you create with wcOptions. The available options include settings that let you:

• Extract frequency-dependent worst-case gains (see Worst-Case Gain).

• Examine the sensitivity of the worst-case gain to each uncertain element.

• Improve the results of the worst-case gain calculation by setting certain options for the underlying mussv calculation. For an example, see Improve Worst-Case Perturbation.

For more information about all available options, see wcOptions.

Example: wcOptions('Sensitivity','on','MussvOptions','m3')

Output Arguments

wcg — Worst-case peak gain and critical frequency

structure

Worst-case peak gain and critical frequency, returned as a structure containing the following fields:

Field	Description
LowerBound	Lower bound on the actual worst-case peak gain of the model, returned as a scalar value. This value is the peak gain corresponding to the worst-case perturbation wcu. The exact worst-case peak gain is guaranteed to be no smaller than LowerBound.
UpperBound	Upper bound on the actual worst-case peak gain of the model, returned as a scalar value. The exact worst-case peak gain is guaranteed to be no larger than UpperBound. When you specify a frequency grid as a vector w, the guarantee only applies at the specified frequencies.
CriticalFrequency	Frequency at which the worst-case peak gain occurs, in rad/TimeUnit, where TimeUnit is the TimeUnit property of usys.

wcu — Worst-case perturbation

structure

Worst case perturbation of uncertain elements, returned as a structure whose fields are the names of the uncertain elements of usys. Each field contains the actual value of the corresponding uncertain element of usys when the worst-case peak gain occurs. For example, if usys includes an uncertain matrix M and SISO uncertain dynamics delta, then wcu.M is a numeric matrix and wcu.delta is a SISO state-space model.

Use usubs(usys,wcu) to substitute these values for the uncertain elements in usys, to obtain the dynamic system that has the worst-case peak gain.

info — Additional information about worst-case values

structure

Additional information about the worst-case values, returned as a structure with the following fields:

Field	Description
Model	Index of the model that has the largest worst-case peak gain, when usys is an array of models.
Frequency	Frequency points at which wcgain returns the worst-case gain, returned as a vector. If the 'VaryFrequency' option of wcOptions is 'off', then info.Frequency is the critical frequency, the frequency at which the worst-case peak gain occurs. If the largest lower bound and the smallest upper bound on the worst-case gain occur at different frequencies, then info.Frequency is a vector containing these two frequencies. If the 'VaryFrequency' option of wcOptions is 'on', then info.Frequency contains the frequencies selected by wcgain. These frequencies are guaranteed to include the frequency at which the worst-case peak gain occurs. If you specify a vector of frequencies w at which to compute the worst-case gains, then info.Frequency = w. When you specify a frequency vector, these frequencies are not guaranteed to include the frequency at which the worst-case peak gain occurs. The 'VaryFrequency' option is meaningful only for uss and genss models. wcgain ignores the option for ufrd and genfrd models.
Bounds	Lower and upper bounds on the actual worst-case gain of the model, returned as an array. info.Bounds(:,1) contains the lower bound at each corresponding frequency in info.Frequency, and info.Bounds(:,2) contains the corresponding upper bounds.
WorstPerturbation	Perturbations that cause the worst-case gain at each frequency point in info.Frequency, returned as a structure array. The fields of info.WorstPerturbation are the names of the uncertain elements in usys, and each field contains the worst-case value of the corresponding element at each frequency. For example, if usys includes an uncertain parameter p and SISO uncertain dynamics delta, then info.WorstPerturbation.p is a collection of numeric values and info.WorstPerturbation.delta is a collection of SISO state-space models.
Sensitivity	Sensitivity of the worst-case gain to each uncertain element, returned as a structure when the 'Sensitivity' option of wcOptions is 'on'. The fields of info.Sensitivity are the names of the uncertain elements in usys. Each field contains a percentage that measures how much the uncertainty in the corresponding element affects the worst-case gain. For example, if info.Sensitivity.p is 50, then a given fractional change in the uncertainty range of p causes half as much fractional change in the worst-case gain. If the 'Sensitivity' option of wcOptions is off (the default setting), then info.Sensitivity is NaN.
BadUncertainValues	Same as WorstPerturbation. Included for compatibility with R2016a and earlier.
ArrayIndex	Same as Model. Included for compatibility with R2016a and earlier.

More About

Worst-Case Gain

By default, wcgain returns the peak gain (or peak singular value, for MIMO systems) achievable within the uncertainty range, over all frequencies (or the frequencies specified by w). You can obtain the peak gain as a function of frequency using the VaryFrequency option of wcOptions.

To understand the difference, consider the following illustration, representing the magnitude of the frequency response of an uncertain system.

The dark blue curve is the nominal response of the system. The light blue curves show various sampled responses of the system. The wcg output of wcgain contains the bounds on the worst-case gain over all frequencies, about 5 dB in the illustration. The frequency at which this gain occurs is the critical frequency, also returned in wcg.

If you set the VaryFrequency option of wcOptions to 'on', then wcgain also calculates the maximum gain at each frequency point, shown by the red curve. wcgain returns these values in info.Bounds. See Worst-Case Gain at Frequencies in a Range for an example. You can also use wcsigmaplot to visualize the worst-case gain as a function of frequency.

Algorithms

Computing the worst-case gain at a particular frequency is equivalent to computing the structured singular value, μ, for some appropriate block structure (μ-analysis).

For uss and genss models, wcgain(usys) and wcgain(usys,{wmin,wmax}) use an algorithm that finds the worst-case gain across frequency. This algorithm does not rely on frequency gridding and is not adversely affected by sharp peaks of the μ structured singular value. See Getting Reliable Estimates of Robustness Margins for more information.

For ufrd and genfrd models, wcgain computes the μ lower and upper bounds at each frequency point. This computation offers no guarantee between frequency points and can be inaccurate if the uncertainty gives rise to sharp resonances. The syntax wcgain(uss,w), where w is a vector of frequency points, is the same as wcgain(ufrd(uss,w)) and also relies on frequency gridding to compute the worst-case gain.

In general, the algorithm for state-space models is faster and safer than the frequency-gridding approach. In some cases, however, the state-space algorithm requires many μ calculations. In those cases, specifying a frequency grid as a vector w can be faster, provided that the worst-case gain varies smoothly with frequency. Such smooth variation is typical for systems with dynamic uncertainty.

Version History

Introduced before R2006a