Getting Reliable Estimates of Robustness Margins
This example illustrates the pitfalls of using frequency gridding to compute robustness margins for systems with only real uncertain parameters. It presents a safer approach along with ways to mitigate discontinuities in the structured singular value .
How Discontinuities Can Hide Robustness Issues
Consider a spring-mass-damper system with 100% parameter uncertainty in the damping coefficient and 0% uncertainty in the spring coefficient. Note that all uncertainty is of ureal type.
m = 1; k = 1; c = ureal('c',1,'plusminus',1); sys = tf(1,[m c k]);
As the uncertain element c varies, the only place where the poles can migrate from stable to unstable is at s = j*1 (1 rad/sec). No amount of variation in c can cause them to migrate across the jw-axis at any other frequency. As a result, the robust stability margin is infinite at all frequencies except 1 rad/s, where the margin with respect to the specified uncertainty is 1. In other words, the robust stability margin and the underlying structured singular value are discontinuous as a function of frequency.
The traditional approach to computing the robust stability margin is to pick a frequency grid and compute lower and upper bounds for at each frequency point. Under most conditions, the robust stability margin is continuous with respect to frequency and this approach gives good estimates provided you use a sufficiently dense frequency grid. However in problems with only ureal uncertainty, such as the example above, poles can migrate from stable to unstable only at specific frequencies (the points of discontinuity for ), so any frequency grid that excludes these particular frequencies will lead to over-optimistic stability margins.
To see this effect, pick a frequency grid for the spring-mass-damper system above and compute the robust stability margins at these frequency points using robstab.
omega = logspace(-1,1,40); % one possible grid
[stabmarg,wcu,info] = robstab(sys,omega);
stabmargstabmarg = struct with fields:
LowerBound: 5.0348e+03
UpperBound: Inf
CriticalFrequency: 0.1000
The field info.Bounds gives the margin lower and upper bounds at each frequency. Verify that the lower bound (the guaranteed margin) is large at all frequencies.
loglog(omega,info.Bounds(:,1))
title('Robust stability margin: 40 frequency points')
Note that making the grid denser would not help. Only by adding f=1 to the grid will we find the true margin.
f = 1; stabmarg = robstab(sys,f)
stabmarg = struct with fields:
LowerBound: 1.0000
UpperBound: 1
CriticalFrequency: 1
Safe Computation of Robustness Margins
Rather than specifying a frequency grid, apply robstab directly to the USS model sys. This uses a more advanced algorithm that is guaranteed to find the peak of even in the presence of a discontinuity. This approach is more accurate and often faster than frequency gridding.
[stabmarg,wcu] = robstab(sys)
stabmarg = struct with fields:
LowerBound: 1.0000
UpperBound: 1.0000
CriticalFrequency: 1.0000
wcu = struct with fields:
c: 2.2204e-16
This computes the correct robust stability margin (1), identifies the critical frequency (f=1), and finds the smallest destabilizing perturbation (setting c=0, as expected).
Modifying the Uncertainty Model to Eliminate Discontinuities
The example above shows that the robust stability margin can be a discontinuous function of frequency. In other words, it can have jumps. We can eliminate such jumps by adding a small amount of uncertain dynamics to every uncertain real parameter. This amounts to adding some dynamics to pure gains. Importantly, as the size of the added dynamics goes to zero, the estimated margin for the modified problem converges to the true margin for the original problem.
In the spring-mass-damper example, we model c as a ureal with the range [0.05,1.95] rather than [0,2], and add a ultidyn perturbation with gain bounded by 0.05. This combination covers the original uncertainty in c and introduces only 5% conservatism.
cc = ureal('cReal',1,'plusminus',0.95) + ultidyn('cUlti',[1 1],'Bound',0.05); sysreg = usubs(sys,'c',cc);
Recompute the robust stability margin over the frequency grid omega.
[stabmarg,~,info] = robstab(sysreg,omega); stabmarg
stabmarg = struct with fields:
LowerBound: 2.3624
UpperBound: 2.3630
CriticalFrequency: 1.0608
Now the frequency-gridded calculation yields a margin of 2.36. This is still greater than 1 (the true margin) because the density of frequency points is not high enough. Increase the number of points from 40 to 200 and recompute the margin.
OmegaDense = logspace(-1,1,200); [stabmarg,~,info] = robstab(sysreg,OmegaDense); stabmarg
stabmarg = struct with fields:
LowerBound: 1.0026
UpperBound: 1.0056
CriticalFrequency: 0.9885
Plot the robustness margin as a function of frequency.
loglog(OmegaDense,info.Bounds(:,1),OmegaDense,info.Bounds(:,2)) title('Robust stability margin: 5% added dynamics, 200 frequency points') legend('Lower bound','Upper bound')
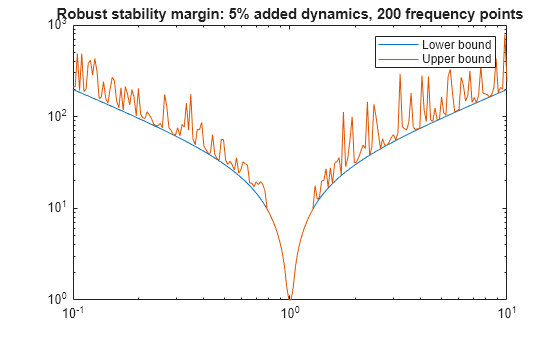
The computed margin is now close to 1, the true margin for the original problem. In general, the stability margin of the modified problem is less than or equal to that of the original problem. If it is significantly less, then the answer to the question "What is the stability margin?" is very sensitive to the uncertainty model. In this case, we put more faith in the value that allows for a few percents of unmodeled dynamics. Either way, the stability margin for the modified problem is more trustworthy.
Automated Regularization of Discontinuous Problems
The command complexify automates the procedure of replacing a ureal with the sum of a ureal and ultidyn. The analysis above can be repeated using complexify obtaining the same results.
sysreg = complexify(sys,0.05,'ultidyn');
[stabmarg,~,info] = robstab(sysreg,OmegaDense);
stabmargstabmarg = struct with fields:
LowerBound: 1.0026
UpperBound: 1.0056
CriticalFrequency: 0.9885
Note that such regularization is only needed when using frequency gridding. Applying robstab directly to the original uncertain model sys yields the correct margin without frequency gridding or need for regularization.
References
The continuity of the robust stability margin, and the subsequent computational and interpretational difficulties raised by the presence of discontinuities are considered in [1]. The consequences and interpretations of the regularization illustrated in this small example are described in [2]. An extensive analysis of regularization for 2-parameter example is given in [2].
[1] Barmish, B.R., Khargonekar, P.P, Shi, Z.C., and R. Tempo, "Robustness margin need not be a continuous function of the problem data," Systems & Control Letters, Vol. 15, No. 2, 1990, pp. 91-98.
[2] Packard, A., and P. Pandey, "Continuity properties of the real/complex structured singular value," Vol. 38, No. 3, 1993, pp. 415-428.
See Also
robstab | diskmargin | wcdiskmargin