ncfmargin
Calculate normalized coprime stability margin of plant-controller feedback loop
Description
[
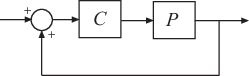
returns the normalized coprime stability margin of the multivariable feedback loop
consisting of a controller marg,freq] = ncfmargin(P,C)C in negative feedback with a plant
P:

The normalized coprime robust stability margin (also called the gap metric stability margin) is an indication of robustness to unstructured perturbations. Values greater than 0.3 generally indicate good robustness margins.
[
specifies the sign of the feedback connection assumed for the margin calculation. By
default, marg,freq] = ncfmargin(P,C,sign)sign = -1. Set sign = +1 for
positive-feedback interconnection.
[
calculates the normalized coprime factor metric with the specified relative accuracy.marg,freq] = ncfmargin(___,tol)
Examples
Input Arguments
Output Arguments
More About
Tips
While
ncfmarginassumes a negative-feedback loop, thencfsyncommand designs a controller for a positive-feedback loop. Therefore, to compute the margin using a controller designed withncfsyn, use[marg,freq] = ncfmargin(P,C,+1).
Algorithms
The computation of the normalized coprime stability margin is as described in Chapter 16 of [1].
References
[1] Zhou, K., Doyle, J.C., Essentials of Robust Control. London, UK: Pearson, 1997.
Version History
Introduced before R2006a
See Also
ncfsyn | robstab | diskmargin | gapmetric | wcdiskmargin