ncfsyn
Loop shaping design using Glover-McFarlane method
Syntax
Description
ncfsyn implements a method for designing controllers that
uses a combination of loop shaping and robust stabilization as proposed in [1]-[2]. The function computes the Glover-McFarlane H∞
normalized coprime factor loop-shaping controller K for a plant
G with pre-compensator and post-compensator weights
W1 and
W2. The function assumes the positive feedback
configuration of the following illustration.
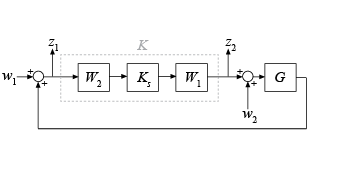
To specify negative feedback, replace G by –G. The
controller Ks stabilizes a family of systems given
by a ball of uncertainty in the normalized coprime factors of the shaped plant Gs =
W2GW1. The final controller K returned by
ncfsyn is obtained as K =
W1KsW2.
[
computes the Glover-McFarlane H∞ normalized
coprime factor loop-shaping controller K,CL,gamma,info] = ncfsyn(G)K for the plant
G, with W1 =
W2 = I. CL is the closed-loop system from the disturbances
w1 and
w2 to the outputs
z1 and
z2. The function also returns the
H∞ performance gamma, and a
structure containing additional information about the result.
Examples
Input Arguments
Output Arguments
Tips
While
ncfmarginassumes a negative-feedback loop, thencfsyncommand designs a controller for a positive-feedback loop. Therefore, to compute the margin using a controller designed withncfsyn, use[marg,freq] = ncfmargin(G,K,+1).
Algorithms
The returned controller K = W1KsW2, where Ks is an optimal H∞ controller that minimizes the H∞ cost
The optimal performance is the minimal cost
Suppose that Gs=NM–1, where N(jω)*N(jω) + M(jω)*M(jω) = I, is a normalized coprime factorization (NCF) of the weighted plant model Gs. Then, theory ensures that the control system remains robustly stable for any perturbation to Gs of the form
where Δ1, Δ2 are a stable pair satisfying
The closed-loop H∞-norm objective has the standard signal gain interpretation. Finally it can be shown that the controller, Ks, does not substantially affect the loop shape in frequencies where the gain of W2GW1 is either high or low, and will guarantee satisfactory stability margins in the frequency region of gain cross-over. In the regulator set-up, the final controller to be implemented is K=W1KsW2.
References
[1] McFarlane, Duncan C., and Keith Glover, eds. Robust Controller Design using Normalized Coprime Factor Plant Descriptions. Vol. 138. Lecture Notes in Control and Information Sciences. Berlin/Heidelberg: Springer-Verlag, 1990. https://doi.org/10.1007/BFb0043199.
[2] McFarlane, D., and K. Glover, “A Loop Shaping Design Procedure using H∞ Synthesis,” IEEE Transactions on Automatic Control, no. 6 (June 1992): pp. 759–69. https://doi.org/10.1109/9.256330.
[3] Vinnicombe, Glenn. “Measuring Robustness of Feedback Systems.” PhD Dissertation, University of Cambridge, 1992.
[4] Zhou, Kemin, and John Comstock Doyle. Essentials of Robust Control. Upper Saddle River, NJ: Prentice-Hall, 1998.