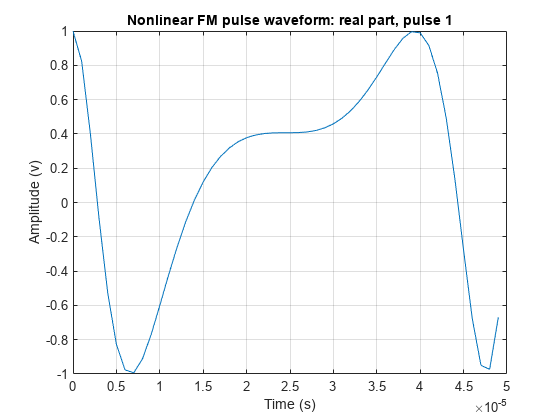
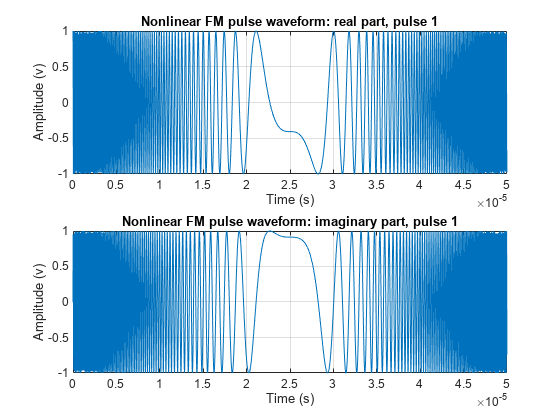
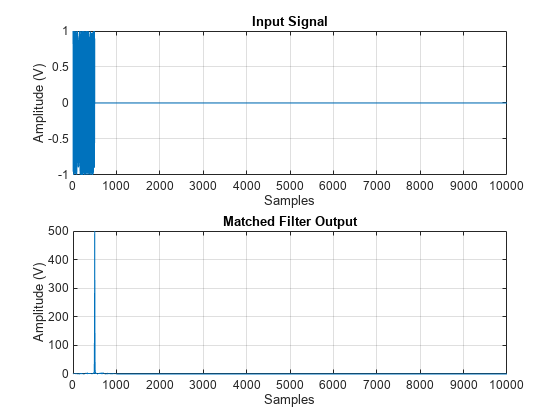
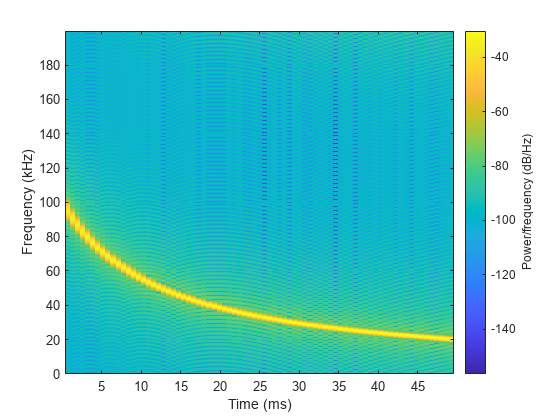
phased.NonlinearFMWaveform

Nonlinear FM pulse waveform

Since R2023a

Description

The phased.NonlinearFMWaveform System object™ creates a frequency-modulated waveform whose frequency is a nonlinear function of time (NLFM). NLFM waveforms achieve low-range sidelobes by shaping the spectrum using frequency modulation. Four different waveforms are supported depending on the FrequencyModulation property:

• 'Polynomial' – Generate a waveform with an instantaneous frequency that follows a polynomial function.

• 'Hyperbolic' – Generate a hyperbolic frequency modulated (HFM) waveform.

• 'Hybrid Linear-Tangent' – Generate a hybrid NLFM waveform that combines an LFM waveform with tan-FM waveform.

• 'Stepped Price' – Generate a stepped version of Price's NLFM waveform.

To create the waveforms:

1. Create the phased.NonlinearFMWaveform object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

waveform = phased.NonlinearFMWaveform

waveform = phased.NonlinearFMWaveform(Name = Value)

Description

waveform = phased.NonlinearFMWaveform creates a nonlinear FM pulse waveform System object. By default, the waveform has a polynomial frequency modulation.

waveform = phased.NonlinearFMWaveform(Name = Value) creates a nonlinear FM pulse waveform System object with each specified property Name set to the specified Value. You can specify additional name-value pair arguments in any order as (Name1 = Value1,...,NameN = ValueN).

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

SampleRate — Signal sample rate

1e6 (default) | positive scalar

Signal sample rate, specified as a positive scalar. The ratio of sample rate to pulse repetition frequency must be a positive integer, so the number of samples in each pulse must be an integer value. Units are in Hertz.

Example: 100e3

Data Types: double

DurationSpecification — Method to set pulse duration

'Pulse width' (default) | 'Duty cycle'

Method to set pulse duration (pulse width), specified as 'Pulse width' or 'Duty cycle'. This property determines how you set the pulse duration.

• When you set this property to 'Pulse width', set the pulse duration directly using the PulseWidth property.

• When you set this property to 'Duty cycle', set the pulse duration from the values of the PRF and DutyCycle properties. The pulse width is equal to the value of the DutyCycle property divided by the value of the PRF property.

Data Types: char | string

PulseWidth — Pulse time duration

50e-6 (default) | positive scalar

Pulse time duration, specified as a positive scalar. The value must satisfy PulseWidth <= 1./PRF. Units are in seconds.

Dependencies

To enable this property, set the DurationSpecification property to 'Pulse width'.

Data Types: double

DutyCycle — Pulse duty cycle

0.5 (default) | positive scalar in the range [0,1]

Pulse duty cycle, specified as a positive scalar in the range [0,1]. The pulse width is the value of the DutyCycle property divided by the value of the PRF property. This quantity is dimensionless.

Example: 0.75

Dependencies

To enable this property, set the DurationSpecification property to 'Duty cycle'.

Data Types: double

PRF — Pulse repetition frequency

10e3 (default) | positive scalar | row vector of positive values

Pulse repetition frequency (PRF), specified as a scalar or a row vector. Units are in Hz. The pulse repetition interval (PRI) is the inverse of the pulse repetition frequency PRF value. The PRF must satisfy these restrictions:

• The product of PRF and PulseWidth must be less than or equal to one. This condition requires that the pulse width is less than one PRI. For the phase-coded waveform, the pulse width is the product of the values of the ChipWidth and NumChips properties.

• The ratio of SampleRate to PRF must be an integer. This condition requires that the number of samples in one PRI is an integer.

You can set the value of PRF using the PRF property settings alone or using property settings in conjunction with the prfidx input argument of the object.

• When PRFSelectionInputPort is false, you set the PRF using the PRF properties alone. You can:

  • Implement a constant PRF by specifying the PRF property as a positive real-valued scalar.

  • Implement a staggered PRF by specifying the PRF property as a row vector with positive real-valued elements. Each call to the object uses successive elements of this vector as the PRF. Once the object reaches the last element of the vector, it continues the process cyclically with the first element of the vector.

• When PRFSelectionInputPort is true, you can set the PRF value using the PRF property in conjunction with the prfidx input argument. You implement a selectable PRF by specifying the PRF property as a row vector with positive real-valued elements. When you execute the object, the object selects a PRF by using the index you specify in the prfidx input argument to index into the PRF vector.

In all cases, the number of output samples is fixed when you set the OutputFormat property to 'Samples'. When you use a varying PRF and also set the OutputFormat property to 'Pulses', the number of samples can vary.

Data Types: double

PRFSelectionInputPort — Enable PRF selection input

false (default) | true

Enable PRF selection input, specified as false or true. When you set this property to true, you can pass an index argument to the object to select a predefined value from the PRF property vector. When you set this property to false, the object uses the PRF property to define the PRF sequence used in the simulation.

Data Types: logical

FrequencyModulation — Frequency modulation

'Polynomial' (default) | 'Hyperbolic' | 'Hybrid Linear-Tangent' | 'Stepped Price'

Frequency modulation of the nonlinear FM waveform, specified as 'Polynomial' , 'Hyperbolic', 'Hybrid Linear-Tangent', or 'Stepped Price'.

• When you set the property to 'Polynomial' the System object generates a waveform with an instantaneous frequency that follows a polynomial function. You specify the coefficients in the PolynomialCoefficients property. The object normalizes the resulting frequency function such that each pulse sweeps the bandwidth you specify in SweepBandwidth. The SweepDirection property is inactive when FrequencyModulation is set to 'Polynomial''.

• When you set the property to 'Hyperbolic' the System object generates a hyperbolic frequency modulated (HFM) waveform. Use the HyperbolicStartFrequency property to set the start frequency of the hyperbolic sweep. The SweepInterval property is inactive in this case.

• When you set the property to 'Hybrid Linear-Tangent' System object generates a hybrid NLFM waveform that combines an LFM with a tan-FM as described by Collins and Atkins [1]. You specify the balance between LFM and tan-FM in the LinearTangentBalance property, and the portion of the tan(x) curve to used for tan-FM in the TangentCurvePortion property.

• When you set the property to 'Stepped Price' the System object generates a stepped version of the Price's NLFM waveform as given by Levanon and Mozeson [2]. The SweepBandwidth property is inactive in this case and the sweep bandwidth is determined by the bandwidth factors in the BandwidthFactors property and the number of frequency steps in the NumSteps property.

Example: 'Stepped Price'

Data Types: char | string

PolynomialCoefficients — Coefficients of polynomial frequency function

[1 0 0] (default) | (N+1)-length real-valued vector

Coefficients of the polynomial frequency function, specified as a length-(N+1) real-valued vector. The vector represents the coefficients of an N-th degree polynomial. The first entry in PolynomialCoefficients is the coefficient of the highest power N of the polynomial. The last entry is the coefficient of the power zero term of the polynomial.

Example: [0.5,1,1,0.5]

Dependencies

To enable this property, set the FrequencyModulation property to 'Polynomial'.

Data Types: double

LinearTangentBalance — Balance factor between linear FM and tan-FM functions

0.5 (default) | positive scalar

Balance factor between linear FM and tan-FM functions for a hybrid linear-tangent NLFM waveform, specified as a scalar. Units are dimensionless.

Example: 0.66

Dependencies

To enable this property, set the FrequencyModulation property to 'Hybrid Linear-Tangent'.

Data Types: double

TangentCurvePortion — Portion of tan(x) curve

1.4 (default) | real-valued scalar

Portion of the tan(x) curve between -π/2 and +π/2 to use as a tangent term in the hybrid linear-tangent FM frequency function, specified as a scalar between 0 and +π/2.

Example: 1.2

Dependencies

To enable this property, set the FrequencyModulation property to 'Hybrid Linear-Tangent'.

Data Types: double

NumSteps — Number of frequency steps

50 (default) | positive integer

Number of frequency steps for the stepped form of Price's NLFM, specified as a positive integer.

Example: 10

Dependencies

To enable this property, set the FrequencyModulation property to 'Stepped Price'.

Data Types: double

BandwidthFactors — Bandwidth factors

[1e4 2e4] (default) | 2-element positive-valued vector

Bandwidth factors for the stepped form of Price's NLFM, specified as a two-element positive-valued vector of the form [BL BC]. BL determines the bandwidth of the linear component of the waveform and BC determines the bandwidth of the nonlinear component. The total sweep bandwidth is equal to (M-1)/M*(BL+BC*M/sqrt(2*M-1)), where M is the value of the NumSteps property. As M, increases the bandwidth of the linear component approximately equals BL, while the bandwidth of the nonlinear component grows with M.

Dependencies

To enable this property, set the FrequencyModulation property to 'Stepped Price'.

Data Types: double

HyperbolicStartFrequency — Start frequency of hyperbolic FM waveform

200e3 (default) | positive scalar

Start frequency of the hyperbolic frequency modulated waveform, specified as a positive scalar. Units are in Hz.

Dependencies

To enable this property, set the FrequencyModulation property to 'Hyperbolic'.

Data Types: double

SweepBandwidth — Bandwidth of nonlinear FM sweep

100e3 (default) | positive scalar

Bandwidth of nonlinear FM sweep, specified as a positive scalar. Units are in Hz.

Data Types: double

SweepDirection — Direction of nonlinear FM sweep

'Up' (default) | 'Down'

Direction of the nonlinear FM sweep, specified as 'Up' or 'Down'.

Data Types: char | string

SweepInterval — Location of FM sweep interval

'Positive' (default) | 'Symmetric'

Location of the FM sweep interval, specified as'Positive' or 'Symmetric'.

• If SweepInterval is 'Positive', the waveform sweeps the interval between 0 and B where B is the sweep bandwidth in the SweepBandwidth property.

• If SweepInterval is 'Symmetric', the waveform sweeps the interval between -B/2 and B/2.

Data Types: char | string

Envelope — Waveform envelope function

'Rectangular' (default) | 'Gaussian' | 'Hamming' | 'Chebyshev' | 'Hann' | 'Kaiser' | 'Taylor' | 'Custom'

Waveform envelope function, specified as 'Rectangular', 'Gaussian', 'Hamming', 'Chebyshev', 'Hann', 'Kaiser', 'Taylor', or 'Custom'.

When Envelope is set to 'Custom' use the CustomEnvelope property to specify a custom envelope.

Example: 'Taylor'

Data Types: char | string

EnvelopeSidelobeLevel — Envelope window sidelobe level

30 (default) | positive scalar

Sidelobe level of a Kaiser, Chebyshev, or Taylor window used as the waveform envelope, specified as a positive scalar. Units are in dB.

Dependencies

To enable this property, set the Envelope property to 'Kaiser', 'Chebyshev', or 'Taylor'.

Data Types: double

CustomEnvelope — User-defined waveform envelope

@gausswin (default) | function handle | cell array

User-defined waveform envelope, specified as a function handle or cell array.

• If CustomEnvelope is a function handle, the specified function uses the window length as input and generates appropriate window coefficients.

• If CustomEnvelope is a cell array, then the first cell must be a function handle. The specified function takes the window length as the first input argument, with other additional input arguments if necessary, and generates appropriate window coefficients. The remaining entries in the cell array serve as additional input arguments to the function.

Example: {@chebwin,512,100}

Dependencies

To enable this property, set the Envelope property to 'Custom'.

Data Types: cell | function_handle

FrequencyOffsetSource — Source of frequency offset

'Property' (default) | 'Input port'

Source of frequency offset, specified as 'Property' or 'Input port'.

• When you set this property to 'Property', the frequency offset is determined by the value of the FrequencyOffset property.

• When you set this property to 'Input port', the frequency offset is determined by the input argument freqoffset when calling the object.

Example: 'Input port'

Data Types: char | string

FrequencyOffset — Frequency offset

0 (default) | scalar

Frequency offset, specified as a scalar. Units are in Hz.

Example: 150.0

Dependencies

To enable this property, set the FrequencyOffsetSource property to 'Property'.

Data Types: double

OutputFormat — Format of output signal

'Pulses' (default) | 'Samples'

Format of output signal, specified as 'Pulses' or 'Samples'.

• When you set the OutputFormat property to 'Pulses', the output of the object takes the form of multiple pulses specified by the value of the NumPulses property. The number of samples per pulse can vary if you change the PRF during the simulation.

• When you set the OutputFormat property to 'Samples', the output of the object takes the form of multiple samples. In this case, the number of output signal samples is the value of the NumSamples property and is fixed.

Data Types: char | string

NumSamples — Number of samples in output

100 (default) | positive integer

Number of samples in each output of the object, specified as a positive integer.

Dependencies

To enable this property, set the OutputFormat property to 'Samples'.

Data Types: double

NumPulses — Number of pulses in output

1 (default) | positive integer

Number of pulses in each output, specified as a positive integer.

Dependencies

To enable this property, set the OutputFormat property to 'Pulses'.

Data Types: double

PRFOutputPort — Enable PRF output

false (default) | true

Enable PRF output, specified as false or true. Set this property to true to output the PRF.

Dependencies

To enable this property, set the OutputFormat property to 'Pulses'.

Data Types: logical

CoefficientsOutputPort — Enable matched filter coefficients output

false (default) | true

Enable matched filter coefficients output, specified as false or true. Set this property to true to enable the object the output of the matched filter coefficients of the waveform used during the simulation.

Data Types: logical

Usage

Syntax

Y = waveform()

Y = waveform(prfidx)

Y = waveform(freqoffset)

[Y,PRF] = waveform(___)

[Y,coeff]= waveform()

Description

Y = waveform() returns samples of the nonlinear FM pulse in a column vector Y. Y can contain either a certain number of pulses or a certain number of samples.

Y = waveform(prfidx) specifies the index of the pulse repetition frequency (PRF), prfidx. The index identifies the entries specified in the PRF property. This syntax applies when you set the PRFSelectionInputPort property to true.

Use this syntax for the cases where the transmitted pulse needs to be dynamically selected. In such situations, the PRF property includes a list of predetermined choices of PRF's. During the simulation, using prfidx, one of the PRFs is selected as the PRF for the next transmission.

Note that the transmission always finishes the current pulse before starting the next pulse. Therefore, when you set the OutputFormat property to 'Samples' and then specify the NumSamples property to be shorter than a pulse, it is possible that during a given simulation step, if the entire output is needed to finish the previously transmitted pulse, the specified prfidx is ignored.

Y = waveform(freqoffset) specifies the value of the frequency offset freqoffset as a finite real value. The offset is used to generate the waveform with a frequency offset. Use this syntax for the cases where the transmit pulse frequency needs to be dynamically updated. To enable this syntax set the FrequencyOffsetSource property to 'Input port'.

[Y,PRF] = waveform(___) also returns the current pulse repetition frequency, PRF. To enable this syntax, set the PRFOutputPort property to true and set the OutputFormat property to 'Pulses'.

[Y,coeff]= waveform() returns an additional output coeff, as the matched filter coefficients. To use this syntax, set the CoefficientsOutputPort property to true.

You can combine optional input and output arguments when their enabling properties are set. Optional inputs and outputs must be listed in the same order as the order of the enabling properties. For example,

[Y,PRF,coeff] = waveform(prfidx,freqoffset)

Input Arguments

prfidx — index of pulse repetition frequency

positive integer

Index of pulse repetition frequency, specified as a positive integer. The index identifies the entries in the PRF property. This syntax applies when you set the PRFSelectionInputPort property to true. Use this argument for the case when the transmit pulse needs to be dynamically selected. Under such situations, the PRF property includes a list of predetermined choices of PRFs. During the simulation, based on the PRF index input, one of the PRFs is selected as the PRF for the next transmission.

freqoffset — frequency offset

0 (default) | scalar

Frequency offset, specified as a scalar. This argument generates the waveform with a frequency offset when the object is called. Use this syntax for the cases where the transmit pulse frequency needs to be dynamically updated.

Dependencies

To use this argument, set the FrequencyOffsetSource property to 'Input port'.

Data Types: double

Output Arguments

PRF — pulse repetition frequency

scalar

Pulse repetition frequency, returned as a scalar. Returns the current PRF used by the object. Units are in Hz.

Dependencies

To enable this argument, set the PRFOutputPort property to true and set the OutputFormat to 'Pulses'.

coeff — matched filter coefficients

N_Z-by-1 complex-valued vector | N_Z-by-M complex-valued matrix

Matched filter coefficients, returned as an N_Z-by-1 complex-valued vector or an N_Z-by-M complex-valued matrix.

• If you set OutputFormat to 'Pulses' and NumPulses is 1, the object returns coeff as an N_Z-length vector. N_Z corresponds to the pulse width.

• If you set OutputFormat to 'Pulses' with NumPulses greater than 1 or OutputFormat is 'Samples' and DurationSpecification is 'Pulse width', coeff is returned as an N_Z-length vector. N_Z corresponds to the pulse width.

• If OutputFormat is set to 'Pulses' with NumPulses greater than 1 or OutputFormat is set to 'Samples' and DurationSpecification is set to 'Duty cycle' with only one unique PRF value, coeff is returned as an N_Z-length vector. N_Z corresponds to the pulse width.

• If OutputFormat is 'Pulses' with NumPulses greater than 1 or OutputFormat is 'Samples' and DurationSpecification is 'Duty cycle', coeff is returned as an N_Z-by-M matrix. N_Z corresponds to the maximum pulse width and M corresponds to the number of unique PRFs.

Dependencies

To enable this argument, set the CoefficientsOutputPort property to true.

Data Types: double
Complex Number Support: Yes

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Specific to waveform System objects

bandwidth	Waveform bandwidth
getMatchedFilter	Matched filter coefficients derived from waveform
plot	Plot pulse waveform

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

Create Nonlinear FM Waveform with Default Properties

Create a nonlinear FM waveform with the default polynomial frequency modulation.

waveform = phased.NonlinearFMWaveform() 

waveform = 
  phased.NonlinearFMWaveform with properties:

                SampleRate: 1000000
     DurationSpecification: 'Pulse width'
                PulseWidth: 5.0000e-05
                       PRF: 10000
     PRFSelectionInputPort: false
       FrequencyModulation: 'Polynomial'
    PolynomialCoefficients: [1 0 0]
            SweepBandwidth: 100000
             SweepInterval: 'Positive'
                  Envelope: 'Rectangular'
     FrequencyOffsetSource: 'Property'
           FrequencyOffset: 0
              OutputFormat: 'Pulses'
                 NumPulses: 1
             PRFOutputPort: false
    CoefficientsOutputPort: false

Display the real part of the waveform.

plot(waveform)

Plot Quadratic FM Pulse Waveform

Create and plot a quadratic FM pulse waveform. The pulse has a 10 MHz bandwidth and 50 $\mu$sec duration. The pulse sample rate is 10 times the bandwidth.

BW = 10e6;
T = 50e-6;
waveform = phased.NonlinearFMWaveform( ...
    'SampleRate',10*BW,'SweepBandwidth',BW, ...
    'PulseWidth',T);
plot(waveform,PlotType='complex')

Create Hybrid Linear-Tangent FM Waveform

Generate samples of a hybrid linear-tangent FM waveform with a bandwidth of 2 kHz and a pulse width of 100 ms. Set the pulse repetition frequency to 5 Hz and the sample frequency to 20 kHz. Set the factor controlling the balance between the linear and the nonlinear terms to 0.5. Set the factor controlling the portion of the tan(x) curve used for frequency modulation to 1.4. Plot the autocorrelation function to determine the resulting range sidelobe level.

BW = 2000;
T = 100e-3;
PRF = 5;
fs = 10*BW;

Set the balance between tan-FM and LFM to 0.5 and set the portion of tan(x) to use to 1.4.

alpha = 0.5;
gamma = 1.4;

Create the waveform and plot the real and imaginary parts.

waveform = phased.NonlinearFMWaveform('SampleRate',fs,'PulseWidth',T, ...
    'PRF',PRF,'FrequencyModulation','Hybrid Linear-Tangent', ...
    'LinearTangentBalance',alpha,'TangentCurvePortion',gamma, ...
    'SweepBandwidth',BW,'OutputFormat','Pulses','NumPulses',2);
wav = waveform();
figure
plot(waveform,PlotType='complex')

Compute and plot the autocorrelation function.

[acf,delay] = ambgfun(wav,waveform.SampleRate,waveform.PRF, ...
    Cut='Doppler');
figure
plot(delay/waveform.PulseWidth,mag2db(acf),LineWidth=2)
grid on
xlim([-0.25 0.25])
ylim([-60 1])
xlabel('Delay (\tau/T)')
ylabel('Autocorrelation (dB)')

Plot Stepped Version of Price's Waveform

Generate output samples of a nonlinear FM pulse waveform based on the stepped version of Price's waveform. The pulse width is 5e-6 seconds. The waveform performs 50 frequency steps within one pulse. The time-bandwidth products of the linear and nonlinear components are 20 and 40 respectively. The start frequency of the sweep is 15 MHz. Generate matched filter coefficients and then apply the matched filter.

T = 5e-6;
M = 50;
BLT = 20;
BCT = 40;
bfs = [BLT BCT]/T;
fs = 100e6;
fstart = 15e6;

waveform = phased.NonlinearFMWaveform(SampleRate=fs, ...
    PulseWidth=T,FrequencyModulation='Stepped Price', ...
    BandwidthFactors=bfs,NumSteps=M,FrequencyOffset=fstart, ...
    OutputFormat='Pulses',CoefficientsOutputPort=true);

Plot the complex waveform.

figure
plot(waveform,PlotType='complex')

Obtain the resulting sweep bandwidth (Hz)

bandwidth(waveform)

ans = 
4.3317e+07

Find the matched filter coefficients. Then plot the filtered waveform.

[wav,coeff] = waveform();
mf = phased.MatchedFilter(CoefficientsSource='Input port');
mfout = mf(wav,coeff);

Plot the filter input and output.

figure
subplot(211)
plot(real(wav))
grid on
xlabel('Samples')
ylabel('Amplitude (V)')
title('Input Signal')

subplot(212)
plot(abs(mfout));
grid on
xlabel('Samples')
ylabel('Amplitude (V)')
title('Matched Filter Output')

Plot Spectrogram of Hyperbolic FM Waveform

Create a hyperbolic frequency modulated (HFM) waveform. The start and the stop frequencies of the sweep are 100 kHz and 20 kHz, respectively. The pulse width is 50 ms. The sample rate is 200 kHz. Plot the spectrogram.

f1 = 100e3;
f2 = 20e3;
BW = f1 - f2;
T = 50e-3;
fs = 2*f1;

Create a hyperbolic FM waveform.

waveform = phased.NonlinearFMWaveform( ...
    SampleRate=fs,PulseWidth=T,SweepBandwidth=BW, ...
    FrequencyModulation='Hyperbolic', ...
    HyperbolicStartFrequency=f1, ...
    SweepDirection='down',PRF=1/T);
sig = waveform();
spectrogram(sig, 256, 128, 1024, fs, 'yaxis')

References

[1] Collins, T., and P. Atkins. "Nonlinear frequency modulation chirps for active sonar." IEE Proceedings-Radar, Sonar and Navigation 146.6 (1999): 312-316.

[2] Levanon, Nadav, and Eli Mozeson. Radar signals. John Wiley & Sons, 2004, pp. 92-93.

[3] Doerry, Armin Walter. "Generating nonlinear FM chirp waveforms for radar". No. SAND2006-5856. Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA (United States), 2006.

[4] Cook, C. E. "A class of nonlinear FM pulse compression signals." Proceedings of the IEEE 52.11 (1964): 1369-1371.

[5] Yang, J., and T. K. Sarkar. "Doppler‐invariant property of hyperbolic frequency modulated waveforms." Microwave and optical technology letters 48.6 (2006): 1174-1179.

[6] Melvin, William L., and James Scheer. Principles of modern radar: advanced techniques. SciTech Pub., 2013.

[7] Alphonse, Sebastian, and Geoffrey A. Williamson. "Evaluation of a class of NLFM radar signals." EURASIP Journal on Advances in Signal Processing 2019.1 (2019): 1-12.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2023a