assempde
(Not recommended) Assemble finite element matrices and solve elliptic PDE
assempde is not recommended. Use solvepde instead.
Syntax
Description
[,
for any of the previous input syntaxes, assembles finite element matrices using
the reduced linear system form, which eliminates any
Dirichlet boundary conditions from the system of linear equations. You can
calculate the solution Kc,Fc,B,ud]
= assempde(___)u at node points by the command
u = B*(Kc\Fc) + ud. See Reduced Linear System.
[
assembles finite element matrices that represent any Dirichlet boundary
conditions using a stiff-spring approximation. You can
calculate the solution Ks,Fs]
= assempde(___)u at node points by the command
u = Ks\Fs. See Stiff-Spring Approximation.
Examples
Solve an elliptic PDE on an L-shaped region.
Create a scalar PDE model. Incorporate the geometry of an L-shaped region.
model = createpde; geometryFromEdges(model,@lshapeg);
Apply zero Dirichlet boundary conditions to all edges.
applyBoundaryCondition(model,Edge=1:model.Geometry.NumEdges, ...
u=0,InternalBC=true);Generate a finite element mesh.
generateMesh(model,GeometricOrder="linear");Solve the PDE with parameters c = 1, a = 0, and f = 5.
c = 1; a = 0; f = 5; u = assempde(model,c,a,f);
Plot the solution.
pdeplot(model,XYData=u)
axis equal
Solve a 3-D elliptic PDE using a PDE model.
Create a PDE model container, import a 3-D geometry description, and view the geometry.
model = createpde; importGeometry(model,'Block.stl'); pdegplot(model,FaceAlpha=0.5, ... FaceLabels="on")
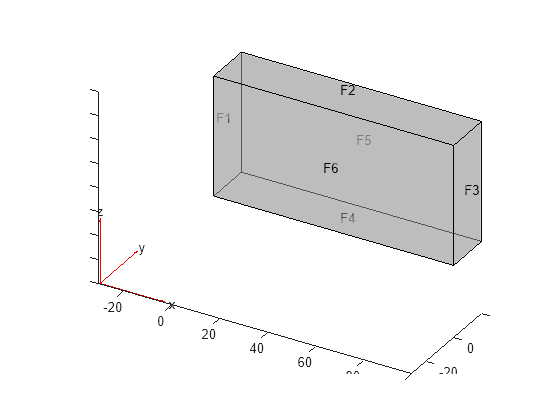
Set zero Dirichlet conditions on faces 1 through 4 (the edges). Set Neumann conditions with g = -1 on face 6 and g = 1 on face 5.
applyBoundaryCondition(model,Face=1:4, ... u=0); applyBoundaryCondition(model,Face=6, ... g=-1); applyBoundaryCondition(model,Face=5, ... g=1);
Set coefficients c = 1, a = 0, and f = 0.1.
c = 1; a = 0; f = 0.1;
Create a mesh and solve the problem.
msh = generateMesh(model); u = assempde(model,c,a,f);
Plot the solution on the surface.
pdeplot3D(msh,ColorMapData=u)

Solve a 2-D PDE using the older syntax for mesh.
Create a circle geometry.
g = @circleg;
Set zero Dirichlet boundary conditions.
b = @circleb1;
Create a mesh for the geometry.
[p,e,t] = initmesh(g);
Solve the PDE with parameters c = 1, a = 0, and f = sin(x).
c = 1;
a = 0;
f = 'sin(x)';
u = assempde(b,p,e,t,c,a,f);Plot the solution.
pdeplot(p,e,t,XYData=u)
axis equal
Obtain the finite-element matrices that represent the problem using a reduced linear algebra representation of Dirichlet boundary conditions.
Create a scalar PDE model. Import a simple 3-D geometry.
model = createpde;
importGeometry(model,"Block.stl");Set zero Dirichlet boundary conditions on all the geometry faces.
applyBoundaryCondition(model,"dirichlet", ... Face=1:model.Geometry.NumFaces, ... u=0);
Generate a mesh for the geometry.
generateMesh(model);
Obtain finite element matrices K, F, B, and ud that represent the equation with parameters , , and .
c = 1;
a = 0;
f = 'log(1+x+y./(1+z))';
[K,F,B,ud] = assempde(model,c,a,f);You can obtain the solution u of the PDE at mesh nodes by executing the command
u = B*(K\F) + ud;
Generally, this solution is slightly more accurate than the stiff-spring solution, as calculated in the next example.
Obtain the stiff-spring approximation of finite element matrices.
Create a scalar PDE model. Import a simple 3-D geometry.
model = createpde;
importGeometry(model,"Block.stl");Set zero Dirichlet boundary conditions on all the geometry faces.
applyBoundaryCondition(model,Face=1:model.Geometry.NumFaces,u=0);
Generate a mesh for the geometry.
generateMesh(model);
Obtain finite element matrices Ks and Fs that represent the equation with parameters , , and .
c = 1;
a = 0;
f = "log(1+x+y./(1+z))";
[Ks,Fs] = assempde(model,c,a,f);You can obtain the solution u of the PDE at mesh nodes by executing the command
u = Ks\Fs;
Generally, this solution is slightly less accurate than the reduced linear algebra solution, as calculated in the previous example.
Obtain the full collection of finite element matrices for an elliptic problem.
Import geometry and set up an elliptic problem with Dirichlet boundary conditions. The Torus.stl geometry has only one face, so you need set only one boundary condition.
model = createpde();
importGeometry(model,"Torus.stl");
applyBoundaryCondition(model,Face=1,u=0);
c = 1;
a = 0;
f = 1;
generateMesh(model);Create the finite element matrices that represent this problem.
[K,M,F,Q,G,H,R] = ...
assempde(model,c,a,f);Most of the resulting matrices are quite sparse. G, M, Q, and R are all zero sparse matrices.
howsparse = @(x)nnz(x)/numel(x); disp(['Maximum fraction of nonzero' ... ' entries in K or H is ',... num2str(max(howsparse(K),howsparse(H)))])
Maximum fraction of nonzero entries in K or H is 0.0019281
To find the solution to the PDE, call assempde again.
u = assempde(K,M,F,Q,G,H,R);
Input Arguments
PDE model, specified as a PDEModel object.
Example: model = createpde
PDE coefficient, specified as a scalar, matrix, character vector, character array, string
scalar, string vector, or coefficient function. c
represents the c coefficient in the scalar PDE
or in the system of PDEs
Example: 'cosh(x+y.^2)'
Data Types: double | char | string | function_handle
Complex Number Support: Yes
PDE coefficient, specified as a scalar, matrix, character vector, character array, string
scalar, string vector, or coefficient function. a represents the
a coefficient in the scalar PDE
or in the system of PDEs
Example: 2*eye(3)
Data Types: double | char | string | function_handle
Complex Number Support: Yes
PDE coefficient, specified as a scalar, matrix, character vector, character array, string
scalar, string vector, or coefficient function. f
represents the f coefficient in the scalar PDE
or in the system of PDEs
Example: char('sin(x)';'cos(y)';'tan(z)')
Data Types: double | char | string | function_handle
Complex Number Support: Yes
Boundary conditions, specified as a boundary matrix or boundary file. Pass a boundary file as a function handle or as a file name. A boundary matrix is generally an export from the PDE Modeler app.
Example: b = 'circleb1', b = "circleb1", or b =
@circleb1
Data Types: double | char | string | function_handle
Mesh points, specified as a 2-by-Np matrix of points, where
Np is the number of points in the mesh. For a description of the
(p,e,t) matrices, see Mesh Data as [p,e,t] Triples.
Typically, you use the p, e, and t
data exported from the PDE Modeler app, or generated by initmesh or refinemesh.
Example: [p,e,t] = initmesh(gd)
Data Types: double
Mesh edges, specified as a 7-by-Ne matrix of edges,
where Ne is the number of edges in the mesh. For a description of the
(p,e,t) matrices, see Mesh Data as [p,e,t] Triples.
Typically, you use the p, e, and t
data exported from the PDE Modeler app, or generated by initmesh or refinemesh.
Example: [p,e,t] = initmesh(gd)
Data Types: double
Mesh triangles, specified as a 4-by-Nt matrix of
triangles, where Nt is the number of triangles in the mesh. For a
description of the (p,e,t)
matrices, see Mesh Data as [p,e,t] Triples.
Typically, you use the p, e, and t
data exported from the PDE Modeler app, or generated by initmesh or refinemesh.
Example: [p,e,t] = initmesh(gd)
Data Types: double
Stiffness matrix, specified as a sparse matrix or full matrix. Generally,
you obtain K from a previous call to assema or
assempde. For the meaning of stiffness matrix, see
Elliptic Equations.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Mass matrix, specified as a sparse matrix or full matrix. Generally, you
obtain M from a previous call to assema or
assempde. For the meaning of mass matrix, see Elliptic Equations.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Finite element f representation, specified as a vector.
Generally, you obtain F from a previous call to assema or
assempde. For the meaning of this representation,
see Elliptic Equations.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Neumann boundary condition matrix, specified as a sparse matrix or full
matrix. Generally, you obtain Q from a previous call to
assemb or
assempde. For the meaning of this matrix, see Elliptic Equations.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Neumann boundary condition vector, specified as a sparse vector or full
vector. Generally, you obtain G from a previous call to
assemb or
assempde. For the meaning of this vector, see Elliptic Equations.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Dirichlet boundary condition matrix, specified as a sparse matrix or full
matrix. Generally, you obtain H from a previous call to
assemb or
assempde. For the meaning of this matrix, see Algorithms.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Dirichlet boundary condition vector, specified as a sparse vector or full
vector. Generally, you obtain R from a previous call to
assemb or
assempde. For the meaning of this vector, see Algorithms.
Example: [K,M,F,Q,G,H,R] =
assempde(model,c,a,f)
Data Types: double
Complex Number Support: Yes
Subdomain labels, specified as a vector of positive integers. For 2-D geometry only. View the subdomain labels in your geometry using the command
pdegplot(g,'SubdomainLabels','on')
Example: sdl = [1,3:5];
Data Types: double
Output Arguments
PDE solution, returned as a vector.
If the PDE is scalar, meaning only one equation, then
uis a column vector representing the solution u at each node in the mesh.u(i)is the solution at theith column ofmodel.Mesh.Nodesor theith column ofp.If the PDE is a system of N > 1 equations, then
uis a column vector with N*Npelements, whereNpis the number of nodes in the mesh. The firstNpelements ofurepresent the solution of equation 1, then nextNpelements represent the solution of equation 2, etc.
To obtain the solution at an arbitrary point in the geometry,
use pdeInterpolant.
Stiffness matrix, returned as a sparse matrix. See Elliptic Equations.
u1 = Kc\Fc returns the solution on the non-Dirichlet
points. To obtain the solution u at the nodes of the
mesh,
u = B*(Kc\Fc) + ud
Generally, Kc, Fc,
B, and ud make a slower but more
accurate solution than Ks and
Fs.
Load vector, returned as a vector. See Elliptic Equations.
u = B*(Kc\Fc) + ud
Generally, Kc, Fc,
B, and ud make a slower but more
accurate solution than Ks and
Fs.
Dirichlet nullspace, returned as a sparse matrix. See Algorithms.
u = B*(Kc\Fc) + ud
Generally, Kc, Fc,
B, and ud make a slower but more
accurate solution than Ks and
Fs.
Dirichlet vector, returned as a vector. See Algorithms.
u = B*(Kc\Fc) + ud
Generally, Kc, Fc,
B, and ud make a slower but more
accurate solution than Ks and
Fs.
Finite element matrix for stiff-spring approximation, returned as a sparse matrix. See Algorithms.
To obtain the solution u at the nodes of the
mesh,
u = Ks\Fs.
Generally, Ks and Fs make a quicker
but less accurate solution than Kc,
Fc, B, and
ud.
Load vector corresponding to the stiff-spring approximation for Dirichlet boundary condition, returned as a vector. See Algorithms.
To obtain the solution u at the nodes of the
mesh,
u = Ks\Fs.
Generally, Ks and Fs make a quicker
but less accurate solution than Kc,
Fc, B, and
ud.
Stiffness matrix, returned as a sparse matrix. See Elliptic Equations.
K represents the stiffness matrix alone, unlike
Kc or Ks, which are stiffness
matrices combined with other terms to enable immediate solution of a
PDE.
Typically, you use K in a subsequent call to a solver
such as assempde or
hyperbolic.
Mass matrix. returned as a sparse matrix. See Elliptic Equations.
Typically, you use M in a subsequent call
to a solver such as assempde or hyperbolic.
Load vector, returned as a vector. See Elliptic Equations.
F represents the load vector alone, unlike Fc or Fs, which are load vectors
combined with other terms to enable immediate solution of a PDE.
Typically, you use F in a subsequent call to a solver
such as assempde or
hyperbolic.
Neumann boundary condition matrix, returned as a sparse matrix. See Elliptic Equations.
Typically, you use Q in a subsequent call
to a solver such as assempde or hyperbolic.
Neumann boundary condition vector, returned as a sparse vector. See Elliptic Equations.
Typically, you use G in a subsequent call
to a solver such as assempde or hyperbolic.
Dirichlet matrix, returned as a sparse matrix. See Algorithms.
Typically, you use H in a subsequent call to a solver
such as assempde or
hyperbolic.
Dirichlet vector, returned as a sparse vector. See Algorithms.
Typically, you use R in a subsequent call to a solver
such as assempde or
hyperbolic.
More About
This form of the finite element matrices eliminates Dirichlet
conditions from the problem using a linear algebra approach. The finite element
matrices reduce to the solution u = B*(Kc\Fc) + ud, where
B spans the null space of the columns of
H (the Dirichlet condition matrix representing
hu = r). R is the
Dirichlet condition vector for Hu = R. ud
is the vector of boundary condition solutions for the Dirichlet conditions.
u1 = Kc\Fc returns the
solution on the non-Dirichlet points.
See Systems of PDEs for details on the approach used to eliminate Dirichlet conditions.
This form of the finite element matrices converts Dirichlet
boundary conditions to Neumann boundary conditions using a stiff-spring
approximation. Using this approximation, assempde returns a
matrix Ks and a vector Fs that represent
the combined finite element matrices. The approximate solution
u is u = Ks\Fs.
See Elliptic Equations. For details of the stiff-spring approximation, see Systems of PDEs.
Algorithms
Partial Differential Equation Toolbox™ solves equations of the form
When the m and d coefficients are 0, this reduces to
which the documentation calls an elliptic equation, whether or not the equation is elliptic in the mathematical sense. The equation holds in Ω, where Ω is a bounded domain in two or three dimensions. c, a, f, and the unknown solution u are complex functions defined on Ω. c can also be a 2-by-2 matrix function on Ω. The boundary conditions specify a combination of u and its normal derivative on the boundary:
Dirichlet: hu = r on the boundary ∂Ω.
Generalized Neumann: · (c∇u) + qu = g on ∂Ω.
Mixed: Only applicable to systems. A combination of Dirichlet and generalized Neumann.
is the outward unit normal. g, q, h, and r are functions defined on ∂Ω.
Our nomenclature deviates slightly from the tradition for potential theory, where a Neumann condition usually refers to the case q = 0 and our Neumann would be called a mixed condition. In some contexts, the generalized Neumann boundary conditions is also referred to as the Robin boundary conditions. In variational calculus, Dirichlet conditions are also called essential boundary conditions and restrict the trial space. Neumann conditions are also called natural conditions and arise as necessary conditions for a solution. The variational form of the Partial Differential Equation Toolbox equation with Neumann conditions is given below.
The approximate solution to the elliptic PDE is found in three steps:
Describe the geometry of the domain Ω and the boundary conditions. For 2-D geometry, create geometry using the PDE Modeler app or through MATLAB® files. For 3-D geometry, import the geometry in STL file format.
Build a triangular mesh on the domain Ω. The software has mesh generating and mesh refining facilities. A mesh is described by three matrices of fixed format that contain information about the mesh points, the boundary segments, and the elements.
Discretize the PDE and the boundary conditions to obtain a linear system Ku = F. The unknown vector u contains the values of the approximate solution at the mesh points, the matrix K is assembled from the coefficients c, a, h, and q and the right-hand side F contains, essentially, averages of f around each mesh point and contributions from g. Once the matrices K and F are assembled, you have the entire MATLAB environment at your disposal to solve the linear system and further process the solution.
More elaborate applications make use of the Finite Element Method (FEM) specific information returned by the different functions of the software. Therefore we quickly summarize the theory and technique of FEM solvers to enable advanced applications to make full use of the computed quantities.
FEM can be summarized in the following sentence: Project the weak form of the differential equation onto a finite-dimensional function space. The rest of this section deals with explaining the preceding statement.
We start with the weak form of the differential equation. Without restricting the generality, we assume generalized Neumann conditions on the whole boundary, since Dirichlet conditions can be approximated by generalized Neumann conditions. In the simple case of a unit matrix h, setting g = qr and then letting q → ∞ yields the Dirichlet condition because division with a very large q cancels the normal derivative terms. The actual implementation is different, since the preceding procedure may create conditioning problems. The mixed boundary condition of the system case requires a more complicated treatment, described in Systems of PDEs.
Assume that u is a solution of the differential equation. Multiply the equation with an arbitrary test function v and integrate on Ω:
Integrate by parts (i.e., use Green's formula) to obtain
The boundary integral can be replaced by the boundary condition:
Replace the original problem with Find u such that
This equation is called the variational, or weak, form of the differential equation. Obviously, any solution of the differential equation is also a solution of the variational problem. The reverse is true under some restrictions on the domain and on the coefficient functions. The solution of the variational problem is also called the weak solution of the differential equation.
The solution u and the test functions v belong to some function space V. The next step is to choose an Np-dimensional subspace . Project the weak form of the differential equation onto a finite-dimensional function space simply means requesting u and v to lie in rather than V. The solution of the finite dimensional problem turns out to be the element of that lies closest to the weak solution when measured in the energy norm. Convergence is guaranteed if the space tends to V as Np→∞. Since the differential operator is linear, we demand that the variational equation is satisfied for Np test-functions Φi ∊ that form a basis, i.e.,
Expand u in the same basis of elements
and obtain the system of equations
Use the following notations:
and rewrite the system in the form
| (K + M + Q)U = F + G. | (1) |
K, M, and Q are
Np-by-Np
matrices, and F and G are
Np-vectors. K,
M, and F are produced by
assema, while Q, G are
produced by assemb. When it is not necessary to distinguish
K, M, and Q or
F and G, we collapse the notations to
KU = F, which form the output of
assempde.
When the problem is self-adjoint and elliptic in the usual mathematical sense, the matrix K + M + Q becomes symmetric and positive definite. Many common problems have these characteristics, most notably those that can also be formulated as minimization problems. For the case of a scalar equation, K, M, and Q are obviously symmetric. If c(x) ≥ δ > 0, a(x) ≥ 0 and q(x) ≥ 0 with q(x) > 0 on some part of ∂Ω, then, if U ≠ 0.
UT(K + M + Q)U is the energy norm. There are many choices of the test-function spaces. The software uses continuous functions that are linear on each element of a 2-D mesh, and are linear or quadratic on elements of a 3-D mesh. Piecewise linearity guarantees that the integrals defining the stiffness matrix K exist. Projection onto is nothing more than linear interpolation, and the evaluation of the solution inside an element is done just in terms of the nodal values. If the mesh is uniformly refined, approximates the set of smooth functions on Ω.
A suitable basis for in 2-D is the set of “tent” or “hat” functions ϕi. These are linear on each element and take the value 0 at all nodes xj except for xi. For the definition of basis functions for 3-D geometry, see Finite Element Basis for 3-D. Requesting ϕi(xi) = 1 yields the very pleasant property
That is, by solving the FEM system we obtain the nodal values of the approximate solution. The basis function ϕi vanishes on all the elements that do not contain the node xi. The immediate consequence is that the integrals appearing in Ki,j, Mi,j, Qi,j, Fi and Gi only need to be computed on the elements that contain the node xi. Secondly, it means that Ki,j andMi,j are zero unless xi and xj are vertices of the same element and thus K and M are very sparse matrices. Their sparse structure depends on the ordering of the indices of the mesh points.
The integrals in the FEM matrices are computed by adding the contributions from each
element to the corresponding entries (i.e., only if the corresponding mesh point is a vertex
of the element). This process is commonly called assembling, hence the
name of the function assempde.
The assembling routines scan the elements of the mesh. For each element they compute the so-called local matrices and add their components to the correct positions in the sparse matrices or vectors.
The discussion now specializes to triangular meshes in 2-D. The local 3-by-3 matrices contain the integrals evaluated only on the current triangle. The coefficients are assumed constant on the triangle and they are evaluated only in the triangle barycenter. The integrals are computed using the midpoint rule. This approximation is optimal since it has the same order of accuracy as the piecewise linear interpolation.
Consider a triangle given by the nodes P1, P2, and P3 as in the following figure.

Note
The local 3-by-3 matrices contain the integrals evaluated only on the current triangle. The coefficients are assumed constant on the triangle and they are evaluated only in the triangle barycenter.
The simplest computations are for the local mass matrix m:
where Pc is the center of mass of Δ P1P2P3, i.e.,
The contribution to the right side F is just
For the local stiffness matrix we have to evaluate the gradients of the basis functions that do not vanish on P1P2P3. Since the basis functions are linear on the triangle P1P2P3, the gradients are constants. Denote the basis functions ϕ1, ϕ2, and ϕ3 such that ϕ(Pi) = 1. If P2 – P3 = [x1,y1]T then we have that
and after integration (taking c as a constant matrix on the triangle)
If two vertices of the triangle lie on the boundary ∂Ω, they contribute to the line integrals associated to the boundary conditions. If the two boundary points are P1 and P2, then we have
and
where Pb is the midpoint of P1P2.
For each triangle the vertices Pm of the local triangle correspond to the indices im of the mesh points. The contributions of the individual triangle are added to the matrices such that, e.g.,
This is done by the function assempde. The gradients and the areas of
the triangles are computed by the function pdetrg.
The Dirichlet boundary conditions are treated in a slightly different manner. They are
eliminated from the linear system by a procedure that yields a symmetric, reduced system.
The function assempde can return matrices K,
F, B, and ud such that the
solution is u = Bv + ud where Kv = F. u is an
Np-vector, and if the rank of the Dirichlet
conditions is rD, then v has
Np – rD
components.
To summarize, assempde performs the following steps to obtain a
solution u to an elliptic PDE:
Generate the finite element matrices [
K,M,F,Q,G,H,R]. This step is equivalent to callingassemato generate the matricesK,M, andF, and also callingassembto generate the matricesQ,G,H, andR.Generate the combined finite element matrices [
Kc,Fc,B,ud]. The combined stiffness matrix is for the reduced linear system,Kc = K + M + Q. The corresponding combined load vector isFc = F + G. TheBmatrix spans the null space of the columns ofH(the Dirichlet condition matrix representing hu = r). TheRvector represents the Dirichlet conditions inHu = R. Theudvector represents boundary condition solutions for the Dirichlet conditions.Calculate the solution
uviau = B*(Kc\Fc) + ud.
assempde uses one of two algorithms for assembling a problem into
combined finite element matrix form. A reduced linear system form
leads to immediate solution via linear algebra. You choose the algorithm by the number of
outputs. For the reduced linear system form, request four outputs:
[Kc,Fc,B,ud] = assempde(_)
For the stiff-spring approximation, request two outputs:
[Ks,Fs] = assempde(_)
For details, see Reduced Linear System and Stiff-Spring Approximation.
Partial Differential Equation Toolbox software can also handle systems of N partial differential equations over the domain Ω. We have the elliptic system
the parabolic system
the hyperbolic system
and the eigenvalue system
where c is an N-by-N-by-D-by-D tensor, and D is the geometry dimensions, 2 or 3.
For 2-D systems, the notation represents an N-by-1 matrix with an (i,1)-component
For 3-D systems, the notation represents an N-by-1 matrix with an (i,1)-component
The symbols a and d denote N-by-N matrices, and f denotes a column vector of length N.
The elements cijkl,
aij,
dij, and
fi of c,
a, d, and f are stored row-wise in the MATLAB matrices c, a, d, and
f. The case of identity, diagonal, and symmetric matrices are handled
as special cases. For the tensor cijkl this
applies both to the indices i and j, and to the
indices k and l.
Partial Differential Equation Toolbox software does not check the ellipticity of the problem, and it is quite possible to define a system that is not elliptic in the mathematical sense. The preceding procedure that describes the scalar case is applied to each component of the system, yielding a symmetric positive definite system of equations whenever the differential system possesses these characteristics.
The boundary conditions now in general are mixed, i.e., for each point on the boundary a combination of Dirichlet and generalized Neumann conditions,
For 2-D systems, the notation represents an N-by-1 matrix with (i,1)-component
where the outward normal vector of the boundary is .
For 3-D systems, the notation represents an N-by-1 matrix with (i,1)-component
where the outward normal to the boundary is
There are M Dirichlet conditions and the h-matrix is M-by-N, M ≥ 0. The generalized Neumann condition contains a source , where the Lagrange multipliers μ are computed such that the Dirichlet conditions become satisfied. In a structural mechanics problem, this term is exactly the reaction force necessary to satisfy the kinematic constraints described by the Dirichlet conditions.
The rest of this section details the treatment of the Dirichlet conditions and may be skipped on a first reading.
Partial Differential Equation Toolbox software supports two implementations of Dirichlet conditions. The simplest is the “Stiff Spring” model, so named for its interpretation in solid mechanics. See Elliptic Equations for the scalar case, which is equivalent to a diagonal h-matrix. For the general case, Dirichlet conditions
hu = r
are approximated by adding a term
to the equations KU = F, where L is a large number such as 104 times a representative size of the elements of K.
When this number is increased, hu = r will be more accurately satisfied, but the potential ill-conditioning of the modified equations will become more serious.
The second method is also applicable to general mixed conditions with nondiagonal h, and is free of the ill-conditioning, but is more involved computationally. Assume that there are Np nodes in the mesh. Then the number of unknowns is NpN = Nu. When Dirichlet boundary conditions fix some of the unknowns, the linear system can be correspondingly reduced. This is easily done by removing rows and columns when u values are given, but here we must treat the case when some linear combinations of the components of u are given, hu = r. These are collected into HU = R where H is an M-by-Nu matrix and R is an M-vector.
With the reaction force term the system becomes
KU +H´ µ = F
HU = R.
The constraints can be solved for M of the U-variables, the remaining called V, an Nu – M vector. The null space of H is spanned by the columns of B, and U = BV + ud makes U satisfy the Dirichlet conditions. A permutation to block-diagonal form exploits the sparsity of H to speed up the following computation to find B in a numerically stable way. µ can be eliminated by pre-multiplying by B´ since, by the construction, HB = 0 or B´H´ = 0. The reduced system becomes
B´ KBV = B´ F – B´Kud
which is symmetric and positive definite if K is.
The finite element method for 3-D geometry is similar to the 2-D method described in Elliptic Equations. The main difference is that the elements in 3-D geometry are tetrahedra, which means that the basis functions are different from those in 2-D geometry.
It is convenient to map a tetrahedron to a canonical tetrahedron with a local coordinate system (r,s,t).

In local coordinates, the point p1 is at (0,0,0), p2 is at (1,0,0), p3 is at (0,1,0), and p4 is at (0,0,1).
For a linear tetrahedron, the basis functions are
For a quadratic tetrahedron, there are additional nodes at the edge midpoints.

The corresponding basis functions are
As in the 2-D case, a 3-D basis function ϕi takes the value 0 at all nodes j, except for node i, where it takes the value 1.
Version History
Introduced before R2006aassempde is not recommended. Use solvepde instead. There are no plans to remove
assempde.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)