assembleFEMatrices
Assemble finite element matrices
Syntax
Description
FEM = assembleFEMatrices(___,state)state structure array. The
function uses the time field of
the structure for time-dependent models and the
solution field u for nonlinear
models. You can use this argument with any of the
previous syntaxes.
Examples
Create a PDE model for the Poisson equation on an L-shaped membrane with zero Dirichlet boundary conditions.
model = createpde; geometryFromEdges(model,@lshapeg); specifyCoefficients(model,m=0,d=0,c=1,a=0,f=1); applyBoundaryCondition(model,"dirichlet", ... edge=1:model.Geometry.NumEdges, ... u=0);
Generate a mesh and obtain the default finite element matrices for the problem and mesh.
generateMesh(model,Hmax=0.2); FEM = assembleFEMatrices(model)
FEM = struct with fields:
K: [401×401 double]
A: [401×401 double]
F: [401×1 double]
Q: [401×401 double]
G: [401×1 double]
H: [80×401 double]
R: [80×1 double]
M: [401×401 double]
Make computations faster by specifying which finite element matrices to assemble.
Create an femodel object for steady-state thermal analysis and include the geometry of the built-in function squareg.
model = femodel(AnalysisType="thermalSteady", ... Geometry=@squareg);
Plot the geometry with the edge labels.
pdegplot(model,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])
Specify the thermal conductivity of the material and the internal heat source.
model.MaterialProperties = ...
materialProperties(ThermalConductivity=0.2);
model.FaceLoad = faceLoad(Heat=10);Set the boundary conditions.
model.EdgeBC([1,3]) = edgeBC(Temperature=100);
Generate a mesh.
model = generateMesh(model);
Assemble the stiffness and mass matrices.
FEM_KM = assembleFEMatrices(model,"KM")FEM_KM = struct with fields:
K: [1529×1529 double]
M: [1529×1529 double]
Now, assemble the finite element matrices M, K, A, and F.
FEM_MKAF = assembleFEMatrices(model,"MKAF")FEM_MKAF = struct with fields:
M: [1529×1529 double]
K: [1529×1529 double]
A: [1529×1529 double]
F: [1529×1 double]
The four matrices M, K, A, and F correspond to discretized versions of the PDE coefficients m, c, a, and f. These four matrices also represent the domain of the finite-element model of the PDE. Instead of specifying them explicitly, you can use the domain argument.
FEMd = assembleFEMatrices(model,"domain")FEMd = struct with fields:
M: [1529×1529 double]
K: [1529×1529 double]
A: [1529×1529 double]
F: [1529×1 double]
The four matrices Q, G, H, and R, correspond to discretized versions of q, g, h, and r in the Neumann and Dirichlet boundary condition specification. These four matrices also represent the boundary of the finite-element model of the PDE. Use the boundary argument to assemble only these matrices.
FEMb = assembleFEMatrices(model,"boundary")FEMb = struct with fields:
H: [74×1529 double]
R: [74×1 double]
G: [1529×1 double]
Q: [1529×1529 double]
Create a PDE model for the Poisson equation on an L-shaped membrane with zero Dirichlet boundary conditions.
model = createpde; geometryFromEdges(model,@lshapeg); specifyCoefficients(model,m=0,d=0,c=1,a=0,f=1); applyBoundaryCondition(model,"dirichlet", ... Edge=1:model.Geometry.NumEdges, ... u=0);
Generate a mesh.
generateMesh(model,Hmax=0.2);
Obtain the finite element matrices after imposing the boundary condition using the null-space approach. This approach eliminates the Dirichlet degrees of freedom and provides a reduced system of equations.
FEMn = assembleFEMatrices(model,"nullspace")FEMn = struct with fields:
Kc: [321×321 double]
Fc: [321×1 double]
B: [401×321 double]
ud: [401×1 double]
M: [321×321 double]
Obtain the solution to the PDE using the nullspace finite element matrices.
un = FEMn.B*(FEMn.Kc\FEMn.Fc) + FEMn.ud;
Compare this result to the solution given by solvepde. The two solutions are identical.
u1 = solvepde(model); norm(un - u1.NodalSolution)
ans = 0
Obtain the finite element matrices after imposing the boundary condition using the stiff-spring approach. This approach retains the Dirichlet degrees of freedom, but imposes a large penalty on them.
FEMs = assembleFEMatrices(model,"stiff-spring")FEMs = struct with fields:
Ks: [401×401 double]
Fs: [401×1 double]
M: [401×401 double]
Obtain the solution to the PDE using the stiff-spring finite element matrices. This technique gives a less accurate solution.
us = FEMs.Ks\FEMs.Fs; norm(us - u1.NodalSolution)
ans = 0.0098
Assemble finite element matrices for the first and last time steps of a transient structural problem.
Create the geometry and plot a cylinder geometry.
gm = multicylinder(0.01,0.05);
addVertex(gm,Coordinates=[0,0,0.05]);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5)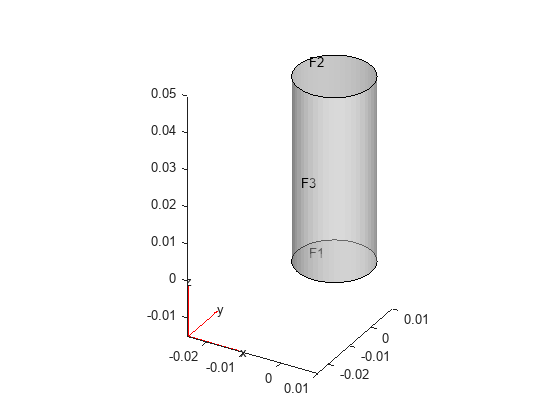
Create an femodel object for transient structural analysis and include the geometry in the model.
model = femodel(AnalysisType="structuralTransient", ... Geometry=gm);
Specify Young's modulus and Poisson's ratio.
model.MaterialProperties = ... materialProperties(YoungsModulus=201E9, ... PoissonsRatio=0.3, ... MassDensity=7800);
Specify that the bottom of the cylinder is a fixed boundary.
model.FaceBC(1) = faceBC(Constraint="fixed");Create a function specifying a harmonic pressure load.
function Tn = sinusoidalLoad(load,location,state,Frequency,Phase) if isnan(state.time) Tn = NaN*(location.nx); return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Transient model excited with harmonic load Tn = load.*sin(Frequency.*state.time + Phase); end
Apply the harmonic pressure on the top of the cylinder.
Pressure = 5e7;
Frequency = 50;
Phase = 0;
pressurePulse = @(location,state) ...
sinusoidalLoad(Pressure,location,state,Frequency,Phase);
model.FaceLoad(2) = faceLoad(Pressure=pressurePulse);Specify the zero initial displacement and velocity.
model.CellIC = cellIC(Displacement=[0;0;0], ...
Velocity=[0;0;0]);Generate a linear mesh.
model = generateMesh(model,GeometricOrder="linear");Assemble the finite element matrices for the initial time step.
tlist = linspace(0,1,300); state.time = tlist(1); FEM_domain = assembleFEMatrices(model,state)
FEM_domain = struct with fields:
K: [6645×6645 double]
A: [6645×6645 double]
F: [6645×1 double]
Q: [6645×6645 double]
G: [6645×1 double]
H: [252×6645 double]
R: [252×1 double]
M: [6645×6645 double]
Pressure applied at the top of the cylinder is the only time-dependent quantity in the model. To model the dynamics of the system, assemble the boundary-load finite element matrix G for the initial, intermediate, and final time steps.
state.time = tlist(1);
FEM_boundary_init = assembleFEMatrices(model,"G",state)FEM_boundary_init = struct with fields:
G: [6645×1 double]
state.time = tlist(floor(length(tlist)/2));
FEM_boundary_half = assembleFEMatrices(model,"G",state)FEM_boundary_half = struct with fields:
G: [6645×1 double]
state.time = tlist(end);
FEM_boundary_final = assembleFEMatrices(model,"G",state)FEM_boundary_final = struct with fields:
G: [6645×1 double]
Assemble finite element matrices for a heat transfer problem with temperature-dependent thermal conductivity.
Create a 2-D geometry by drawing one rectangle the size of the block and a second rectangle the size of the slot.
r1 = [3 4 -.5 .5 .5 -.5 -.8 -.8 .8 .8]; r2 = [3 4 -.05 .05 .05 -.05 -.4 -.4 .4 .4]; gdm = [r1; r2]';
Subtract the second rectangle from the first to create the block with a slot.
g = decsg(gdm,'R1-R2',['R1'; 'R2']');
Create an femodel object for steady-state thermal analysis and include the geometry in the model.
model = femodel(AnalysisType="thermalSteady", ... Geometry=g);
Plot the geometry.
pdegplot(model,EdgeLabels="on");
axis([-.9 .9 -.9 .9]);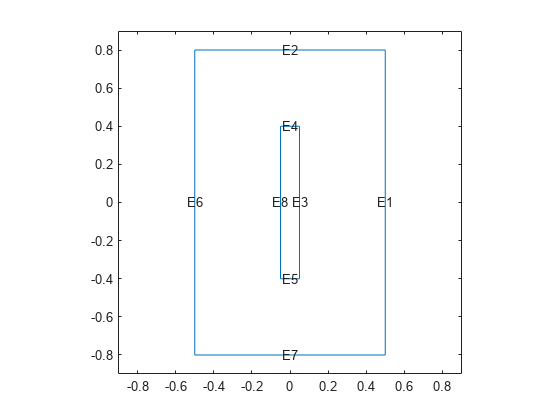
Set the temperature on the left edge to 100 degrees. Set the heat flux out of the block on the right edge to -10. The top and bottom edges and the edges inside the cavity are all insulated: there is no heat transfer across these edges.
model.EdgeBC(6) = edgeBC(Temperature=100); model.EdgeLoad(1) = edgeLoad(Heat=-10);
Specify the thermal conductivity of the material as a simple linear function of temperature u.
k = @(~,state) 0.7+0.003*state.u;
model.MaterialProperties = ...
materialProperties(ThermalConductivity=k);Specify the initial temperature.
model.FaceIC = faceIC(Temperature=0);
Generate a mesh.
model = generateMesh(model);
Calculate the steady-state solution.
Rnonlin = solve(model);
Because the thermal conductivity is nonlinear (depends on the temperature), compute the system matrices corresponding to the converged temperature. Assign the temperature distribution to the u field of the state structure array. Because the u field must contain a row vector, transpose the temperature distribution.
state.u = Rnonlin.Temperature.';
Assemble finite element matrices using the temperature distribution at the nodal points.
FEM = assembleFEMatrices(model,"nullspace",state)FEM = struct with fields:
Kc: [1285×1285 double]
Fc: [1285×1 double]
B: [1308×1285 double]
ud: [1308×1 double]
M: [1285×1285 double]
Compute the solution using the system matrices to verify that they yield the same temperature as Rnonlin.
u = FEM.B*(FEM.Kc\FEM.Fc) + FEM.ud;
Compare this result to the solution given by solve.
norm(u - Rnonlin.Temperature)
ans = 5.7842e-06
Input Arguments
Model object, specified as an
femodel or
PDEModel object.
assembleFEMatrices does
not support assembling FE matrices for 3-D
magnetostatic analysis.
Example: model =
femodel
Example: model =
createpde
Method for including boundary conditions, specified as "none",
"nullspace", or
"stiff-spring". For more
information, see Algorithms.
Example: FEM = assembleFEMatrices(model,"nullspace")
Data Types: char | string
Matrices to assemble, specified as:
Matrix identifiers, such as
"F","MKF","K", and so on — Assemble the corresponding matrices. Each uppercase letter represents one matrix:K,A,F,Q,G,H,R,M, andT. You can combine several letters into one character vector or string, such as"MKF"."boundary"— Assemble all matrices related to geometry boundaries."domain"— Assemble all domain-related matrices.
Example: FEM =
assembleFEMatrices(model,"KAF")
Data Types: char | string
Time for time-dependent models and solution for nonlinear models, specified in a structure array. The array fields represent the following values:
state.timecontains a nonnegative number specifying the time value for time-dependent models.state.ucontains a solution matrix of size N-by-Np that can be used to assemble matrices in a nonlinear problem setup, where coefficients are functions ofstate.u. Here, N is the number of equations in the system, and Np is the number of nodes in the mesh.
Example: state.time = tlist(end);
FEM =
assembleFEMatrices(model,"boundary",state)
Output Arguments
Finite element matrices, returned as a structural array. Use the bcmethod
and matrices arguments to
specify which finite element matrices you want to
assemble.
The fields in the structural array depend
on bcmethod:
If the value is
"none", then the fields areK,A,F,Q,G,H,R, andM.If the value is
"nullspace", then the fields areKc,Fc,B,ud, andM.If the value is
"stiff-spring", then the fields areKs,Fs, andM.
The fields in the structural array also
depend on matrices:
If the value is
boundary, then the fields are all matrices related to geometry boundaries.If the value is
domain, then the fields are all domain-related matrices.If the value is a matrix identifier or identifiers, such as
"F","MKF","K", and so on, then the fields are the corresponding matrices.
For more information, see Algorithms.
Algorithms
Partial Differential Equation Toolbox™ solves equations of the form
and eigenvalue equations of the form
with the Dirichlet boundary conditions, hu = r, and Neumann boundary conditions, .
assembleFEMatrices returns the following full finite element matrices and
vectors that represent the corresponding PDE problem:
Kis the stiffness matrix, the integral of the discretized version of theccoefficient.Mis the mass matrix, the integral of the discretized version of themordcoefficients.Mis nonzero for time-dependent and eigenvalue problems.Ais the integral of the discretized version of theacoefficient.Fis the integral of the discretized version of thefcoefficient. For thermal, electromagnetic, and structural problems,Fis a source or body load vector.Qis the integral of the discretized version of theqterm in a Neumann boundary condition.Gis the integral of the discretized version of thegterm in a Neumann boundary condition. For structural problems,Gis a boundary load vector.The
HandRmatrices come directly from the Dirichlet conditions and the mesh.
The "nullspace" technique eliminates
Dirichlet conditions from the problem using a linear algebra
approach. It generates the combined finite-element matrices
Kc, Fc, B, and vector ud corresponding to the reduced system
Kc*u = Fc, where Kc =
B'*(K + A + Q)*B, and Fc =
B'*((F + G)-(K + A + Q)*ud). The
B matrix spans the null space
of the columns of H (the Dirichlet
condition matrix representing h*ud = r).
The R vector represents the Dirichlet
conditions in H*ud = R. The
ud vector has the size of the
solution vector. Its elements are zeros everywhere except at
Dirichlet degrees-of-freedom (DoFs) locations where they
contain the prescribed values.
From the "nullspace" matrices, you can
compute the solution u as
u = B*(Kc\Fc) +
ud.
If you assembled a particular set of matrices, for example
G and M, you
can impose the boundary conditions on G
and M as follows. First, compute the
nullspace of columns of H.
[B,Or] = pdenullorth(H);
ud = Or*((H*Or\R)); % Vector with known value of the constraint DoF.Then use the B matrix as follows. To
eliminate Dirichlet degrees of freedom from the load vector
G, use:
GwithBC = B'*G
To eliminate Dirichlet degrees of freedom from mass matrix, use:
M = B'*M*B
You can eliminate Dirichlet degrees of freedom from other vectors and matrices using the same technique.
The "stiff-spring" technique converts
Dirichlet boundary conditions to Neumann boundary conditions
using a stiff-spring approximation. It returns a matrix
Ks and a vector
Fs that together represent a
different type of combined finite element matrices. The
approximate solution is u = Ks\Fs.
Compared to the "nullspace" technique,
the "stiff-spring" technique generates
matrices more quickly, but generally gives less accurate
solutions.
If the number of nodes in a model is
NumNodes, and the number of equations is
N, then the length of column
vectors u and ud is
N*NumNodes. The toolbox assigns
the IDs to the degrees of freedom in u
and ud:
Entries from 1 to
NumNodescorrespond to the first equation.Entries from
NumNodes+1to2*NumNodescorrespond to the second equation.Entries from
2*NumNodes+1to3*NumNodescorrespond to the third equation.
The same approach applies to all other entries, up to
N*NumNodes.
For example, in a 3-D structural model, the length of a solution
vector u is
3*NumNodes. The first
NumNodes entries correspond to
the x-displacement at each node, the next
NumNodes entries correspond to
the y-displacement, and the next
NumNodes entries correspond to
the z-displacement.
In thermal analysis, the m and
a coefficients are zeros. The
thermal conductivity maps to the c
coefficient. The product of the mass density and the
specific heat maps to the d coefficient.
The internal heat source maps to the f
coefficient. The temperature on a boundary corresponds to
the Dirichlet boundary condition term r
with h = 1. Various forms of boundary
heat flux, such as the heat flux itself, emissivity, and
convection coefficient, map to the Neumann boundary
condition terms q and
g.
In structural analysis, the a coefficient is
zero. Young's modulus and Poisson's ratio map to the
c coefficient. The mass density
maps to the m coefficient. The body loads
map to the f coefficient. Displacements,
constraints, and components of displacement along the axes
map to the Dirichlet boundary condition terms
h and r.
Boundary loads, such as pressure, surface tractions, and
translational stiffnesses, correspond to the Neumann
boundary condition terms q and
g. When you specify the damping
model by using the Rayleigh damping parameters
Alpha and
Beta, the discretized damping
matrix C is computed by using the mass
matrix M and the stiffness matrix
K as C = Alpha*M +
Beta*K. Hysteretic (structural) damping
contributes to the stiffness matrix K,
which becomes complex.
In electrostatic and magnetostatic analyses, the
m, a, and
d coefficients are zeros. The
relative permittivity and relative permeability map to the
c coefficient. The charge
density and current density map to the f
coefficient. The voltage and magnetic potential on a
boundary correspond to the Dirichlet boundary condition term
r with h =
1.
Note
Assembling FE matrices does not work for harmonic analysis and 3-D magnetostatic analysis.
Version History
Introduced in R2016aassembleFEMatrices will no longer accept
StructuralModel,
ThermalModel, and
ElectromagneticModel. These
objects will be removed. Use an femodel object instead.
The unified finite element model workflow defines the type of a
problem and all of its parameters as the properties of an
femodel object. This object
enables you to specify physical parameters for structural,
thermal, and electromagnetic types of analyses. The solver
in the unified workflow uses only the parameters
(properties) appropriate for the current analysis type while
ignoring all other properties. If you switch the analysis
type by setting the AnalysisType property
of the model, the solver uses the appropriate set of
properties corresponding to the new analysis type.
For more help migrating your existing code that uses
StructuralModel,
ThermalModel, or
ElectromagneticModel to the
unified finite element workflow, see Migration from Domain-Specific to Unified Workflow.
The function accepts femodel objects used in Unified Modeling.
The function now can assemble matrices using input time or solution for a time-dependent or nonlinear model, respectively. It also can assemble a subset of matrices, such as updated load only or stiffness only, to save computation time.
The function accepts thermal and structural models with time- and solution-independent coefficients.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)