Mesh Data as [p,e,t] Triples

Partial Differential Equation Toolbox™ uses meshes with triangular elements for 2-D geometries and meshes with tetrahedral elements for 3-D geometries. Earlier versions of Partial Differential Equation Toolbox use meshes in the form of a [p,e,t] triple. The matrices p, e, and t represent the points (nodes), elements, and triangles or tetrahedra of a mesh, respectively. Later versions of the toolbox support the [p,e,t] meshes for compatibility reasons.

Note

New features might not be compatible with the legacy workflow. For description of the mesh data in the recommended workflow, see Mesh Data.

The mesh data for a 2-D mesh has these components:

• p (points, the mesh nodes) is a 2-by-Np matrix of nodes, where Np is the number of nodes in the mesh. Each column p(:,k) consists of the x-coordinate of point k in p(1,k) and the y-coordinate of point k in p(2,k).

• e (edges) is a 7-by-Ne matrix of edges, where Ne is the number of edges in the mesh. The mesh edges in e and the edges of the geometry have a one-to-one correspondence. The e matrix represents the discrete edges of the geometry in the same manner as the t matrix represents the discrete faces. Each column in the e matrix represents one edge.

  • e(1,k) is the index of the first point in mesh edge k.

  • e(2,k) is the index of the second point in mesh edge k.

  • e(3,k) is the parameter value at the first point of edge k. The parameter value is related to the arc length along the geometric edge.

  • e(4,k) is the parameter value at the second point of edge k.

  • e(5,k) is the ID of the geometric edge containing the mesh edge. You can see edge IDs by using the command pdegplot(geom,'EdgeLabels','on').

  • e(6,k) is the subdomain number on the left side of the edge. The direction along the edge is given by increasing parameter values. The subdomain 0 is the exterior of the geometry.

  • e(7,k) is the subdomain number on the right side of the edge.

• t (triangles) is a 4-by-Nt matrix of triangles or a 7-by-Nt matrix of triangles, depending on whether you call generateMesh with the GeometricOrder name-value pair set to 'quadratic' or 'linear', respectively. initmesh creates only 'linear' elements, which have size 4-by-Nt. Nt is the number of triangles in the mesh. Each column of t contains the indices of the points in p that form the triangle. The exception is the last entry in the column, which is the subdomain number. Triangle points are ordered as shown.

• 

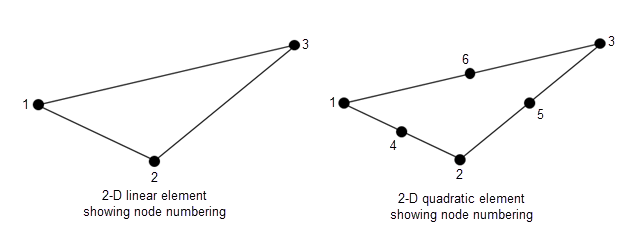
The mesh data for a 3-D mesh has these components:

• p (points, the mesh nodes) is a 3-by-Np matrix of nodes, where Np is the number of nodes in the mesh. Each column p(:,k) consists of the x-coordinate of point k in p(1,k), the y-coordinate of point k in p(2,k), and the z-coordinate of point k in p(3,k).

• e is an object that associates the mesh faces with the geometry boundaries. Partial Differential Equation Toolbox functions use this association when converting the boundary conditions, which you set on geometry boundaries, to the mesh boundary faces.

• t (tetrahedra) is either an 11-by-Nt matrix of tetrahedra or a 5-by-Nt matrix of tetrahedra, depending on whether you call generateMesh with the GeometricOrder name-value pair set to 'quadratic' or 'linear', respectively. Nt is the number of tetrahedra in the mesh. Each column of t contains the indices of the points in p that form the tetrahedron. The exception is the last element in the column, which is the subdomain number. Tetrahedron points are ordered as shown.

You can create a [p,e,t] mesh by using one of these approaches:

• Use the initmesh function to create a 2-D [p,e,t] mesh.

• Use the generateMesh function to create a 2-D or 3-D mesh as a FEMesh object. Then use the meshToPet function to convert the mesh to a [p,e,t] mesh.