Estimate Initial Conditions for Simulating Identified Models
When you simulate a dynamic system that does not start from rest, you must initialize that simulation to match the starting conditions. For example, you may be comparing your simulated response to measured data, or to a previous simulation or computation. You might want to start your simulation at a steady-state condition, or continue a simulation from a previous simulation.
Summary of Initial-Condition Estimation Approaches
System Identification Toolbox™ provides multiple techniques for determining initial conditions (ICs) to use. These techniques include using:
Model identification results
Current or past input/output data measurements
State information from previous simulations
The following table summarizes what approaches are available and when to use them. For conciseness, this table uses the term "simulating" broadly to mean "simulating or predicting." For more information, see Simulate and Predict Identified Model Output.
Approaches for Estimating Initial Conditions
| When to Use | Approach | Method Summary |
|---|---|---|
You are simulating an idss,idtf, idproc,
idpoly, or
idgrey model
response using the same input data with which you identified
your model. | Extract ICs from model identification results (returned values or estimation report). Estimation returns IC information in one of the following forms.
|
Examples: Resolve Fit Value Differences Between Model Identification and compare Command Apply Initial Conditions When Simulating Identified Linear Models |
You want to reproduce the results generated by compare (or
generated by the Model Output plot in the
app). | Use returned ICs from
|
Examples: Match Output of compare Command and Nonlinear ARX Model Block Apply Initial Conditions When Simulating Identified Linear Models |
| You are simulating model response to a given input signal, and want to start the simulation at a point that leads to the closest match to a given output signal. | Use Use
If the original model is
|
Examples: Apply Initial Conditions When Simulating Identified Linear Models Estimate Initial Conditions for Linear Model Using Measured Data |
| You are continuing a simulation, such as for online
processing. You are using a split data set, such as for nlarx model
when findstates is too computationally
expensive. | data2state
If original model is idtf, idproc, or
idpoly, convert to state-space form
first using idss.
You can also use data2state implicitly by specifying
your past data as a proxy for initial conditions when using
sim or predict with any
dynamic model.For more information, see Estimate Initial Conditions from Measured Data. | sys_ss =
idss(sys)x0 =
data2state(sys,z_p)or IO
=
struct or
opt = predictOptions
('InitialCondition',IO).
examples: Estimate Initial Conditions for a Nonlinear ARX Model, Understand Use of Historical Data for Model Simulation |
| You are working with a continuing simulation, and want to
base initial conditions for the current simulation segment on
the previous segment. You intend to start your main simulation in steady state, and you want to have a prequel which simulates the run-up to steady state from rest. | Use state information from previous simulation or
presimulation. If original model is idtf, idproc,
or idpoly, convert to state-space form
first using idss.
For more information, see Use Initial Conditions from Past State Information. | sys_ss =
idss(sys)x0 =
x(end) from [y,y_sd,x] =
sim(sys_ss,z_p)example: Continue Simulation of an Identified Model Using Past States |
Initial-Condition Estimation Techniques
The preceding table calls out various techniques for initial-condition estimation. The following sections summarize these techniques by the estimation data source.
Estimate Initial Conditions from Measured Data
Estimate the initial conditions from the measurement data from which you are getting your simulation inputs. Techniques include the following.
Extract initial conditions from model-identification results, such as from the identification report for your model or as returned values from
compare. X0 represents an initial state vector and IC represents aninitialConditionobject. For examples, see Resolve Fit Value Differences Between Model Identification and compare Command, Match Output of compare Command and Nonlinear ARX Model Block, and Apply Initial Conditions When Simulating Identified Linear Models.Estimate initial conditions using measured input/output data, using the function
findstatesto estimate the initial states consistent with the data set. For an example, see Estimate Initial Conditions for Linear Model Using Measured Data.
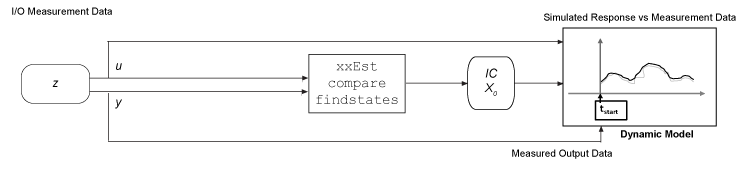
Estimate Initial Conditions from Past Measurement Data
Estimate the initial conditions from the measurement data immediately preceding your simulation start. Techniques include the following.
Using the function
data2stateto estimate that data set end state. The past end state then becomes the initial state for follow-on simulation. For an example, see Estimate Initial Conditions for a Nonlinear ARX Model.Using your past data as a proxy for initial conditions when using
simorpredict. When you run your simulation, the model internally callsdata2statefor you. For an example, see Understand Use of Historical Data for Model Simulation.Splitting the data set you are using into two parts. Make the first part just large enough to allow
data2stateto calculate an accurate end state. This split-data approach can be much less computationally intensive than usingfindstateson the full data set, especially for nonlinear ARX models. For an example, see Estimate Initial Conditions for a Nonlinear ARX Model.
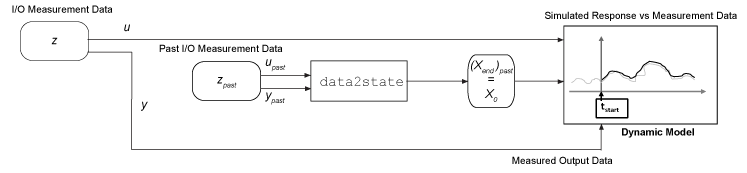
Use Initial Conditions from Past State Information
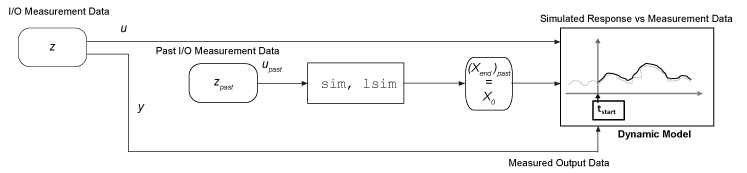
Use state information from previous simulations or presimulations. If no previous simulation is available, you can presimulate from rest or a known initial condition up to the point of your simulation start. The end states of the past or presimulation are the starting states for the simulation you want to perform. For an example, see Continue Simulation of an Identified Model Using Past States.
Estimate Initial Conditions for Simulating Linear Models
The findstates and data2state functions
are the most general tools for determining initial or end states from any
measurements of input/output data. However, to use these functions, you must have a
model structure that includes explicit state representation. Linear models other
than idss and idgrey do not use explicit
states. To find the equivalent initial states, you can convert these models to
idss models and find the initial states from the
idss versions. As an alternative to
findstates, you can also use compare
to obtain initial conditions without converting your models into state-space form.
For these models, compare returns an initialCondition object that contains information on the model free
response, in state-space form, and the corresponding initial states.
After you estimate the initial conditions, you can incorporate them into your command-line simulation syntax, your Simulink® model, or the System Identification app.
The following examples illustrate initial-condition estimation for linear models.
The first example uses findstates and
compare. The second and third examples use historical data.
That is, the examples determine initial conditions from the data immediately
preceding the simulation start time.
Estimate Initial Conditions for Linear Model Using Measured Data
Use different methods to obtain initial conditions for a linear model and compare the results.
Estimate a transfer function for measured data. Return the initial conditions in ic.
load iddata1 z1; [sys,ic] = tfest(z1,3); ic
ic =
initialCondition with properties:
A: [3×3 double]
X0: [3×1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic.X0
ans = 3×1
-1.7569
2.6195
-6.5177
sys is a continuous-time identified transfer function (idtf) model. ic is an initialCondition object. An initialCondition object represents the free response of the system in state-space form. The object includes the converted A and C state-space matrices that correspond to sys and the estimated initial state vector X0.
You can also use findstates to find initial conditions for linear models, but only if they are in idss or idgrey form.
Convert sys to state-space form.
sys_ss = idss(sys);
Use findstates to estimate the initial states.
X0 = findstates(sys_ss,z1)
X0 = 3×1
-1.7569
2.6195
-6.5177
Now use compare to estimate the initial states, using the original transfer function model.
[y_tf,fit,ic2] = compare(z1,sys); ic2
ic2 =
initialCondition with properties:
A: [3×3 double]
X0: [3×1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic2.X0
ans = 3×1
-1.7569
2.6195
-6.5177
The initial state vectors are identical in all three cases.
Understand Use of Historical Data for Model Simulation
Use historical input-output data as a proxy for initial conditions when simulating your model. You first simulate using the sim command and specify the historical data using the simOptions option set. You then reproduce the simulated output by manually mapping the historical data to initial states.
Load a two-input, one-output data set.
load iddata7 z7
Identify a fifth-order state-space model using the data.
sys = n4sid(z7,5);
Split the data set into two parts.
zA = z7(1:15); zB = z7(16:end);
Simulate the model using the input signal in zB.
uSim = zB;
Simulation requires initial conditions. The signal values in zA are the historical data, that is, they are the input and output values for the time immediately preceding data in zB. Use zA as a proxy for the required initial conditions.
IO = struct('Input',zA.InputData,'Output',zA.OutputData); opt = simOptions('InitialCondition',IO);
Simulate the model.
ysim = sim(sys,uSim,opt);
Now reproduce the output by manually mapping the historical data to initial states of sys. To do so, use the data2state command.
xf = data2state(sys,zA);
xf contains the state values of sys at the time instant immediately after the most recent data sample in zA.
Simulate the system using xf as the initial states.
opt2 = simOptions('InitialCondition',xf);
ysim2 = sim(sys,uSim,opt2);Plot the output of the sim command ysim and the manually computed results ysim2.
plot(ysim,'b',ysim2,'--r')

ysim2 is the same as ysim.
Continue Simulation of an Identified Model Using Past States
Estimate the initial conditions for a simulation segment of an identified model by using the end states of the previous simulation segment.
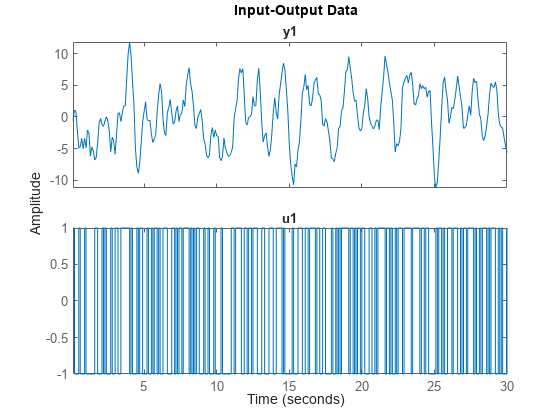
Load data z1, which is an iddata object containing input and output data. Estimate a fifth-order linear model from the data.
load iddata1 z1 plot(z1)
sys = n4sid(z1,5);
Divide the data into two segments. One segment z1past represents data for a past simulation, and starts at rest. The second segment z1next represents data for a follow-on simulation.
z1past = z1(1:150); z1next = z1(150:300);
Simulate the response to the input data in z1next without specifying initial conditions.
ynext_no_ic = sim(z1next,sys);
plot(ynext_no_ic,z1next)
legend
title('Simulation Continuation Without Setting ICs')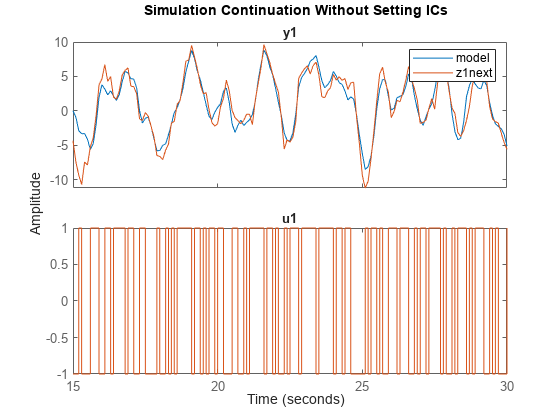
Now determine the end states, x0, for the response to z1past input.
[ypast,y_sd,xpast] = sim(z1past,sys); x0 = xpast(end,:)';
Use the end states to specify the initial states for the follow-on response to z1next.
opt = simOptions('InitialCondition',x0); ynext_ic = sim(z1next,sys,opt); figure plot(ynext_ic,z1next) legend title('Simulation Continuation with Sychronized ICs')

Estimate Initial Conditions for Simulating Hammerstein-Wiener and Nonlinear Grey-Box Models
When you are simulating a Hammerstein-Wiener or a nonlinear grey-box model and
want to use initial conditions consistent with a measurement data set
z, use findstates.
Simulate Hammerstein-Wiener Model in Simulink
Compare the simulated output of a Hammerstein-Wiener Model block to the measured output of a system. You improve the agreement between the measured and simulated responses by estimating initial state values.
Load the sample data.
load twotankdata
Create an iddata object from the sample data.
z1 = iddata(y,u,0.2,'Name','Two tank system');
Estimate a Hammerstein-Wiener model using the data.
mw1 = nlhw(z1,[1 5 3],idPiecewiseLinear,idPiecewiseLinear);
You can now simulate the output of the estimated model in Simulink using the input data in z1. To do so, open a preconfigured Simulink model.
model = 'ex_idnlhw_block';
open_system(model);

The model uses the Iddata Source, Hammerstein-Wiener Model, and Scope blocks. The following block parameters have been preconfigured to specify the estimation data, estimated model, and initial conditions:
Block parameters of Iddata Source block:
IDDATA Object -
z1Start time -
–1
Block parameters of Hammerstein-Wiener Model block:
Model -
mw1Initial conditions -
Zero(default)
Run the simulation.
View the difference between measured output and model output by using the Scope block.
simOut = sim(model);
open_system([model '/Scope'])

To improve the agreement between the measured and simulated responses, estimate an initial state vector for the model from the estimation data z1, using findstates. Specify the maximum number of iterations for estimation as 100. Specify the prediction horizon as Inf, so that the algorithm computes the initial states that minimize the simulation error.
opt = findstatesOptions; opt.SearchOptions.MaxIterations = 100; x0 = findstates(mw1,z1,Inf,opt);
Set the Initial conditions block parameter value of the Hammerstein-Wiener Model block to State Values. The default initial states are x0.
set_param([model '/Hammerstein-Wiener Model'],'IC','State values');
Run the simulation again, and view the difference between measured output and model output in the Scope block. The difference between the measured and simulated responses is now reduced.
simOut = sim(model);

Estimate Initial Conditions for Simulating Nonlinear ARX Models
When you are simulating a nonlinear ARX model and want to use initial conditions
consistent with a measurement data set z, you have a choice for
which approach to take.
You can use
findstates. For nonlinear ARX models however, this approach has the cost of being computationally expensive if the data set is large.X0 = findstates(m,z,Inf);
You can break the data set into two portions. Use the first
nxsamples of the input/output data as past data, wherenxis the largest regressor delay in the model. Then usedata2stateto compute the end state of the "past data." You are then able to simulate the model for the remainingnx+1:endinput data with whatever simulation approach you choose. Bothcompareand the System Identification app use this approach automatically for nonlinear ARX models.nx = max(getDelayInfo(m)); % Find the largest regressor delay past_data = z1(1:nx); X0 = data2state(mw1,z1(1:nx));The following example illustrates the use of split-data technique for a nonlinear ARX model.
Estimate Initial Conditions for a Nonlinear ARX Model
Use two different techniques to estimate the initial conditions for a nonlinear ARX model. Simulate each alongside the measurement data, and compare with a simulation that initializes at rest.
Load the input/output data z and plot it. Use the first 1000 points of z to estimate a nonlinear ARX model.
load twotankdata z = iddata(y,u,0.2); z1 = z(1:1000); plot(z1) title('Estimation data')

mdlnlarx = nlarx(z1,[5 1 3],idWaveletNetwork);
Extract the first 250 points of z1 (50 seconds) as z1sim for comparison simulations. Simulate mdlarx without setting initial conditions, and plot the response alongside the measured output in z1sim.
z1sim = z1(1:250); data_no_ic = sim(mdlnlarx,z1sim); plot(data_no_ic,z1sim) title('Nonlinear ARX Model with No Initial Condition Setting') grid on legend('location','se')
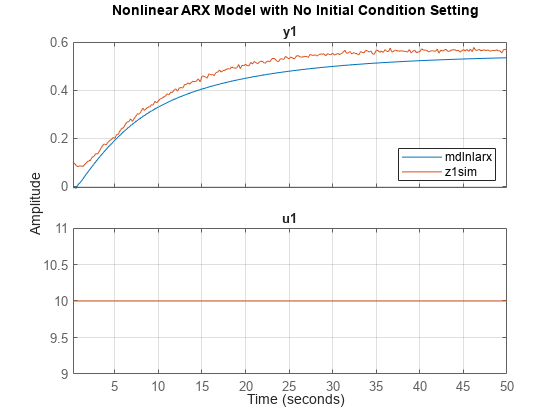
Use findstates to estimate the initial conditions. In order to minimize the simulation error, specify Inf for the prediction horizon. Then set the sim option for InitialCondition to the findstates results. Plot the response alongside the measured output.
x0fs = findstates(mdlnlarx,z1sim,Inf); opt = simOptions('InitialCondition',x0fs); data_fs = sim(mdlnlarx,z1sim,opt); figure plot(data_fs,z1sim) title('Nonlinear ARX Model with IC Estimation Using findstates') grid on legend('location','se')
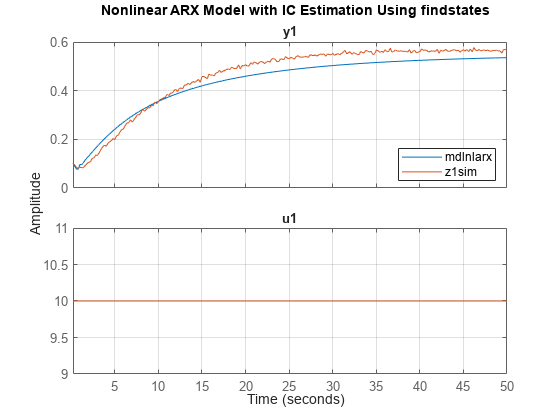
The response and the measured output now start at roughly the same point.
Now use the data2states method to estimate the initial conditions. First, break the data set into two portions. Use the first nx samples of z1sim as "past data", where nx is the largest regressor delay in the model.
nx = max(getDelayInfo(mdlnlarx))
nx = 5
z1past = z1sim(1:nx); z1sim2 = z1sim(nx+1:end);
Use data2state to compute the end state of the "past data." Simulate the response using input starting at z1sim(nx+1). Plot the response alongside the full z1sim measurement data so that you can compare with the findstates plot.
x0d2s = data2state(mdlnlarx,z1past); opt = simOptions('InitialCondition',x0d2s); data_d2s = sim(mdlnlarx,z1sim2,opt); figure plot(data_d2s,z1sim) title('Nonlinear ARX Model with IC Estimation Using data2state') grid on legend('location','se')
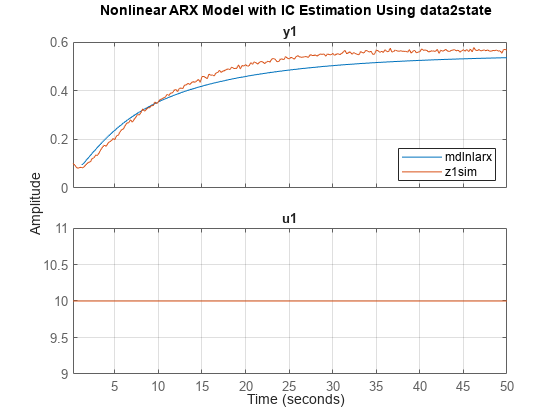
If you executed each section separately, you may find that the data2states method completed more quickly than the findstates method.
Now compare the responses for all three initial-condition cases.
plot(data_fs,data_d2s,data_no_ic) title('Nonlinear ARX model Responses for Three IC Approaches Compared') legend('location','se')
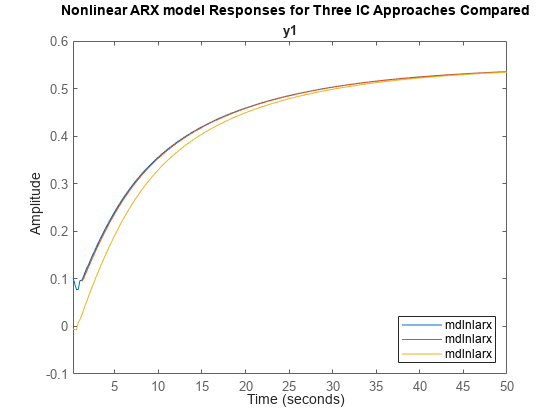
The responses for cases using findstates and data2state are virtually the same. The response for the case where the initial conditions were not set converges eventually, but not until after 30 seconds.
See Also
compare | compareOptions | sim | simOptions | predict | predictOptions | findstates | data2state