fixed.interpn
Interpolation for 1-D, 2-D, 3-D, and N-D gridded data in
ndgrid format
Since R2024a
Syntax
Description
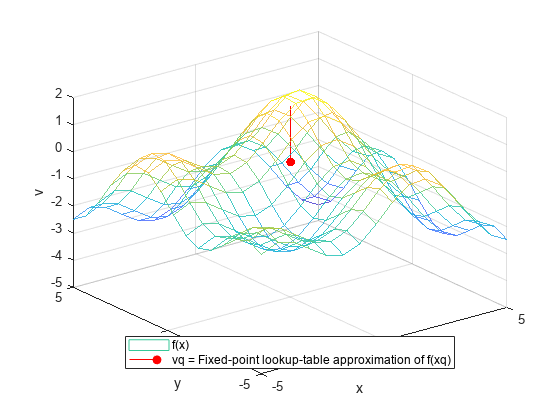
Vq = fixed.interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn)X1,X2,...,Xn contain the coordinates of the
sample points. V contains the corresponding function values at each
sample point. Xq1,Xq2,...,Xqn contain the coordinates of the query
points.
Vq = fixed.interpn(V,Xq1,Xq2,...,Xqn)V.
Use this syntax when you want to conserve memory and are not concerned about the absolute
distances between points.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2024a
See Also
fixed.interp1 | fixed.interp2 | fixed.interp3 | ndgrid | interpn