Cubic Spline Interpolation
Cubic Spline Interpolant of Smooth Data
Suppose you want to interpolate some smooth data, e.g., to
rng(6), x = (4*pi)*[0 1 rand(1,15)]; y = sin(x);
You can use the cubic spline interpolant obtained by
cs = csapi(x,y);
and plot the spline, along with the data, with the following code:
fnplt(cs);
hold on
plot(x,y,'o')
legend('cubic spline','data')
hold off
This produces a figure like the following.
Cubic Spline Interpolant of Smooth Data
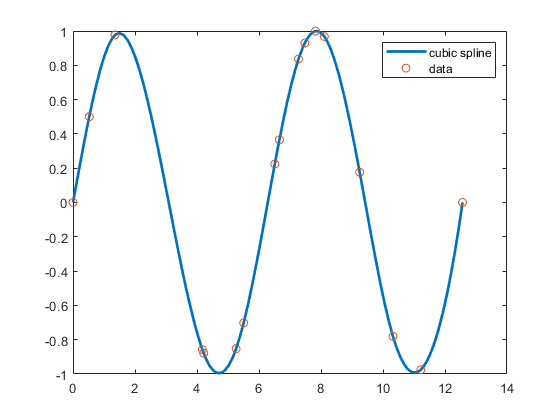
This is, more precisely, the cubic spline interpolant with the
not-a-knot end conditions, meaning that it is the unique piecewise
cubic polynomial with two continuous derivatives with breaks at all interior data
sites except for the leftmost and the rightmost one. It is the same
interpolant as produced by the MATLAB® spline command, spline(x,y).
Periodic Data
The sine function is 2π-periodic. To check how well your interpolant does on that score, compute, e.g., the difference in the value of its first derivative at the two endpoints,
diff(fnval(fnder(cs),[0 4*pi])) ans = -.0100
which is not so good. If you prefer to get an interpolant whose first and second
derivatives at the two endpoints, 0 and 4*pi, match, use
instead the command csape which permits specification of many different kinds
of end conditions, including periodic end conditions. So, use instead
pcs = csape(x,y,'periodic');
for which you get
diff(fnval(fnder(pcs),[0 4*pi]))
Output is ans = 0 as the difference of end slopes. Even the difference
in end second derivatives is small:
diff(fnval(fnder(pcs,2),[0 4*pi]))
Output is ans = -4.6074e-015.
Other End Conditions
Other end conditions can be handled as well. For example,
cs = csape(x,[3,y,-4],[1 2]);
provides the cubic spline interpolant with breaks at the ![]() and with its slope at the leftmost data site equal to 3, and its second
derivative at the rightmost data site equal to -4.
and with its slope at the leftmost data site equal to 3, and its second
derivative at the rightmost data site equal to -4.
General Spline Interpolation
If you want to interpolate at sites other than the breaks and/or
by splines other than cubic splines with simple knots, then you use the spapi command.
In its simplest form, you would say sp = spapi(k,x,y);
in which the first argument, k, specifies the order of
the interpolating spline; this is the number of coefficients in each
polynomial piece, i.e., 1 more than the nominal degree of its polynomial
pieces. For example, the next figure shows a linear, a quadratic,
and a quartic spline interpolant to your data, as obtained by the
statements
sp2 = spapi(2,x,y); fnplt(sp2,2), hold on
sp3 = spapi(3,x,y); fnplt(sp3,2,'k--'),
sp5 = spapi(5,x,y); fnplt(sp5,2,'r-.'), plot(x,y,'o')
legend('linear','quadratic','quartic','data'), hold off
Spline Interpolants of Various Orders of Smooth Data
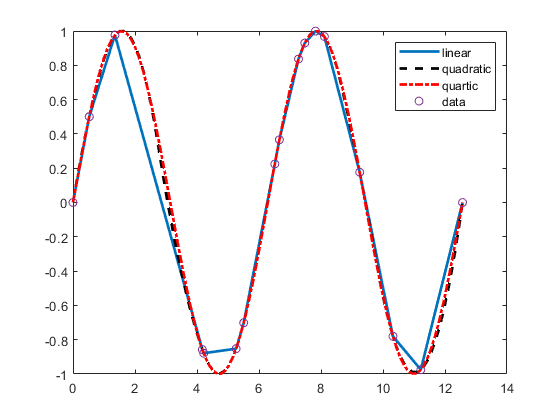
Even the cubic spline interpolant obtained from spapi is different from the one provided
by csapi and spline. To emphasize their difference,
compute and plot their second derivatives, as follows:
fnplt(fnder(spapi(4,x,y),2)), hold on,
fnplt(fnder(csapi(x,y),2),2,'k--'),plot(x,zeros(size(x)),'o')
legend('from spapi','from csapi','data sites'), hold off
This gives the following graph:
Second Derivative of Two Cubic Spline Interpolants of the Same Smooth Data
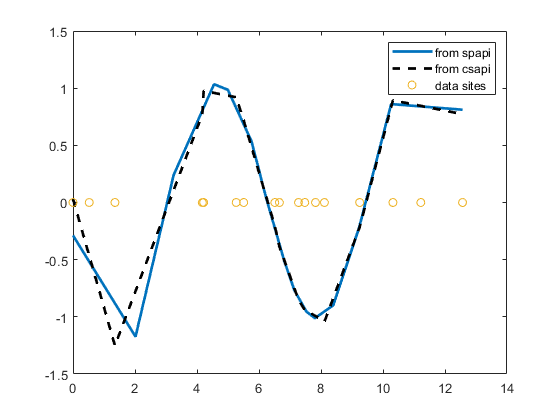
Since the second derivative of a cubic spline is a broken line,
with vertices at the breaks of the spline, you can see clearly that csapi places
breaks at the data sites, while spapi does not.
Knot Choices
It is, in fact, possible to specify explicitly just where the
spline interpolant should have its breaks, using the command sp
= spapi(knots,x,y); in which the sequence knots supplies,
in a certain way, the breaks to be used. For example, recalling that
you had chosen y to be sin(x),
the command
ch = spapi(augknt(x,4,2),[x x],[y cos(x)]);
provides a cubic Hermite interpolant to the sine function, namely
the piecewise cubic function, with breaks at all the x(i)'s,
that matches the sine function in value and slope
at all the x(i)'s. This makes the interpolant continuous
with continuous first derivative but, in general, it has jumps across
the breaks in its second derivative. Just how does this command know
which part of the data value array [y cos(x)] supplies
the values and which the slopes? Notice that the data site array here
is given as [x x], i.e., each data site appears
twice. Also notice that y(i) is associated with
the first occurrence of x(i), and cos(x(i)) is
associated with the second occurrence of x(i).
The data value associated with the first appearance of a data site
is taken to be a function value; the data value associated with the
second appearance is taken to be a slope. If there were a third appearance
of that data site, the corresponding data value would be taken as
the second derivative value to be matched at that site. See Constructing and Working with B-form Splines for
a discussion of the command augknt used here to
generate the appropriate "knot sequence".
Smoothing
What if the data are noisy? For example, suppose that the given values are
noisy = y + .3*(rand(size(x))-.5);
Then you might prefer to approximate instead. For example, you might try the cubic smoothing spline, obtained by the command
scs = csaps(x,noisy);
and plotted by
fnplt(scs,2), hold on, plot(x,noisy,'o'),
legend('smoothing spline','noisy data'), hold off
This produces a figure like this:
Cubic Smoothing Spline of Noisy Data

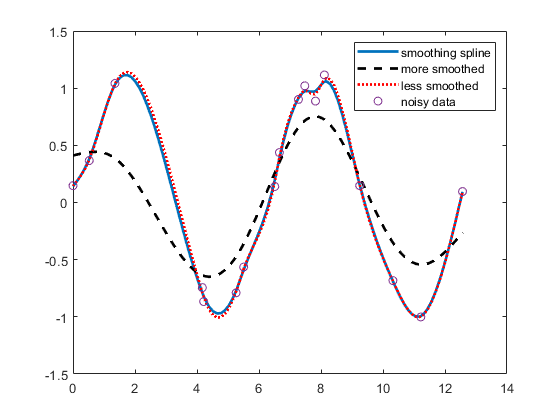
If you don't like the level of smoothing done by csaps(x,y),
you can change it by specifying the smoothing parameter, p,
as an optional third argument. Choose this number anywhere between
0 and 1. As p changes from 0 to 1, the smoothing
spline changes, correspondingly, from one extreme, the least squares
straight-line approximation to the data, to the other extreme, the
"natural" cubic spline interpolant to the data. Since csaps returns
the smoothing parameter actually used as an optional second output,
you could now experiment, as follows:
[scs,p] = csaps(x,noisy); fnplt(scs,2), hold on
fnplt(csaps(x,noisy,p/2),2,'k--'),
fnplt(csaps(x,noisy,(1+p)/2),2,'r:'), plot(x,noisy,'o')
legend('smoothing spline','more smoothed','less smoothed',...
'noisy data'), hold off
This produces the following picture.
Noisy Data More or Less Smoothed
At times, you might prefer simply to get the smoothest cubic
spline sp that is within a specified tolerance tol of
the given data in the sense that norm(noisy - fnval(sp,x))^2
<= tol. You create this spline with the command sp
= spaps(x,noisy,tol) for your defined tolerance tol.
Least Squares
If you prefer a least squares approximant, you can obtain it
by the statement sp = spap2(knots,k,x,y); in which
both the knot sequence knots and the order k of
the spline must be provided.
The popular choice for the order is 4, and that gives you a cubic spline. If you have no clear idea of how to choose the knots, simply specify the number of polynomial pieces you want used. For example,
sp = spap2(3,4,x,y);
gives a cubic spline consisting of three polynomial pieces.
If the resulting error is uneven, you might try for a better knot
distribution by using newknt as
follows:
sp = spap2(newknt(sp),4,x,y);