wdenoise
Wavelet signal denoising
Syntax
Description
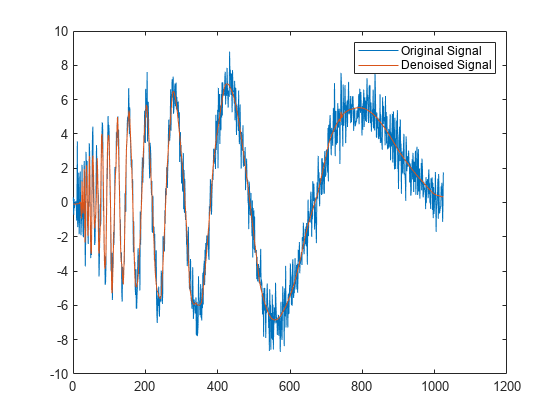
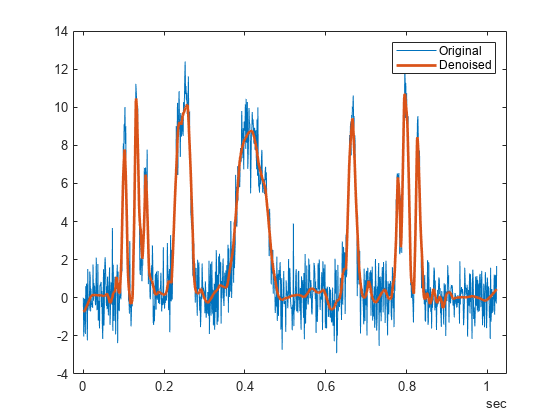
XDEN = wdenoise(X)X using an empirical Bayesian method
with a Cauchy prior. By default, the sym4 wavelet is used
with a posterior median threshold rule. Denoising is down to the minimum of
floor(log2N)
and wmaxlev(N,"sym4") where N is the
number of samples in the data. (For more information, see wmaxlev.)
X is a real-valued vector, matrix, or timetable.
If
Xis a matrix,wdenoisedenoises each column ofX.If
Xis a timetable,wdenoisemust contain real-valued vectors in separate variables, or one real-valued matrix of data.Xis assumed to be uniformly sampled.If
Xis a timetable and the timestamps are not linearly spaced,wdenoiseissues a warning.
XDEN = wdenoise(___,Name,Value)xden =
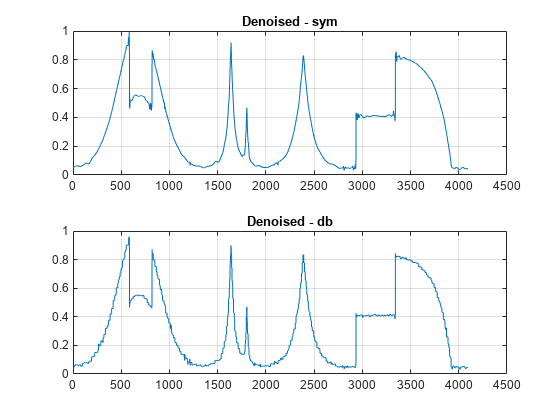
wdenoise(x,3,Wavelet="db2") denoises x down to
level 3 using the Daubechies db2 wavelet.
[
returns the denoised wavelet and scaling coefficients in the cell array
XDEN,DENOISEDCFS] = wdenoise(___)DENOISEDCFS. The elements of
DENOISEDCFS are in order of decreasing resolution. The
final element of DENOISEDCFS contains the approximation
(scaling) coefficients.
[
returns the original wavelet and scaling coefficients in the cell array
XDEN,DENOISEDCFS,ORIGCFS] = wdenoise(___)ORIGCFS. The elements of ORIGCFS
are in order of decreasing resolution. The final element of
ORIGCFS contains the approximation (scaling)
coefficients.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The most general model for the noisy signal has the following form:
where time n is equally spaced. In the simplest model, suppose that e(n) is a Gaussian white noise N(0,1), and the noise level σ is equal to 1. The denoising objective is to suppress the noise part of the signal s and to recover f.
The denoising procedure has three steps:
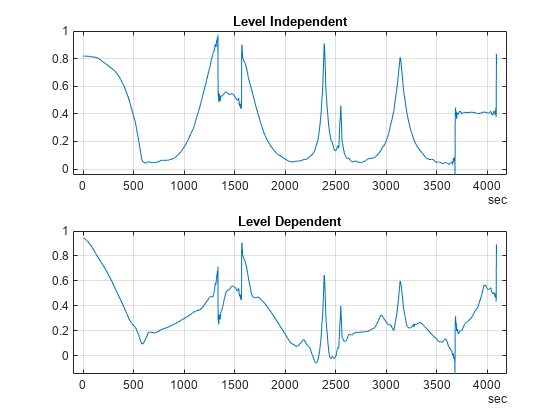
Decomposition — Choose a wavelet, and choose a level
N. Compute the wavelet decomposition of the signal s at levelN.Detail coefficients thresholding — For each level from 1 to
N, select a threshold and apply soft thresholding to the detail coefficients.Reconstruction — Compute wavelet reconstruction based on the original approximation coefficients of level
Nand the modified detail coefficients of levels from 1 toN.
More details about threshold selection rules are in Wavelet Denoising and Nonparametric Function Estimation and in the help of the thselect function.
References
[1] Abramovich, F., Y. Benjamini, D. L. Donoho, and I. M. Johnstone. “Adapting to Unknown Sparsity by Controlling the False Discovery Rate.” Annals of Statistics, Vol. 34, Number 2, pp. 584–653, 2006.
[2] Antoniadis, A., and G. Oppenheim, eds. Wavelets and Statistics. Lecture Notes in Statistics. New York: Springer Verlag, 1995.
[3] Cai, T. T. “On Block Thresholding in Wavelet Regression: Adaptivity, Block size, and Threshold Level.” Statistica Sinica, Vol. 12, pp. 1241–1273, 2002.
[4] Donoho, D. L. “Progress in Wavelet Analysis and WVD: A Ten Minute Tour.” Progress in Wavelet Analysis and Applications (Y. Meyer, and S. Roques, eds.). Gif-sur-Yvette: Editions Frontières, 1993.
[5] Donoho, D. L., I. M. Johnstone. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika, Vol. 81, pp. 425–455, 1994.
[6] Donoho, D. L. “De-noising by Soft-Thresholding.” IEEE Transactions on Information Theory, Vol. 42, Number 3, pp. 613–627, 1995.
[7] Donoho, D. L., I. M. Johnstone, G. Kerkyacharian, and D. Picard. “Wavelet Shrinkage: Asymptopia?” Journal of the Royal Statistical Society, series B, Vol. 57, No. 2, pp. 301–369, 1995.
[8] Johnstone, I. M., and B. W. Silverman. “Needles and Straw in Haystacks: Empirical Bayes Estimates of Possibly Sparse Sequences.” Annals of Statistics, Vol. 32, Number 4, pp. 1594–1649, 2004.
Extended Capabilities
Version History
Introduced in R2017b