rocmetrics
Receiver operating characteristic (ROC) curve and performance metrics for binary and multiclass classifiers
Since R2022a
Description
Create a rocmetrics object to evaluate the performance of a classification model using receiver operating characteristic (ROC) curves or other performance metrics. rocmetrics supports both binary and multiclass problems.
For each class, rocmetrics computes performance metrics for a one-versus-all ROC curve. You can compute metrics for an average ROC curve by
using the average function. After
computing metrics for ROC curves, you can plot them by using the plot function.
By default, rocmetrics computes the false positive rates (FPR) and the true
positive rates (TPR) to obtain a ROC curve. You can compute additional metrics by specifying
the AdditionalMetrics
name-value argument when you create an object or by calling the addMetrics function
after you create an object. A rocmetrics object stores the computed metrics
in the Metrics
properties.
In R2024b: You can find the area under the ROC curve (AUC) using the auc function.
rocmetrics computes pointwise confidence intervals for the performance
metrics when you set the NumBootstraps value to
a positive integer or when you specify cross-validated data for the true class labels
(Labels), classification
scores (Scores), and
observation weights (Weights). For details,
see Pointwise Confidence Intervals.
Creation
Syntax
Description
rocObj = rocmetrics(Labels,Scores,ClassNames)rocmetrics object using the true class labels in
Labels and the classification scores in
Scores. Specify Labels as a vector of length n,
and specify Scores as a matrix of size
n-by-K, where n is the number
of observations, and K is the number of classes.
ClassNames specifies the column order in
Scores.
The Metrics property
contains the performance metrics for each class for which you specify
Scores and ClassNames.
If you specify cross-validated data in Labels and
Scores as cell arrays, then rocmetrics computes
confidence intervals for the performance metrics.
rocObj = rocmetrics(Mdl,Tbl,ResponseVarName)rocmetrics object from a classification model object
Mdl, using the predictor data in Tbl with the
response variable name ResponseVarName as one column in
Tbl.
rocObj = rocmetrics(___,Name=Value)NumBootstraps=100 draws 100 bootstrap samples to compute
confidence intervals for the performance metrics.
Input Arguments
True class labels, specified as a numeric vector, logical vector, categorical vector, character array, string array, or cell array of character vectors. You can also specify Labels as a cell array of one of these types for cross-validated data.
For data that is not cross-validated, the length of
Labelsand the number of rows inScoresmust be equal.For cross-validated data, you must specify
Labels,Scores, andWeightsas cell arrays with the same number of elements.rocmetricstreats an element in the cell arrays as data from one cross-validation fold and computes pointwise confidence intervals for the performance metrics. The length ofLabels{i}and the number of rows inScores{i}must be equal.
Each row of Labels or Labels{i} represents the true label of one observation.
This argument sets the Labels
property.
Data Types: single | double | logical | char | string | cell
Classification scores, specified as a numeric matrix or a cell array of numeric matrices.
Each row of the matrix in Scores contains the classification scores of
one observation for all classes specified in ClassNames. The
column order of Scores must match the class order in
ClassNames.
For a matrix input,
Score(j,k)is the classification score of observationjfor classClassNames(k). You can specifyScoresby using the second output argument of thepredictfunction of a classification model object for both binary classification and multiclass classification. For example,predictofClassificationTreereturns classification scores as an n-by-K matrix, where n is the number of observations and K is the number classes. Pass the output torocmetrics.The number of rows in
Scoresand the length ofLabelsmust be equal.rocmetricsadjusts scores for each class relative to the scores for the rest of the classes. For details, see Adjusted Scores for Multiclass Classification Problem.For a vector input,
Score(j)is the classification score of observationjfor the class specified inClassNames.ClassNamesmust contain only one class.Priormust be a two-element vector withPrior(1)representing the prior probability for the specified class.Costmust be a2-by-2matrix containing[Cost(P|P),Cost(N|P);Cost(P|N),Cost(N|N)], wherePis a positive class (the class for which you specify classification scores), andNis a negative class.The length of
Scoresand the length ofLabelsmust be equal.
If you want to display the model operating point when you plot the ROC curve using the
plotfunction, the values inScore(j)must be the posterior probability. This restriction applies only to a vector input.For cross-validated data, you must specify
Labels,Scores, andWeightsas cell arrays with the same number of elements.rocmetricstreats an element in the cell arrays as data from one cross-validation fold and computes pointwise confidence intervals for the performance metrics.Score{i}(j,k)is the classification score of observationjin elementifor classClassNames(k). The number of rows inScores{i}and the length ofLabels{i}must be equal.
For more information, see Classification Score Input for rocmetrics.
This argument sets the Scores
property.
Data Types: single | double | cell
Class names, specified as a numeric vector, logical vector, categorical vector, character
array, string array, or cell array of character vectors. ClassNames
must have the same data type as the true labels in Labels. The values
in ClassNames must appear in Labels.
This argument sets the ClassNames
property.
Data Types: single | double | logical | cell | categorical
Since R2024b
Classification model, specified as a full or compact model object based on one of the following types:
For example, the following code creates a model object using the
fitctree function, and then passes the model object as an input
to the rocmetrics function.
Mdl = fitctree(X,Y); rocObj = rocmetrics(Mdl,X,Y);
Note
To create a rocmetrics object from a classification model, you must pass the training and response data as well as Mdl. For a cross-validated model, do not pass the training and response data.
Since R2024b
Sample data used for prediction, specified as a table. Each row of
Tbl corresponds to one observation, and each column corresponds
to one predictor variable. Tbl can contain one additional column
for the response variable. Multicolumn variables and cell arrays other than cell
arrays of character vectors are not allowed.
If
Tblcontains the response variable and you want to use all remaining variables as predictors, then specify the response variable usingResponseVarName.If
Tbldoes not contain the response variable, then specify the response data usingY. The length of the response variable and the number of rows ofTblmust be equal.
Data Types: table
Since R2024b
Response variable name, specified as the name of a variable in
Tbl. If Tbl contains the response variable
used to train Mdl, then you do not need to specify
ResponseVarName.
You must specify ResponseVarName as a character vector or
string scalar. For example, if the response variable Y is stored as
Tbl.Y, then specify it as "Y". Otherwise, the
software treats all columns of Tbl, including
Y, as predictors.
The response variable must be a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors. If the response variable is a character array, then each element must correspond to one row of the array.
Data Types: char | string
Since R2024b
Class labels, specified as a categorical, character, or string array, a logical or
numeric vector, or a cell array of character vectors. Y must have
the same data type as the response data used to train Mdl. (The software treats string arrays as cell arrays
of character vectors.)
The length of Y must equal the number of rows in
Tbl or X.
Data Types: categorical | char | string | logical | single | double | cell
Since R2024b
Predictor data, specified as a numeric matrix. Each row of X
represents one observation, and each column represents one variable.
Data Types: single | double
Since R2024b
Cross-validated classification model, specified as a model object based on one of the following types:
For example, the following code creates a cross-validated model using the
fitctree function, and then passes the model object as an input
to the rocmetrics function.
CVMdl = fitctree(X,Y,Crossval="on");
rocObj = rocmetrics(CVMdl);Note
To create a rocmetrics object from a classification model, you must pass the training and response data as well as Mdl. For a cross-validated model, do not pass the training and response data.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: rocObj =
rocmetrics(Labels,Scores,ClassNames,FixedMetric="FalsePositiveRate",FixedMetricValues=0:0.01:1)
holds the FPR values fixed at 0:0.01:1.
Performance Metrics
Additional model performance metrics to compute, specified as a character vector or string
scalar of the built-in metric name, string array of names, function handle
(@metricName), or cell array of names or function handles. A
rocmetrics object always computes the false positive rates (FPR) and
the true positive rates (TPR) to obtain a ROC curve. Therefore, you do not have to specify
to compute FPR and TPR.
Built-in metrics — Specify one of the following built-in metric names by using a character vector or string scalar. You can specify more than one by using a string array.
Name Description "TruePositives"or"tp"Number of true positives (TP) "FalseNegatives"or"fn"Number of false negatives (FN) "FalsePositives"or"fp"Number of false positives (FP) "TrueNegatives"or"tn"Number of true negatives (TN) "SumOfTrueAndFalsePositives"or"tp+fp"Sum of TP and FP "RateOfPositivePredictions"or"rpp"Rate of positive predictions (RPP), (TP+FP)/(TP+FN+FP+TN)"RateOfNegativePredictions"or"rnp"Rate of negative predictions (RNP), (TN+FN)/(TP+FN+FP+TN)"Accuracy"or"accu"Accuracy, (TP+TN)/(TP+FN+FP+TN)"FalseNegativeRate","fnr", or"miss"False negative rate (FNR), or miss rate, FN/(TP+FN)"TrueNegativeRate","tnr", or"spec"True negative rate (TNR), or specificity, TN/(TN+FP)"PositivePredictiveValue","ppv","prec", or"precision"Positive predictive value (PPV), or precision, TP/(TP+FP)"NegativePredictiveValue"or"npv"Negative predictive value (NPV), TN/(TN+FN)"ExpectedCost"or"ecost"Expected cost,
(TP*cost(P|P)+FN*cost(N|P)+FP*cost(P|N)+TN*cost(N|N))/(TP+FN+FP+TN), wherecostis a 2-by-2 misclassification cost matrix containing[0,cost(N|P);cost(P|N),0].cost(N|P)is the cost of misclassifying a positive class (P) as a negative class (N), andcost(P|N)is the cost of misclassifying a negative class as a positive class.The software converts the
K-by-Kmatrix specified by theCostname-value argument ofrocmetricsto a 2-by-2 matrix for each one-versus-all binary problem. For details, see Misclassification Cost Matrix."f1score"F1 score, 2*TP/(2*TP+FP+FN)You can obtain all of the previous metrics by specifying "all". You cannot specify"all"in conjunction with any other metric.The software computes the scale vector using the prior class probabilities (
Prior) and the number of classes inLabels, and then scales the performance metrics according to this scale vector. For details, see Performance Metrics.Custom metric — Specify a custom metric by using a function handle. A custom function that returns a performance metric must have this form:
metric = customMetric(C,scale,cost)
The output argument
metricis a scalar value.A custom metric is a function of the confusion matrix (
C), scale vector (scale), and cost matrix (cost). The software finds these input values for each one-versus-all binary problem. For details, see Performance Metrics.Cis a2-by-2confusion matrix consisting of[TP,FN;FP,TN].scaleis a2-by-1scale vector.costis a2-by-2misclassification cost matrix.
The software does not support cross-validation for a custom metric. Instead, you can specify to use bootstrap when you create a
rocmetricsobject.
Note that the positive predictive value (PPV) is
NaN for the reject-all threshold for which TP = FP = 0, and the negative predictive value (NPV) is NaN for the
accept-all threshold for which TN = FN = 0. For more details, see Thresholds, Fixed Metric, and Fixed Metric Values.
Example: AdditionalMetrics=["Accuracy","PositivePredictiveValue"]
Example: AdditionalMetrics={"Accuracy",@m1,@m2} specifies the
accuracy metric and the custom metrics m1 and
m2 as additional metrics. rocmetrics stores
the custom metric values as variables named CustomMetric1 and
CustomMetric2 in the Metrics
property.
Data Types: char | string | cell | function_handle
Fixed metric, specified as "Thresholds",
"FalsePositiveRate" (or "fpr"),
"TruePositiveRate" (or "tpr"), or a metric
specified by the AdditionalMetrics
name-value argument. To hold a custom metric fixed, specify
FixedMetric as "CustomMetricN", where
N is the number that refers to the custom metric. For example,
specify "CustomMetric1" to use the first custom metric specified by
AdditionalMetrics as the fixed metric.
rocmetrics finds the ROC curves and other metric values that correspond to
the fixed values (FixedMetricValues)
of the fixed metric (FixedMetric), and stores the values in the
Metrics property as
a table. For more details, see Thresholds, Fixed Metric, and Fixed Metric Values.
If rocmetrics computes confidence intervals, it uses one of two methods for
the computation, depending on the FixedMetric value:
If
FixedMetricis"Thresholds"(default),rocmetricsuses threshold averaging.If
FixedMetricis a nondefault value,rocmetricsuses vertical averaging.
For details, see Pointwise Confidence Intervals.
Example: FixedMetric="TruePositiveRate"
Data Types: char | string
Values for the fixed metric (FixedMetric),
specified as "all" or a numeric vector.
rocmetrics finds the ROC curves and other metric values that correspond to
the fixed values (FixedMetricValues) of the fixed metric
(FixedMetric), and stores the values in the Metrics property as
a table.
The default FixedMetric value is "Thresholds", and the
default FixedMetricValues value is "all". For
each class, rocmetrics uses all distinct adjusted score values as
threshold values and computes the performance metrics using the threshold values.
Depending on the UseNearestNeighbor
setting, rocmetrics uses the exact threshold values corresponding to
the fixed values or the nearest threshold values. For more details, see Thresholds, Fixed Metric, and Fixed Metric Values.
If rocmetrics computes confidence intervals, it holds FixedMetric fixed at FixedMetricValues.
FixedMetricvalue is"Thresholds", andFixedMetricValuesis"all"—rocmetricscomputes confidence intervals at the values corresponding to all distinct threshold values.FixedMetricvalue is a performance metric, andFixedMetricValuesis"all"—rocmetricsfinds the metric values corresponding to all distinct threshold values, and computes confidence intervals at the values corresponding to the metric values.
For details, see Pointwise Confidence Intervals.
Example: FixedMetricValues=0:0.01:1
Data Types: single | double
NaN condition, specified as "omitnan" or "includenan".
"omitnan"—rocmetricsignores allNaNscore values in the inputScoresand the corresponding values inLabelsandWeights."includenan"—rocmetricsuses theNaNscore values in the inputScoresfor the calculation. The function adds the observations withNaNscores to false classification counts in the respective class. That is, the function counts observations withNaNscores from the positive class as false negative (FN), and counts observations withNaNscores from the negative class as false positive (FP).
For more details, see NaN Score Values.
Example: NaNFlag="includenan"
Data Types: char | string
Indicator to use the nearest metric values, specified as a numeric or logical
0 (false) or 1
(true).
logical
0(false) —rocmetricsuses the exact threshold values corresponding to the specified fixed metric values inFixedMetricValuesforFixedMetric.logical
1(true) — Among the adjusted input scores,rocmetricsfinds a value that is the nearest to the threshold value corresponding to each specified fixed metric value.
For more details, see Thresholds, Fixed Metric, and Fixed Metric Values.
The UseNearestNeighbor value must be false if
rocmetrics computes confidence intervals. Otherwise, the default
value is true.
Example: UseNearestNeighbor=false
Data Types: single | double | logical
Options for Classification
Since R2024a
Flag to apply misclassification costs to scores for appropriate models, specified as a
numeric or logical 0 (false) or
1 (true). Set
ApplyCostToScores to true only when you
specify scores for a k-nearest neighbor (KNN), discriminant analysis,
or naive Bayes model with nondefault misclassification costs. These models use expected
classification costs rather than scores to predict labels.
If you specify ApplyCostToScores as true, the
software changes the scores to S*(-C), where the scores
S are specified by the Scores argument,
and the misclassification cost matrix C is specified by the Cost name-value
argument. The rocmetrics object stores the transformed scores in the
Scores property.
If you specify ApplyCostToScores as false, the
software stores the untransformed scores in the Scores property of
the rocmetrics object.
ApplyCostToScores does not apply to any
syntax that uses a model object as input.
Example: ApplyCostToScores=true
Data Types: single | double | logical
Misclassification cost, specified as a K-by-K square
matrix C, where K is the number of unique classes
in Labels.
C(i,j) is the cost of classifying a point into class
j if its true class is i (that is, the rows
correspond to the true class and the columns correspond to the predicted class).
ClassNames
specifies the order of the classes.
rocmetrics converts the K-by-K matrix
to a 2-by-2 matrix for each one-versus-all binary problem. For details, see Misclassification Cost Matrix.
If you specify classification scores for only one class in Scores, the
Cost value must be a
2-by-2 matrix containing
[0,cost(N|P);cost(P|N),0], where P is a
positive class (the class for which you specify classification scores), and
N is a negative class. cost(N|P) is the cost
of misclassifying a positive class as a negative class, and cost(P|N)
is the cost of misclassifying a negative class as a positive class.
The default value is C(i,j)=1 if i~=j, and C(i,j)=0 if i=j. The diagonal entries of a cost matrix must be zero.
Cost does not apply to any syntax that uses
a model object as input.
This argument sets the Cost
property.
Note
If you specify a misclassification cost
matrix when you use scores for a KNN, discriminant analysis, or naive Bayes model,
set ApplyCostToScores to
true. These models use expected classification costs rather
than scores to predict labels. (since R2024a)
Example: Cost=[0 2;1 0]
Data Types: single | double
Prior class probabilities, specified as one of the following:
"empirical"determines class probabilities from class frequencies in the true class labelsLabels. If you pass observation weights (Weights),rocmetricsalso uses the weights to compute the class probabilities."uniform"sets all class probabilities to be equal.Vector of scalar values, with one scalar value for each class.
ClassNamesspecifies the order of the classes.If you specify classification scores for only one class in
Scores, thePriorvalue must be a two-element vector withPrior(1)representing the prior probability for the specified class.
Prior does not apply to any syntax that
uses a model object as input.
This argument sets the Prior
property.
Example: Prior="uniform"
Data Types: single | double | char | string
Observation weights, specified as a numeric vector of positive values or a cell array containing numeric vectors of positive values.
For data that is not cross-validated, specify
Weightsas a numeric vector that has the same length asLabels.For cross-validated data, you must specify
Labels,Scores, andWeightsas cell arrays with the same number of elements.rocmetricstreats an element in the cell arrays as data from one cross-validation fold and computes pointwise confidence intervals for the performance metrics. The length ofWeights{i}and the length ofLabels{i}must be equal.
rocmetrics weighs the observations in Labels and
Scores with the corresponding values in
Weights. If you set the NumBootstraps value
to a positive integer, rocmetrics draws samples with replacement, using
the weights as multinomial sampling probabilities.
By default, Weights is a vector of ones or a cell array
containing vectors of ones.
You can
specify Weights for any syntax, including those that use a model
object as input.
This argument sets the Weights
property.
Data Types: single | double | cell
Options for Confidence Intervals
Significance level for the pointwise confidence intervals, specified as a scalar in the range (0,1).
If you specify Alpha as α, then
rocmetrics computes 100×(1 – α)% pointwise confidence intervals for the performance metrics.
This argument is related to computing confidence intervals. Therefore, it is valid only when
you specify cross-validated data for Labels, Scores, and
Weights, or when
you set the NumBootstraps value
to a positive integer.
Example: Alpha=0.01 specifies 99% confidence intervals.
Data Types: single | double
Bootstrap options for parallel computation, specified as a structure.
You can specify options for computing bootstrap iterations in parallel and setting random numbers during the bootstrap sampling. Create the BootstrapOptions structure with statset. This table lists the option fields and their values.
| Field Name | Field Value | Default |
|---|---|---|
UseParallel | Set this value to | false |
UseSubstreams | Set this value to To compute reproducibly, set | false |
Streams | Specify this value as a | If you do not specify |
This argument is valid only when you specify NumBootstraps as a
positive integer to compute confidence intervals using bootstrapping.
Parallel computation requires Parallel Computing Toolbox™.
Example: BootstrapOptions=statset(UseParallel=true)
Data Types: struct
Bootstrap confidence interval type, specified as one of the values in this table.
| Value | Description |
|---|---|
"bca" | Bias corrected and accelerated percentile method [11][12]. This method Involves a z0 factor computed using the proportion of bootstrap values that are less than the original sample value. To produce reasonable results when the sample is lumpy, the software computes z0 by including half of the bootstrap values that are the same as the original sample value. |
"corrected percentile" or
"cper" | Bias corrected percentile method [13] |
"normal" or "norm" | Normal approximated interval with bootstrapped bias and standard error [14] |
"percentile" or "per" | Basic percentile method |
"student" or "stud" | Studentized confidence interval [11] |
This argument is valid only when you specify NumBootstraps as a
positive integer to compute confidence intervals using bootstrapping.
Example: BootstrapType="student"
Data Types: char | string
Number of bootstrap samples to draw for computing pointwise confidence intervals, specified as a nonnegative integer scalar.
If you specify NumBootstraps as a positive integer, then
rocmetrics uses NumBootstraps bootstrap
samples. To create each bootstrap sample, the function randomly selects
n out of the n rows of input data with
replacement. The default value 0 implies that
rocmetrics does not use bootstrapping.
rocmetrics computes confidence intervals by using either
cross-validated data or bootstrap samples. Therefore, if you specify cross-validated
data for Labels, Scores, and
Weights, then
NumBootstraps must be 0.
For details, see Pointwise Confidence Intervals.
Example: NumBootstraps=500
Data Types: single | double
Number of bootstrap samples to draw for the studentized standard error estimate, specified as a positive integer scalar.
This argument is valid only when you specify NumBootstraps as a
positive integer and BootstrapType as
"student" to compute studentized bootstrap confidence intervals.
rocmetrics estimates the studentized standard error estimate by
using NumBootstrapsStudentizedSE bootstrap data samples.
Example: NumBootstrapsStudentizedSE=500
Data Types: single | double
Options for ECOC Models
Since R2024b
Binary learner loss function, specified as a built-in loss function name or function handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of passing a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function.
This table identifies the default BinaryLoss value, which depends on the
score ranges returned by the binary learners.
| Assumption | Default Value |
|---|---|
All binary learners are any of the following:
| "quadratic" |
| All binary learners are SVMs or linear or kernel classification models of SVM learners. | "hinge" |
All binary learners are ensembles trained by
AdaboostM1 or
GentleBoost. | "exponential" |
All binary learners are ensembles trained by
LogitBoost. | "binodeviance" |
You specify to predict class posterior probabilities by setting
FitPosterior=true in fitcecoc. | "quadratic" |
| Binary learners are heterogeneous and use different loss functions. | "hamming" |
To check the default value, use dot notation to display the BinaryLoss property of the trained model at the command line.
Example: BinaryLoss="binodeviance"
Data Types: char | string | function_handle
Decoding scheme that aggregates the binary losses, specified as
"lossweighted" or "lossbased". For more
information, see Binary Loss.
Example: Decoding="lossbased"
Data Types: char | string
Estimation options, specified as a structure array as returned by statset.
To invoke parallel computing you need a Parallel Computing Toolbox license.
Example: Options=statset(UseParallel=true)
Data Types: struct
Verbosity level, specified as 0 or 1.
Verbose controls the number of diagnostic messages that the
software displays in the Command Window.
If Verbose is 0, then the software does not display
diagnostic messages. Otherwise, the software displays diagnostic messages.
Example: Verbose=1
Data Types: single | double
Options for GAM Models
Since R2024b
Flag to include interaction terms of the model, specified as
true or false.
The default IncludeInteractions value is
true if the model contains interaction terms. The value must be
false if the model does not contain interaction terms.
Example: IncludeInteractions=false
Data Types: logical
Options for Ensembles
Since R2024b
Indices of the weak learners in the ensemble to use with
rocmetrics, specified as a
vector of positive integers in the range
[1:ens.NumTrained]. By default,
the function uses all learners.
Example: Learners=[1 2 4]
Data Types: single | double
Option to use observations for learners, specified as a logical matrix of size
N-by-T, where:
Nis the number of rows ofX.Tis the number of weak learners inens.
When UseObsForLearner(i,j) is true (default),
learner j is used in predicting the class of row i
of X.
Example: UseObsForLearner=logical([1 1; 0 1; 1 0])
Data Types: logical matrix
Flag to run in parallel, specified as a numeric or logical
1 (true) or 0
(false). If you specify UseParallel=true, the
rocmetrics function executes for-loop iterations by
using parfor. The loop runs in parallel when you
have Parallel Computing Toolbox.
Example: UseParallel=true
Data Types: logical
Options for Classification Trees
Since R2024b
Pruning level, specified as a vector of nonnegative integers in ascending order
or "all".
If you specify a vector, then all elements must be at least 0
and at most max(tree.PruneList). 0 indicates
the full, unpruned tree, and max(tree.PruneList) indicates the
completely pruned tree (that is, just the root node).
If you specify "all", then rocmetrics
operates on all subtrees (that is, the entire pruning sequence). This specification
is equivalent to using 0:max(tree.PruneList).
rocmetrics prunes tree to each level
specified by Subtrees, and then estimates the corresponding
output arguments. The size of Subtrees determines the size of
some output arguments.
For the function to invoke Subtrees, the properties
PruneList and PruneAlpha of
tree must be nonempty. In other words, grow
tree by setting Prune="on" when you use
fitctree, or by pruning tree using prune.
Example: Subtrees="all"
Data Types: single | double | char | string
Options for Neural Network ECOC Classification Models
Since R2024b
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a
table.
Example: ObservationsIn="columns"
Data Types: char | string
Options for Cross-Validated Models
Since R2024b
Confidence interval type, specified as one of the following:
"crossval"— Create confidence intervals using the cross-validation folds."bootstrap"— Create confidence intervals using bootstrapping. In this case, the defaultNumBootstrapsis100."none"— Do not create confidence intervals.
Example: ConfidenceIntervalType="bootstrap"
Data Types: char | string
Indication to include interactions in the prediction, specified as
false or true. The default value is
true if the model has interactions, and
false otherwise. This argument applies only to a ClassificationPartitionedGAM model or a non-cross-validated ClassificationGAM model.
Example: IncludeInteractions=false
Data Types: logical
Properties
Performance Metrics
This property is read-only.
Performance metrics, specified as a table.
The table contains performance metric values for all classes, vertically concatenated
according to the class order in ClassNames. The
table has a row for each unique threshold value for each class.
rocmetrics determines the threshold values to use based on the
value of FixedMetric,
FixedMetricValues,
and UseNearestNeighbor.
For details, see Thresholds, Fixed Metric, and Fixed Metric Values.
The number of rows for each class in the table is the number of unique threshold values.
Each row of the table contains these variables: ClassName,
Threshold, FalsePositiveRate, and
TruePositiveRate, as well as a variable for each additional
metric specified in AdditionalMetrics.
If you specify a custom metric, rocmetrics names the metric
"CustomMetricN", where N is the number that
refers to the custom metric. For example, "CustomMetric1" corresponds
to the first custom metric specified by AdditionalMetrics.
Each variable in the Metrics table contains a vector or a three-column matrix.
If
rocmetricsdoes not compute confidence intervals, each variable contains a vector.If
rocmetricscomputes confidence intervals, bothClassNameand the variable forFixedMetric(Threshold,FalsePositiveRate,TruePositiveRate, or an additional metric) contain a vector, and the other variables contain a three-column matrix. The first column of the matrix corresponds to the metric values, and the second and third columns correspond to the lower and upper bounds, respectively.
Data Types: table
Classification Model Properties
You can specify the following properties when creating a rocmetrics
object.
This property is read-only.
Class names, specified as a numeric vector, logical vector, categorical vector, or cell array of character vectors.
For details, see the input argument ClassNames, which
sets this property. (The software treats character or string arrays as cell arrays of character vectors.)
Data Types: single | double | logical | cell | categorical
This property is read-only.
Misclassification cost, specified as a square matrix.
For details, see the Cost name-value
argument, which sets this property.
Data Types: single | double
This property is read-only.
True class labels, specified as a numeric vector, logical vector, categorical vector, cell array of character vectors, or cell array of one of these types for cross-validated data.
For details, see the input argument Labels, which sets
this property. (The software treats character or string arrays as cell arrays of character vectors.)
Data Types: single | double | logical | cell | categorical
This property is read-only.
Prior class probabilities, specified as a numeric vector.
For details, see the Prior name-value
argument, which sets this property. If you specify this argument as a character vector
or string scalar ("empirical" or "uniform"),
rocmetrics computes the prior probabilities and stores the
Prior property as a numeric vector.
Data Types: single | double
This property is read-only.
Classification scores, specified as a numeric matrix or a cell array of numeric matrices.
For details, see the input argument Scores, which sets
this property.
Note
If you specify the ApplyCostToScores
name-value argument as true, the software stores the transformed
scores S*(-C), where the scores S are
specified by the Scores argument, and the misclassification
cost matrix C is specified by the Cost name-value
argument. (since R2024a)
Data Types: single | double | cell
This property is read-only.
Observation weights, specified as a numeric vector of positive values or a cell array containing numeric vectors of positive values.
For details, see the Weights name-value
argument, which sets this property.
Data Types: single | double | cell
Object Functions
addMetrics | Compute additional classification performance metrics |
auc | Area under ROC curve or precision-recall curve |
average | Compute performance metrics for average receiver operating characteristic (ROC) curve in multiclass problem |
modelOperatingPoint | Operating point of rocmetrics object |
plot | Plot receiver operating characteristic (ROC) curves and other performance curves |
Examples
Compute the performance metrics (FPR and TPR) for a binary classification problem by creating a rocmetrics object, and plot a ROC curve by using the plot function.
Load the ionosphere data set. This data set has 34 predictors (X) and 351 binary responses (Y) for radar returns, either bad ('b') or good ('g').
load ionospherePartition the data into training and test sets. Use approximately 80% of the observations to train a support vector machine (SVM) model, and 20% of the observations to test the performance of the trained model on new data. Partition the data using cvpartition.
rng("default") % For reproducibility of the partition c = cvpartition(Y,Holdout=0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set XTrain = X(trainingIndices,:); YTrain = Y(trainingIndices); XTest = X(testIndices,:); YTest = Y(testIndices);
Train an SVM classification model.
Mdl = fitcsvm(XTrain,YTrain);
Compute the classification scores for the test set.
[~,Scores] = predict(Mdl,XTest); size(Scores)
ans = 1×2
70 2
The output Scores is a matrix of size 70-by-2. The column order of Scores follows the class order in Mdl. Display the class order stored in Mdl.ClassNames.
Mdl.ClassNames
ans = 2×1 cell
{'b'}
{'g'}
Create a rocmetrics object by using the true labels in YTest and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames.
rocObj = rocmetrics(YTest,Scores,Mdl.ClassNames);
rocObj is a rocmetrics object that stores the performance metrics for each class in the Metrics property. Compute the AUC values using the auc function.
a = auc(rocObj)
a = 1×2
0.8587 0.8587
For a binary classification problem, the AUC values are equal to each other.
The table in Metrics contains the performance metric values for both classes, vertically concatenated according to the class order. Find the rows for the first class in the table, and display the first eight rows.
idx = strcmp(rocObj.Metrics.ClassName,Mdl.ClassNames(1)); head(rocObj.Metrics(idx,:))
ClassName Threshold FalsePositiveRate TruePositiveRate
_________ _________ _________________ ________________
{'b'} 15.545 0 0
{'b'} 15.545 0 0.04
{'b'} 15.105 0 0.08
{'b'} 11.424 0 0.16
{'b'} 10.077 0 0.2
{'b'} 9.9716 0 0.24
{'b'} 9.9417 0 0.28
{'b'} 9.0338 0 0.32
Plot the ROC curve for each class by using the plot function.
plot(rocObj)

For each class, the plot function plots a ROC curve and displays a filled circle marker at the model operating point. The legend displays the class name and AUC value for each curve.
Note that you do not need to examine ROC curves for both classes in a binary classification problem. The two ROC curves are symmetric, and the AUC values are identical. A TPR of one class is a true negative rate (TNR) of the other class, and TNR is 1-FPR. Therefore, a plot of TPR versus FPR for one class is the same as a plot of 1-FPR versus 1-TPR for the other class.
Plot the ROC curve for the first class only by specifying the ClassNames name-value argument.
plot(rocObj,ClassNames=Mdl.ClassNames(1))

Compute the performance metrics (FPR and TPR) for a multiclass classification problem by creating a rocmetrics object, and plot a ROC curve for each class by using the plot function. Specify the AverageCurveType name-value argument of plot to create the average ROC curve for the multiclass problem.
Load the fisheriris data set. The matrix meas contains flower measurements for 150 different flowers. The vector species lists the species for each flower. species contains three distinct flower names.
load fisheririsTrain a classification tree that classifies observations into one of the three labels. Cross-validate the model using 10-fold cross-validation.
rng("default") % For reproducibility Mdl = fitctree(meas,species,Crossval="on");
Compute the classification scores for validation-fold observations.
[~,Scores] = kfoldPredict(Mdl); size(Scores)
ans = 1×2
150 3
The output Scores is a matrix of size 150-by-3. The column order of Scores follows the class order in Mdl. Display the class order stored in Mdl.ClassNames.
Mdl.ClassNames
ans = 3×1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
Create a rocmetrics object by using the true labels in species and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames.
rocObj = rocmetrics(species,Scores,Mdl.ClassNames);
rocObj is a rocmetrics object that stores the performance metrics for each class in the Metrics property. Compute the AUC values by using the auc function.
a = auc(rocObj)
a = 1×3
1.0000 0.9636 0.9636
The table in Metrics contains the performance metric values for all three classes, vertically concatenated according to the class order. Find and display the rows for the second class in the table.
idx = strcmp(rocObj.Metrics.ClassName,Mdl.ClassNames(2)); rocObj.Metrics(idx,:)
ans=13×4 table
ClassName Threshold FalsePositiveRate TruePositiveRate
______________ _________ _________________ ________________
{'versicolor'} 1 0 0
{'versicolor'} 1 0.01 0.7
{'versicolor'} 0.95455 0.02 0.8
{'versicolor'} 0.91304 0.03 0.9
{'versicolor'} -0.2 0.04 0.9
{'versicolor'} -0.33333 0.06 0.9
{'versicolor'} -0.6 0.08 0.9
{'versicolor'} -0.86957 0.12 0.92
{'versicolor'} -0.91111 0.16 0.96
{'versicolor'} -0.95122 0.31 0.96
{'versicolor'} -0.95238 0.38 0.98
{'versicolor'} -0.95349 0.44 0.98
{'versicolor'} -1 1 1
Plot the ROC curve for each class. Specify AverageCurveType="micro" to compute the performance metrics for the average ROC curve using the micro-averaging method.
plot(rocObj,AverageCurveType="micro")
Load the ionosphere data into your workspace.
load ionosphere
whoYour variables are: Description X Y
The data is in variable X and the response is in variable Y. Create a classification tree model of the data.
Mdl = fitctree(X,Y);
Create rocmetrics Object from Model and Matrix Data
Create a rocmetrics object from the classification tree model, using X and Y as the predictor data and response data.
rocMdl = rocmetrics(Mdl,X,Y);
Plot the ROC curve for the rocmetrics object.
plot(rocMdl)
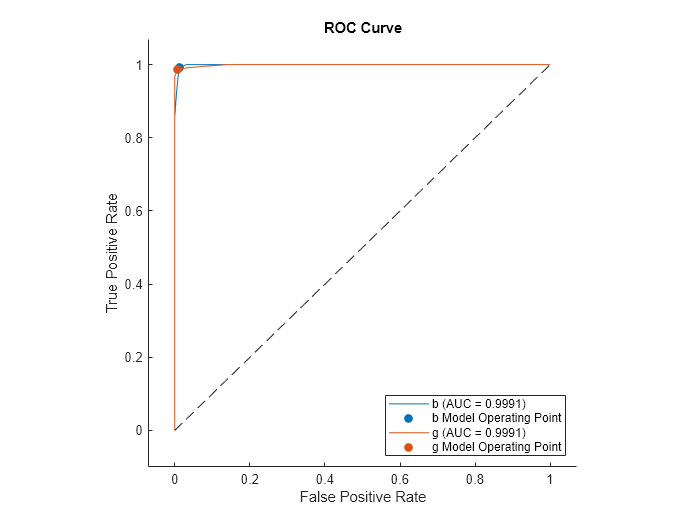
Create rocmetrics Object from Model and Table Data
Create a table of the X data.
save("datafile.txt","X","-ascii"); Tbl = readtable("datafile.txt");
Create a rocmetrics object from the classification tree model, using Tbl as the predictor data and Y as the response data.
Mdl2 = fitctree(Tbl,Y); rocMdl2 = rocmetrics(Mdl2,Tbl,Y);
Plot the ROC curve for rocMdl2. The plot is the same as the previous one.
plot(rocMdl2)
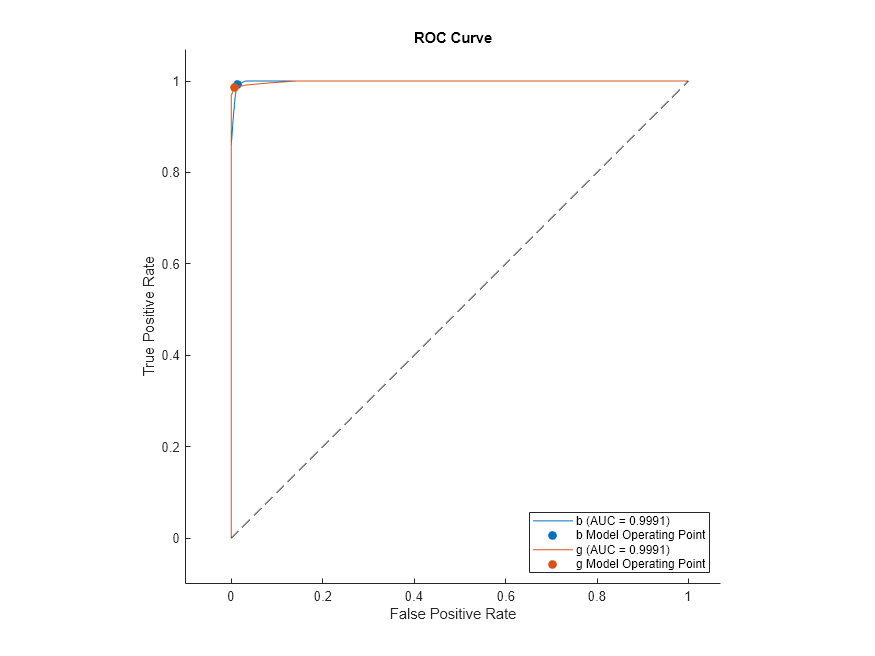
Create rocmetrics Object from Model and Table with Response
Place the response data Y into Tbl with the variable name Resp.
Tbl.Resp = Y;
Create a rocmetrics object from Tbl specifying Resp as the response variable name.
Mdl3 = fitctree(Tbl,"Resp"); rocMdl3 = rocmetrics(Mdl3,Tbl,"Resp");
Plot the ROC curve for rocMdl3. The plot is the same as the previous ones.
plot(rocMdl3)
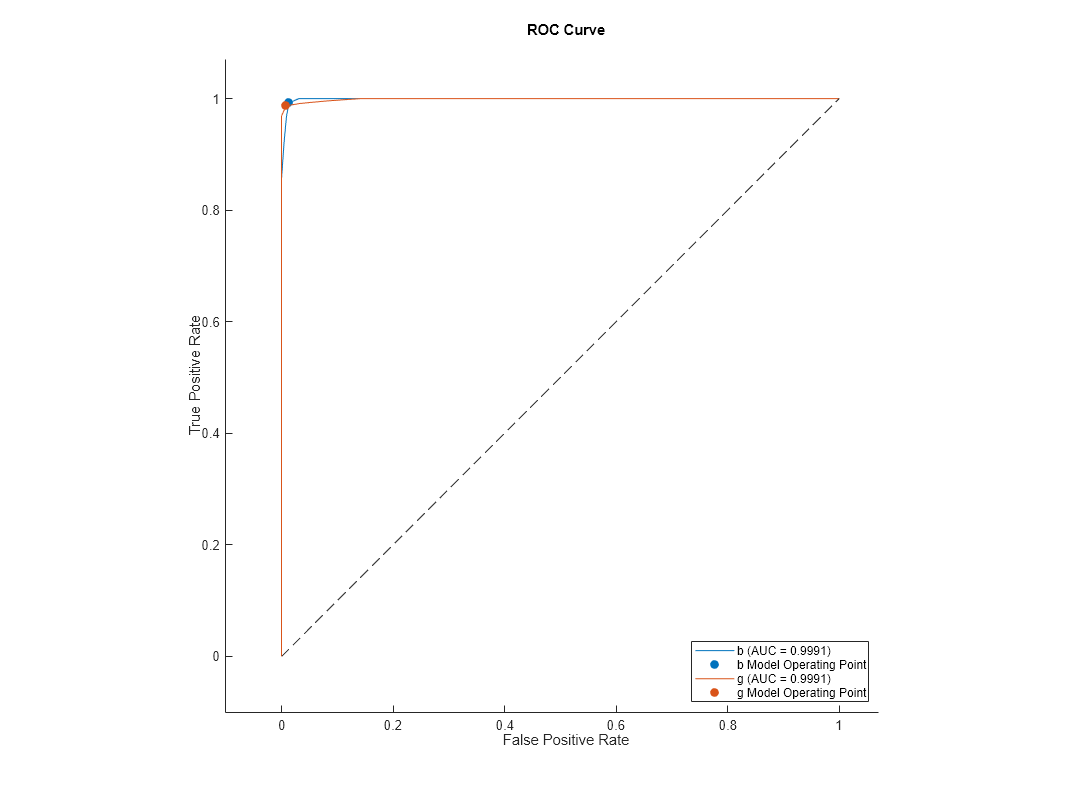
Create rocmetrics Object from Cross-Validated Model
Create a cross-validated classification tree model.
rng default % For reproducibility CVMdl = fitctree(X,Y,KFold=5);
Create a rocmetrics object from the cross-validated model.
rocMdl4 = rocmetrics(CVMdl);
Plot the ROC curve for rocMdl4.
plot(rocMdl4)
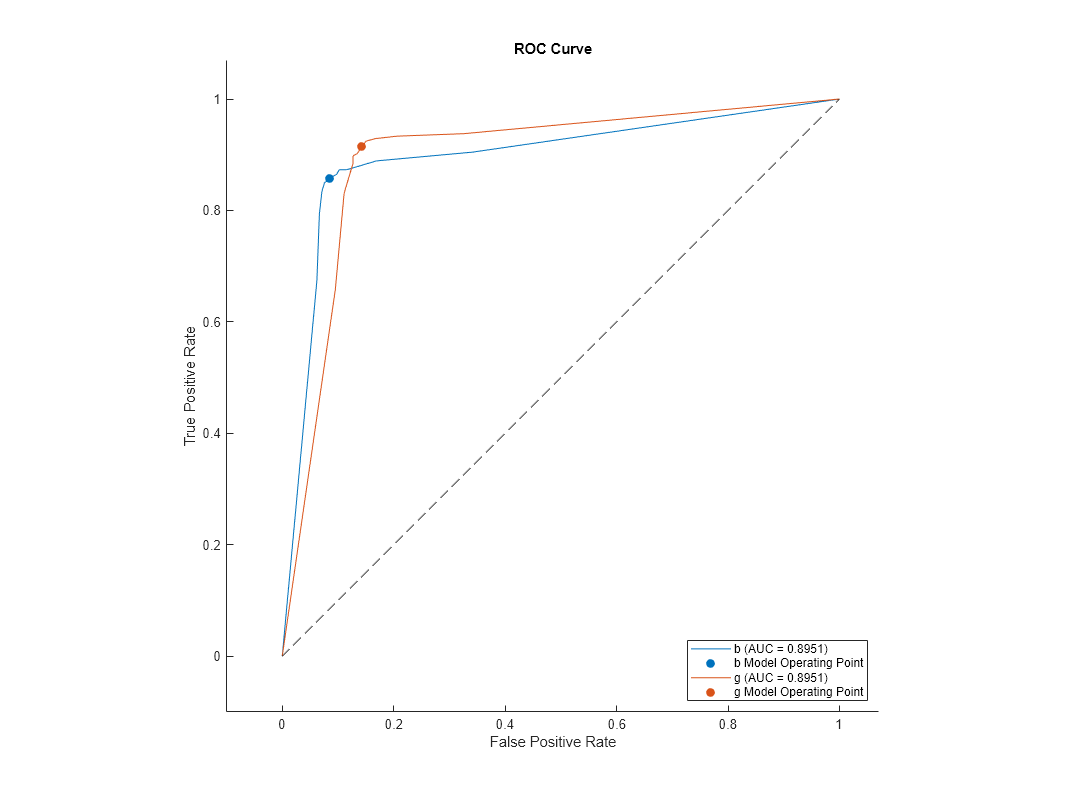
This ROC curve looks different than the previous ones. The cross-validated model has more realistic ROC curves.
k-nearest neighbor (KNN), discriminant analysis, and naive Bayes classifiers use expected classification costs rather than scores to predict labels. When you want to use nondefault misclassification costs to create ROC curves for these models, set the ApplyCostToScores name-value argument of the rocmetrics function to true.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency.
creditrating = readtable("CreditRating_Historical.dat");Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table.
creditrating = removevars(creditrating,"ID");Combine all the A ratings into one rating. Do the same for the B and C ratings, so that the response variable has three distinct ratings. Among the three ratings, A is considered the best and C the worst.
Rating = categorical(creditrating.Rating); Rating = mergecats(Rating,["AAA","AA","A"],"A"); Rating = mergecats(Rating,["BBB","BB","B"],"B"); Rating = mergecats(Rating,["CCC","CC","C"],"C"); creditrating.Rating = Rating;
Assume that specific costs are associated with misclassifying the credit ratings of customers. Create a matrix variable that contains the misclassification costs. Create another variable that specifies the class names and their order in the matrix variable.
classificationCosts = [0 100 200; 500 0 100; 1000 500 0]; classNames = categorical(["A","B","C"]);
The costs indicate that classifying a customer with bad credit as a customer with good credit is more costly than classifying a customer with good credit as a customer with bad credit. For example, the cost of misclassifying a C rating customer as an A rating customer is $1000.
Partition the data into training and test sets. Use 75% of the observations to train a discriminant analysis classifier, and 25% of the observations to test the performance of the trained model on new data.
rng("default") % For reproducibility c = cvpartition(creditrating.Rating,"Holdout",0.25); trainRatings = creditrating(training(c),:); testRatings = creditrating(test(c),:);
Train a discriminant analysis classifier. Specify the misclassification costs.
mdl = fitcdiscr(trainRatings,"Rating",Cost=classificationCosts, ... ClassNames=classNames);
Predict the class labels, scores, and expected classification costs for the observations in the test set.
[labels,scores,expectedCosts] = predict(mdl,testRatings);
For each observation, the predicted class label corresponds to the minimum expected classification cost among all classes rather than the greatest score (or posterior probability).
For example, display the predictions for the first observation in the test set.
firstLabel = labels(1)
firstLabel = categorical
B
firstScores = array2table(scores(1,:),VariableNames=["A","B","C"])
firstScores=1×3 table
A B C
_______ _______ __________
0.70807 0.29193 4.7141e-13
firstExpectedCosts = array2table(expectedCosts(1,:), ... VariableNames=["A","B","C"])
firstExpectedCosts=1×3 table
A B C
______ ______ ______
145.96 70.807 170.81
The predicted label corresponds to class B, which has the lowest expected classification cost, even though class A has the greatest posterior probability.
Create a rocmetrics object by using the true labels in testRatings and the classification scores in scores. Specify the column order of scores. To use nondefault misclassification costs and scores returned by a discriminant analysis model, specify the Cost and ApplyCostToScores name-value arguments.
roc = rocmetrics(testRatings.Rating,scores,classNames, ...
Cost=classificationCosts,ApplyCostToScores=true);Notice that the scores stored in rocmetrics are the negative expected classification costs.
isequal(roc.Scores,-expectedCosts)
ans = logical
1
Plot the ROC curve for each class by using the plot function.
plot(roc,ClassNames=classNames)

For each class, the plot function plots a curve. The filled circle markers indicate the model operating points.
Train a cross-validated discriminant analysis classifier by using the entire creditrating data set.
cvmdl = fitcdiscr(creditrating,"Rating",Cost=classificationCosts, ... ClassNames=classNames,CrossVal="on")
cvmdl =
ClassificationPartitionedModel
CrossValidatedModel: 'Discriminant'
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
NumObservations: 3932
KFold: 10
Partition: [1×1 cvpartition]
ClassNames: [A B C]
ScoreTransform: 'none'
Properties, Methods
The fitcdiscr function creates a ClassificationPartitionedModel object of type Discriminant (CrossValidatedModel property value). To create the cross-validated model, the function completes these steps:
Randomly partition the data into 10 sets.
For each set, reserve the set as validation data, and train the model using the other 9 sets.
Store the 10 compact trained models in a 10-by-1 cell vector in the
Trainedproperty of the cross-validated model object.
cvmdl.Trained
ans=10×1 cell array
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
{1×1 classreg.learning.classif.CompactClassificationDiscriminant}
Predict the class label, scores, and expected classification costs for each observation.
[cvlabels,cvscores,cvexpectedCosts] = kfoldPredict(cvmdl);
Plot the ROC curve for each class.
cvroc = rocmetrics(creditrating.Rating,cvscores,classNames, ...
Cost=classificationCosts,ApplyCostToScores=true);
plot(cvroc,ClassNames=classNames)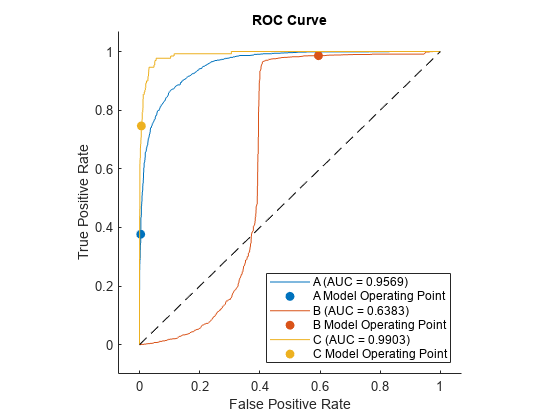
The cross-validation results are similar to the previous test set results.
For generated samples containing outliers, train an isolation forest model and compute anomaly scores by using the iforest function. iforest returns scores as a vector. Use the scores to create a rocmetrics object. Plot the precision-recall curve using the anomaly scores, and find the model operating point for the isolation forest model.
Use a Gaussian copula to generate random data points from a bivariate distribution.
rng("default") rho = [1,0.05;0.05,1]; n = 1000; u = copularnd("Gaussian",rho,n);
Add noise to 5% of randomly selected observations to make the observations outliers.
noise = randperm(n,0.05*n); true_tf = false(n,1); true_tf(noise) = true; u(true_tf,1) = u(true_tf,1)*5;
Train an isolation forest model by using the iforest function. Specify the fraction of anomalies in the training observations as 0.05.
[f,tf,scores] = iforest(u,ContaminationFraction=0.05);
f is an IsolationForest object. iforest also returns the anomaly indicators (tf) and anomaly scores (scores) for the training data. iforest determines the threshold value (f.ScoreThreshold) so that the function detects the specified fraction of training observations as anomalies.
Check the performance of the IsolationForest object by plotting the precision-recall curve, which computes the area under the curve (AUC) value. Create a rocmetrics object by using the true anomaly indicators (true_tf) and anomaly scores (scores). A score value close to 1 indicates an anomaly, as does the value true in true_tf. Therefore, specify the class name for scores as true. Specify the AdditionalMetrics name-value argument to compute the precision values (or positive predictive values).
rocObj = rocmetrics(true_tf,scores,true,AdditionalMetrics="PositivePredictiveValue");Plot the curve by using the plot function of rocmetrics. Specify the y-axis metric as precision (or positive predictive value) and the x-axis metric as recall (or true positive rate). Display a filled circle at the model operating point corresponding to f.ScoreThreshold.
r = plot(rocObj,YAxisMetric="PositivePredictiveValue",XAxisMetric="TruePositiveRate",... ShowModelOperatingPoint=true);

Compute the confidence intervals for FPR and TPR for fixed threshold values by using bootstrap samples, and plot the confidence intervals for TPR on the ROC curve by using the plot function.
Load the ionosphere data set. This data set has 34 predictors (X) and 351 binary responses (Y) for radar returns, either bad ('b') or good ('g').
load ionospherePartition the data into training and test sets. Use approximately 80% of the observations to train a support vector machine (SVM) model, and 20% of the observations to test the performance of the trained model on new data. Partition the data using cvpartition.
rng("default") % For reproducibility of the partition c = cvpartition(Y,Holdout=0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set XTrain = X(trainingIndices,:); YTrain = Y(trainingIndices); XTest = X(testIndices,:); YTest = Y(testIndices);
Train an SVM classification model.
Mdl = fitcsvm(XTrain,YTrain);
Compute the classification scores for the test set.
[~,Scores] = predict(Mdl,XTest);
Create a rocmetrics object by using the true labels in YTest and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames. Specify NumBootstraps as 100 to use 100 bootstrap samples to compute the confidence intervals.
rocObj = rocmetrics(YTest,Scores,Mdl.ClassNames, ...
NumBootstraps=100);Find the rows for the second class in the table of the Metrics property, and display the first eight rows.
idx = strcmp(rocObj.Metrics.ClassName,Mdl.ClassNames(2)); head(rocObj.Metrics(idx,:))
ClassName Threshold FalsePositiveRate TruePositiveRate
_________ _________ __________________________ ________________________________
{'g'} 7.1963 0 0 0 0 0 0
{'g'} 7.1963 0 0 0 0.022222 0 0.093023
{'g'} 6.2593 0 0 0 0.044444 0 0.11969
{'g'} 5.5728 0 0 0 0.066667 0.020988 0.16024
{'g'} 5.5642 0 0 0 0.088889 0.022635 0.18805
{'g'} 5.4619 0.04 0 0.22222 0.088889 0.022635 0.18805
{'g'} 5.3672 0.08 0 0.28 0.088889 0.022635 0.18805
{'g'} 5.1525 0.08 0 0.28 0.11111 0.045035 0.19532
Each row of the table contains the metric value and its confidence intervals for FPR and TPR for a fixed threshold value. The Threshold variable is a column vector, and the FalsePositiveRate and TruePositiveRate variables are three-column matrices. The first column of the matrices corresponds to the metric values, and the second and third columns correspond to the lower and upper bounds, respectively.
Plot the ROC curve and the confidence intervals for TPR. Specify ShowConfidenceIntervals=true to show the confidence intervals, and specify one class to plot by using the ClassNames name-value argument.
plot(rocObj,ShowConfidenceIntervals=true,ClassNames=Mdl.ClassNames(2))
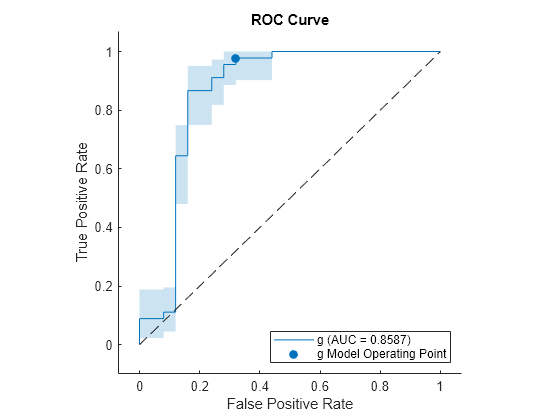
The shaded area around the ROC curve indicates the confidence intervals. The confidence intervals represent the uncertainty of the curve due to the variance in the test set for the trained model.
Compute the confidence intervals for FPR and TPR for fixed threshold values by using cross-validated data, and plot the confidence intervals for TPR on the ROC curve by using the plot function.
Load the fisheriris data set. The matrix meas contains flower measurements for 150 different flowers. The vector species lists the species for each flower. species contains three distinct flower names.
load fisheririsTrain a naive Bayes model that classifies observations into one of the three labels. Cross-validate the model using 10-fold cross-validation.
rng("default") % For reproducibility Mdl = fitcnb(meas,species,Crossval="on");
Compute the classification scores for validation-fold observations.
[~,Scores] = kfoldPredict(Mdl);
Store the cross-validated scores and the corresponding true labels in cell arrays, so that each element in the cell arrays corresponds to one validation fold.
cv = Mdl.Partition; numTestSets = cv.NumTestSets; cvLabels = cell(numTestSets,1); cvScores = cell(numTestSets,1); for i = 1:numTestSets testIdx = test(cv,i); cvLabels{i} = species(testIdx); cvScores{i} = Scores(testIdx,:); end
Create a rocmetrics object using the cell arrays. If you specify true labels and scores by using cell arrays, rocmetrics computes the confidence intervals.
rocObj = rocmetrics(cvLabels,cvScores,Mdl.ClassNames);
Plot the ROC curve and the confidence intervals for TPR. Specify ShowConfidenceIntervals=true to show the confidence intervals.
plot(rocObj,ShowConfidenceIntervals=true)
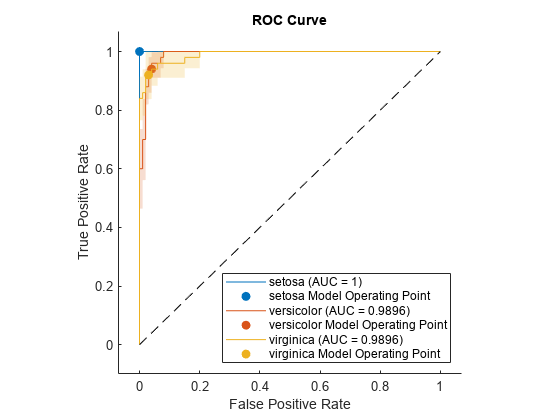
The shaded area around each curve indicates the confidence intervals. The widths of the confidence intervals for setosa are 0 for nonzero false positive rates, so the plot does not have a shaded area for setosa. The confidence intervals reflect the uncertainty in the model due to the variance in the training and test sets.
Train three different classification models: decision tree model, generalized additive model, and naive Bayes model. Compare the performance of the three models on a test data set using the ROC curves and the AUC values.
Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year.
load census1994census1994 contains the training data set adultdata and the test data set adulttest. Display the unique values in the response variable salary.
classNames = unique(adultdata.salary)
classNames = 2×1 categorical
<=50K
>50K
Train the three models by passing the training data adultdata and specifying the response variable name "salary". Specify the order of the classes by using the ClassNames name-value argument.
MdlTree = fitctree(adultdata,"salary",ClassNames=classNames); MdlGAM = fitcgam(adultdata,"salary",ClassNames=classNames); MdlNB = fitcnb(adultdata,"salary",ClassNames=classNames);
Compute the classification scores for the test data set adulttest using the trained models.
[~,ScoresTree] = predict(MdlTree,adulttest); [~,ScoresGAM] = predict(MdlGAM,adulttest); [~,ScoresNB] = predict(MdlNB,adulttest);
Create a rocmetrics object for each model.
rocTree = rocmetrics(adulttest.salary,ScoresTree,classNames); rocGAM = rocmetrics(adulttest.salary,ScoresGAM,classNames); rocNB = rocmetrics(adulttest.salary,ScoresNB,classNames);
Plot the ROC curve for each model. By default, the plot function displays the class names and the AUC values in the legend. To include the model names in the legend instead of the class names, modify the DisplayName property of the ROCCurve object returned by the plot function.
figure
c = cell(3,1);
g = cell(3,1);
[c{1},g{1}] = plot(rocTree,ClassNames=classNames(1));
hold on
[c{2},g{2}] = plot(rocGAM,ClassNames=classNames(1));
[c{3},g{3}] = plot(rocNB,ClassNames=classNames(1));
modelNames = ["Decision Tree Model", ...
"Generalized Additive Model","Naive Bayes Model"];
for i = 1 : 3
c{i}.DisplayName = replace(c{i}.DisplayName, ...
string(classNames(1)),modelNames(i));
g{i}(1).DisplayName = join([modelNames(i),"Operating Point"]);
end
hold off
The generalized additive model (MdlGAM) has the highest AUC value, and the decision tree model (MdlTree) has the lowest. This result suggests that MdlGAM has better average performance for the test data set than MdlTree and MdlNB.
Find the model operating point and the optimal operating point for a binary classification model. Classify observations in a test data set by using a new threshold corresponding to the optimal operating point.
Load the ionosphere data set. This data set has 34 predictors (X) and 351 binary responses (Y) for radar returns, either bad (b) or good (g).
load ionospherePartition the data into training and test sets. Use approximately 75% of the observations to train a support vector machine (SVM) model, and 25% of the observations to test the performance of the trained model on new data. Partition the data using cvpartition.
rng("default") % For reproducibility of the partition c = cvpartition(Y,Holdout=0.25); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set XTrain = X(trainingIndices,:); YTrain = Y(trainingIndices); XTest = X(testIndices,:); YTest = Y(testIndices);
Train an SVM classification model.
Mdl = fitcsvm(XTrain,YTrain);
Display the class order stored in Mdl.ClassNames.
Mdl.ClassNames
ans = 2×1 cell
{'b'}
{'g'}
Compute the classification scores for the test set.
[Y1,Scores] = predict(Mdl,XTest);
Create a rocmetrics object by using the true labels in YTest and the classification scores in Scores. Specify the column order of Scores using Mdl.ClassNames.
rocObj = rocmetrics(YTest,Scores,Mdl.ClassNames);
Find the model operating point by using the modelOperatingPoint function.
modelpt = modelOperatingPoint(rocObj)
modelpt=2×4 table
ClassName Threshold FalsePositiveRate TruePositiveRate
_________ _________ _________________ ________________
{'b'} 1.2654 0.017857 0.58065
{'g'} 0.21911 0.41935 0.98214
How does this function work? The predict function classifies an observation into the class yielding a larger score, which corresponds to the class with a nonnegative adjusted score. That is, the typical threshold value used by the predict function is 0. Among the rows in the Metrics property of rocObj for class b, find the point that has the smallest nonnegative threshold value. The point on the curve indicates identical performance to the performance of the threshold value 0.
idx_b = strcmp(rocObj.Metrics.ClassName,"b"); X = rocObj.Metrics(idx_b,:).FalsePositiveRate; Y = rocObj.Metrics(idx_b,:).TruePositiveRate; T = rocObj.Metrics(idx_b,:).Threshold; idx_model = find(T>=0,1,"last"); modelptb = [T(idx_model) X(idx_model) Y(idx_model)]
modelptb = 1×3
1.2654 0.0179 0.5806
For binary classification, an optimal operating point that minimizes the average misclassification cost is a point at which the ROC curve intersects a straight line with slope , where is defined as
.
is the total number of observations in the positive class, and is the total number of observations in the negative class. The cost values are the components of the cost matrix :
cost(N|P) is the cost of misclassifying a positive class as a negative class, and cost(P|N) is the cost of misclassifying a negative class as a positive class. According to the class order in Mdl.ClassNames, the positive class P corresponds to class b.
Among the points on the ROC curve that intersect a line with slope , choose one that is closest to the perfect classifier point (FPR = 0, TPR = 1), which the perfect ROC curve passes.
Find the optimal operating point for the positive class b.
p = sum(strcmp(YTest,"b")); n = sum(~strcmp(YTest,"b")); cost = Mdl.Cost; m = (cost(2,1)-cost(2,2))/(cost(1,2)-cost(1,1))*n/p; [~,idx_opt] = min(X - Y/m); optpt = [T(idx_opt) X(idx_opt) Y(idx_opt)]
optpt = 1×3
-1.1978 0.1071 0.7742
Plot the ROC curve for class b by using the plot function, which by default also shows the model operating point.
figure
r = plot(rocObj,ClassNames="b");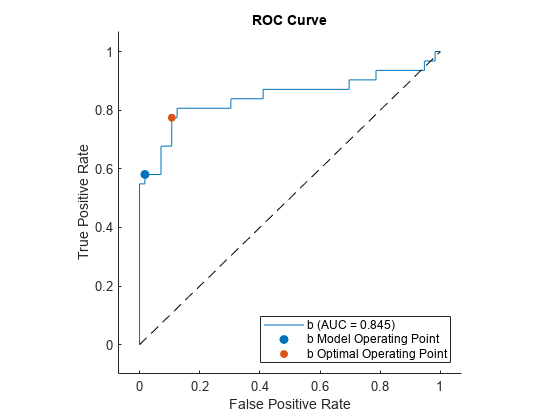
Display the model operating point and the optimal operating point.
modelpt(3,:) = table({"b optimal"},optpt(1),optpt(2),optpt(3))modelpt=3×4 table
ClassName Threshold FalsePositiveRate TruePositiveRate
_______________ _________ _________________ ________________
{'b' } 1.2654 0.017857 0.58065
{'g' } 0.21911 0.41935 0.98214
{["b optimal"]} -1.1978 0.10714 0.77419
Classify XTest using the optimal operating point. Assign an observation whose adjusted score is greater than or equal to the optimal threshold to the positive class b.
s = Scores(:,1) - Scores(:,2);
idx_b_opt = (s >= optpt(1));
Y2 = cell(size(YTest));
Y2(idx_b_opt) = {'b'};
Y2(~idx_b_opt) = {'g'};Display the adjusted scores for the observations that have different labels in Y1 (labels from the predict function) and Y2 (labels from the optimal threshold optpt(1)).
s(~strcmp(Y1,Y2))
ans = 11×1
-1.1703
-0.8445
-0.8235
-0.4546
-1.0719
-0.4612
-0.2191
-1.1978
-1.0114
-1.1552
-0.4525
⋮
Eleven observations have adjusted scores less than 0 but greater than or equal to the optimal threshold.
After training a model for a multiclass classification problem, create a rocmetrics object for classes of interest only. Specify FixedMetricValues so that rocmetrics computes the performance metrics for the specified threshold values.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Partition the data using cvpartition.
rng("default") % For reproducibility of the partition c = cvpartition(creditrating.Rating,"Holdout",0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set creditTrain = creditrating(trainingIndices,:); creditTest = creditrating(testIndices,:);
Train a neural network classifier by passing the training data creditTrain to the fitcnet function.
Mdl = fitcnet(creditTrain,"Rating");Compute classification scores and predict credit ratings for the test set observations.
[labels,Scores] = predict(Mdl,creditTest);
The classification scores for a neural network classifier correspond to posterior probabilities.
Assume that you want to evaluate the model only for the ratings B, BB, and BBB, and ignore the rest of the ratings.
Display the order of the ratings in the model stored in the ClassNames property, and identify the classes to evaluate.
Mdl.ClassNames
ans = 7×1 cell
{'A' }
{'AA' }
{'AAA'}
{'B' }
{'BB' }
{'BBB'}
{'CCC'}
idx_Class = [4 5 6]; classesToEvaluate = Mdl.ClassNames(idx_Class);
Find the indices of the observations for the three classes (B, BB, BBB).
idx = ismember(creditTest.Rating,classesToEvaluate);
Create a rocmetrics object using the true labels and scores for the three classes. Specify FixedMetricValues=1:-0.25:-1 so that rocmetrics computes the performance metrics for the specified threshold values.
thresholds = 1:-0.25:-1;
rocObj = rocmetrics(creditTest.Rating(idx),Scores(idx,idx_Class), ...
classesToEvaluate,FixedMetricValues=thresholds);Display the computed metrics stored in the Metrics property.
rocObj.Metrics
ans=27×4 table
ClassName Threshold FalsePositiveRate TruePositiveRate
_________ _________ _________________ ________________
{'B' } 0.88486 0 0
{'B' } 0.75539 0 0.125
{'B' } 0.53799 0.007732 0.29688
{'B' } 0.28624 0.025773 0.40625
{'B' } 0.018163 0.048969 0.60938
{'B' } -0.24604 0.10825 0.70312
{'B' } -0.49291 0.16753 0.76562
{'B' } -0.74996 0.49485 0.85938
{'B' } -0.98175 1 1
{'BB'} 0.97686 0 0
{'BB'} 0.75173 0.048689 0.19459
{'BB'} 0.51473 0.10112 0.46486
{'BB'} 0.2525 0.14607 0.61081
{'BB'} 0.010893 0.22472 0.74595
{'BB'} -0.24496 0.33708 0.84324
{'BB'} -0.49501 0.45693 0.94054
⋮
The Metrics property contains the performance metrics for the three ratings B, BB, and BBB and the specified threshold values only. The default UseNearestNeighbor value is true if rocmetrics does not compute confidence intervals. Therefore, for each specified threshold value, rocmetrics selects an adjusted score value nearest to the specified value and uses the nearest value as a threshold. Display the specified threshold values and the actual threshold values used for each class.
idx_B = strcmp(rocObj.Metrics.ClassName,"B"); idx_BB = strcmp(rocObj.Metrics.ClassName,"BB"); idx_BBB = strcmp(rocObj.Metrics.ClassName,"BBB"); table(thresholds',rocObj.Metrics.Threshold(idx_B), ... rocObj.Metrics.Threshold(idx_BB), ... rocObj.Metrics.Threshold(idx_BBB), ... VariableNames=["Fixed Threshold";string(classesToEvaluate)])
ans=9×4 table
Fixed Threshold B BB BBB
_______________ ________ ________ ________
1 0.88486 0.97686 0.93468
0.75 0.75539 0.75173 0.75023
0.5 0.53799 0.51473 0.50019
0.25 0.28624 0.2525 0.25729
0 0.018163 0.010893 0.014322
-0.25 -0.24604 -0.24496 -0.23974
-0.5 -0.49291 -0.49501 -0.49572
-0.75 -0.74996 -0.74376 -0.74861
-1 -0.98175 -0.93468 -0.97686
More About
A ROC curve shows the true positive rate versus the false positive rate for different thresholds of classification scores.
The true positive rate and the false positive rate are defined as follows:
True positive rate (TPR), also known as recall or sensitivity —
TP/(TP+FN), where TP is the number of true positives and FN is the number of false negativesFalse positive rate (FPR), also known as fallout or 1-specificity —
FP/(TN+FP), where FP is the number of false positives and TN is the number of true negatives
Each point on a ROC curve corresponds to a pair of TPR and FPR values for a specific
threshold value. You can find different pairs of TPR and FPR values by varying the
threshold value, and then create a ROC curve using the pairs. For each class,
rocmetrics uses all distinct adjusted score values
as threshold values to create a ROC curve.
For a multiclass classification problem, rocmetrics formulates a set
of one-versus-all binary
classification problems to have one binary problem for each class, and finds a ROC
curve for each class using the corresponding binary problem. Each binary problem
assumes one class as positive and the rest as negative.
For a binary classification problem, if you specify the classification scores as a
matrix, rocmetrics formulates two one-versus-all binary
classification problems. Each of these problems treats one class as a positive class
and the other class as a negative class, and rocmetrics finds two
ROC curves. Use one of the curves to evaluate the binary classification
problem.
For more details, see ROC Curve and Performance Metrics.
The area under a ROC curve (AUC) corresponds to the integral of a ROC curve
(TPR values) with respect to FPR from FPR = 0 to FPR = 1.
The AUC provides an aggregate performance measure across all possible thresholds. The AUC
values are in the range 0 to 1, and larger AUC values
indicate better classifier performance.
The one-versus-all (OVA) coding design reduces a multiclass classification
problem to a set of binary classification problems. In this coding design, each binary
classification treats one class as positive and the rest of the classes as negative.
rocmetrics uses the OVA coding design for multiclass classification and
evaluates the performance on each class by using the binary classification that the class is
positive.
For example, the OVA coding design for three classes formulates three binary classifications:
Each row corresponds to a class, and each column corresponds to a binary
classification problem. The first binary classification assumes that class 1 is a positive
class and the rest of the classes are negative. rocmetrics evaluates the
performance on the first class by using the first binary classification problem.
The model operating point represents the FPR and TPR corresponding to the typical threshold value.
The typical threshold value depends on the input format of the Scores argument (classification scores) specified when you create a
rocmetrics object:
If you specify
Scoresas a matrix,rocmetricsassumes that the values inScoresare the scores for a multiclass classification problem and uses adjusted score values. A multiclass classification model classifies an observation into a class that yields the largest score, which corresponds to a nonnegative score in the adjusted scores. Therefore, the threshold value is0.If you specify
Scoresas a column vector,rocmetricsassumes that the values inScoresare posterior probabilities of the class specified inClassNames. A binary classification model classifies an observation into a class that yields a higher posterior probability, that is, a posterior probability greater than0.5. Therefore, the threshold value is0.5.
For a binary classification problem, you can specify Scores as a
two-column matrix or a column vector. However, if the classification scores are not
posterior probabilities, you must specify Scores as a matrix. A binary
classifier classifies an observation into a class that yields a larger score, which is
equivalent to a class that yields a nonnegative adjusted score. Therefore, if you specify
Scores as a matrix for a binary classifier,
rocmetrics can find a correct model operating point using the same
scheme that it applies to a multiclass classifier. If you specify classification scores that
are not posterior probabilities as a vector, rocmetrics cannot identify a
correct model operating point because it always uses 0.5 as a threshold
for the model operating point.
The plot function displays a filled circle marker at the model
operating point for each ROC curve (see ShowModelOperatingPoint). The function chooses a point corresponding to the
typical threshold value. If the curve does not have a data point for the typical threshold
value, the function finds a point that has the smallest threshold value greater than the
typical threshold. The point on the curve indicates identical performance to the performance
of the typical threshold value.
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [2] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [3] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the loss and
predict object functions), which measures how well an ECOC classifier
performs as a whole.
Algorithms
For each class, rocmetrics adjusts the classification scores (input argument
Scores of rocmetrics) relative to the scores for the rest
of the classes if you specify Scores as a matrix. Specifically, the
adjusted score for a class given an observation is the difference between the score for the
class and the maximum value of the scores for the rest of the classes.
For example, if you have [s1,s2,s3] in a row of Scores for a classification problem with
three classes, the adjusted score values are [s1-max(s2,s3),s2-max(s1,s3),s3-max(s1,s2)].
rocmetrics computes the performance metrics using the adjusted score values
for each class.
For a binary classification problem, you can specify Scores as a
two-column matrix or a column vector. Using a two-column matrix is a simpler option because
the predict function of a classification object returns classification
scores as a matrix, which you can pass to rocmetrics. If you pass scores in
a two-column matrix, rocmetrics adjusts scores in the same way that it
adjusts scores for multiclass classification, and it computes performance metrics for both
classes. You can use the metric values for one of the two classes to evaluate the binary
classification problem. The metric values for a class returned by
rocmetrics when you pass a two-column matrix are equivalent to the
metric values returned by rocmetrics when you specify classification scores
for the class as a column vector.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[3] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
[4] Fawcett, T. “ROC Graphs: Notes and Practical Considerations for Researchers”, Machine Learning 31, no. 1 (2004): 1–38.
[5] Zweig, M., and G. Campbell. “Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical Medicine.” Clinical Chemistry 39, no. 4 (1993): 561–577.
[6] Davis, J., and M. Goadrich. “The Relationship Between Precision-Recall and ROC Curves.” Proceedings of ICML ’06, 2006, pp. 233–240.
[7] Moskowitz, C. S., and M. S. Pepe. “Quantifying and Comparing the Predictive Accuracy of Continuous Prognostic Factors for Binary Outcomes.” Biostatistics 5, no. 1 (2004): 113–27.
[8] Huang, Y., M. S. Pepe, and Z. Feng. “Evaluating the Predictiveness of a Continuous Marker.” U. Washington Biostatistics Paper Series, 2006, 250–61.
[9] Briggs, W. M., and R. Zaretzki. “The Skill Plot: A Graphical Technique for Evaluating Continuous Diagnostic Tests.” Biometrics 64, no. 1 (2008): 250–256.
[10] Bettinger, R. “Cost-Sensitive Classifier Selection Using the ROC Convex Hull Method.” SAS Institute, 2003.
[11] DiCiccio, Thomas J., and Bradley Efron. “Bootstrap Confidence Intervals.” Statistical Science 11, no. 3 (1996): 189–228.
[12] Efron, Bradley, and Robert J. Tibshirani. An Introduction to the Bootstrap. New York: Chapman & Hall, 1993.
[13] Efron, Bradley. The Jackknife, the Bootstrap and Other Resampling Plans. Philadelphia: The Society for Industrial and Applied Mathematics, 1982.
[14] Davison, A. C., and D. V. Hinkley. Bootstrap Methods and Their Applications. Cambridge University Press, 1997.
Extended Capabilities
To run bootstrap iterations in parallel, specify the BootstrapOptions
name-value argument when you create a rocmetrics object and set the
UseParallel field of the options structure to true
using statset.
For example:
NumBootstraps=1000,BootstrapOptions=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2022arocmetrics accepts a trained classification model with predictor data
and class labels as inputs instead of Labels,
Scores, and ClassNames. The model can also be
a trained cross-validated classification model, in which case the predictor data and labels
are not required.
rocmetrics has several changes and extensions:
The new
aucfunction computes the AUC of some named curves. Arocmetricsobject no longer has anAUCproperty.The new
modelOperatingPointfunction returns the model performance for each class.The
AverageROCTypename-value argument of theplotfunction is renamedAverageCurveType, and applies to non-ROC curves as well as ROC curves.The model operating point can be plotted using the
ShowModelOperatingPointname-value argument of theplotfunction. The operating point is displayed for averaged curves as well as nonaveraged curves.The
averagefunction is extended to compute the average of any two metrics.The
AdditionalMetricsname-value argument ofrocmetricshas new values:'f1score', which computes the F1 score;'precision', which is the same as'ppv'and'prec'; and'all', which computes all supported metrics.The
metricsinput argument of theaddMetricsfunction takes the same new values as theAdditionalMetricsname-value argument ofrocmetrics.
If you use nondefault misclassification costs by specifying the Cost name-value argument,
and you use scores for a KNN, discriminant analysis, or naive Bayes model, set the ApplyCostToScores name-value
argument to true. Because these models use expected classification costs
rather than scores to predict labels, this setting enables the function to transform the
scores appropriately.
For an example, see Plot ROC Curves for Discriminant Analysis Classifier with Misclassification Costs.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)