probplot
Probability plots
Syntax
Description
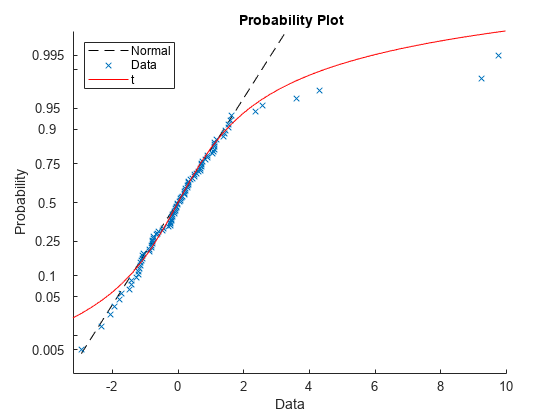
probplot( creates a normal
probability plot comparing the distribution of the data in
y)y to the normal distribution.
probplot plots each data point in
y using marker symbols and draws a reference line that
represents the theoretical distribution. If the sample data has a normal
distribution, then the data points appear along the reference line. The
reference line connects the first and third quartiles of the data and extends to
the ends of the data. A distribution other than normal introduces curvature in
the data plot.
probplot( adds a
probability plot into the existing probability plot axes specified by
ax,___)ax, using any of the input arguments in the previous
syntaxes.
probplot(___,'noref') omits the reference
line from the plot.
Examples
Input Arguments
Output Arguments
Algorithms
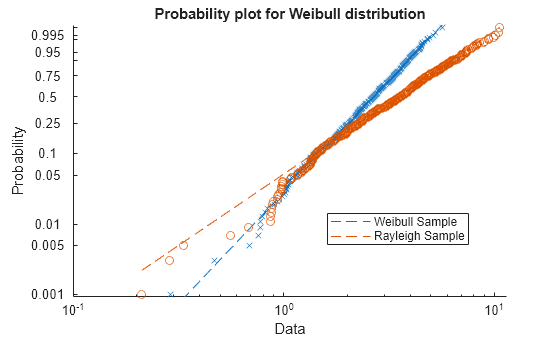
probplot matches the quantiles of sample data to the quantiles of
a given probability distribution. The sample data is sorted, scaled according to the
choice of dist, and plotted on the x-axis. When
dist is 'lognormal',
'loglogistic', or 'weibull', the scaling is
logarithmic. Otherwise, the scaling is linear. The y-axis represents the quantiles of
the distribution specified in dist, converted into probability
values. The scaling depends on the given distribution and is not linear.
Where the x-axis value is the ith sorted value from a sample of size N, the y-axis value is the midpoint between evaluation points of the empirical cumulative distribution function of the data. In the case of uncensored data, the midpoint is equal to .
probplot superimposes a reference line to assess the linearity of
the plot. If the data is uncensored, then the line goes through the first and third
quartiles of the data. If the data is censored, then the line shifts accordingly. If the
data is uncensored and dist is 'half normal', then
probplot uses the zeroth and second quartiles instead.
Version History
Introduced before R2006a