Nonlinear Reluctance
Linear or nonlinear reluctance with optional hysteresis
Libraries:
Simscape /
Electrical /
Passive
Description
The Nonlinear Reluctance block models linear or nonlinear reluctance with optional magnetic hysteresis. Use this block to model custom inductances and build transformer models. To connect this block to your electrical network, use an Electromagnetic Converter block or a Winding block to represent the interface between the electrical and magnetic domains.
To define the geometry for the part of the magnetic network that you are modeling, use the Effective length and Effective cross-sectional area parameters. The block uses this geometry information to map B and H to the magnetomotive force and magnetic flux, which are the Through and Across variables in the magnetic domain. Choose how to parameterize the B-H curve using the Parameterized by parameter.
Equations for Linear Reluctance Parameterization
The equations for the linear reluctance parameterization are
where:
B is the flux density.
μ0 is the permeability in a vacuum.
μr is the relative magnetic permeability.
H is the field strength.
mmf is the magnetomotive force (mmf) across the component.
leff is the effective length of the section being modeled.
φ is the magnetic flux.
seff is the effective cross-sectional area of the section being modeled.
Equations for Reluctance with Single Saturation Point Parameterization
This parameterization models a switch-linear reluctance. In the unsaturated state, the material has a specified relative magnetic permeability. In the saturated state, the relative permeability is 𝜇0.
The equations for reluctance with single saturation point are
If ,
Otherwise,
where:
mmf is the magnetomotive force (mmf) across the component.
leff is the effective length of the section being modeled.
H is the field strength.
φ is magnetic flux.
seff is the effective cross-sectional area of the section being modeled.
B is the flux density.
Bsat is the flux density at saturation.
Rsat is the magnetic reluctance at saturation.
μ0 is the permeability in a vacuum.
μr is the relative magnetic permeability.
μr_unsat is the unsaturated relative magnetic permeability.
Reluctance (B-H Curve)
To model reluctance without hysteresis by tabulating the
B-H curve, set the Parameterized
by parameter to Reluctance (B-H
curve).
Equations for Reluctance with Hysteresis Parameterization
These equations define the flux density and magnetomotive force,
where:
B is the magnetic flux density induced in the core.
φ is the magnetic flux.
seff is the value of the Effective cross-sectional area parameter.
mmf is the magnetomotive force (mmf) across the component.
leff is the value of the Effective length parameter.
H is the total field strength.
This equation relates B and H to the total magnetization of the core M,
where μ0 is the magnetic permeability of a vacuum.
The magnetization acts to increase the magnetic flux density, and its value depends on both the current value and the history of the field strength. The block uses the Jiles-Atherton [1, 2] equations to determine M at any given time. This figure shows a typical plot of the resulting relationship between B and H.
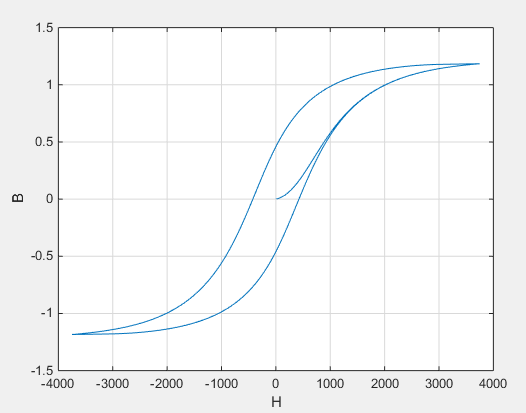
As the field strength increases from H = 0, the plot initially follows an ascending hysteresis curve. At the saturation point, further increases in field intensity no longer cause significant increases in magnetic flux.
As you reduce the magnetic field strength from the saturation point, the plot follows a descending hysteresis curve. The difference between ascending and descending curves is due to the dependence of M on the trajectory history. Physically, the behavior corresponds to magnetic dipoles in the core aligning as the field strength increases, but not then fully recovering to their original position as field strength decreases.
The starting point for the Jiles-Atherton equation is the split of the magnetization effect into two parts, one part that is purely a function of effective field strength Heff and another, irreversible part that depends on history. This equation defines the relative contributions of the anhysteretic magnetisation Man and the irreversible magnetization Mirr to the total magnetization M,
where c is the coefficient for reversible magnetization.
This equation relates Man to the equivalent magnetization Heff:
The function defines a saturation curve with limiting values ±Ms, where:
Ms is the saturation magnetization.
a is the anhysteretic magnetization coefficient, which determines the point of saturation. It approximately describes the average of the two hysteretic curves.
In the Nonlinear Reluctance block mask, you provide values for when Heff = 0 and a point [H1, B1] on the anhysteretic B-H curve. The block uses these values to determine values for α and Ms.
The Jiles-Atherton model defines the irreversible term by a partial derivative with respect to field strength,
where:
K is the bulk coupling coefficient, which shapes the irreversible characteristic.
α is the inter-domain coupling factor.
Comparison of the equation with a standard first-order differential equation reveals that as you change the total field strength H, the irreversible term Mirr attempts to track the reversible term Man, but with a variable tracking gain of . The tracking error acts to create the hysteresis at the points where δ changes sign.
This equation defines the effective field strength of an anhysteretic curve,
The value of α affects the shape of the hysteresis curve. Larger values act to increase the B-axis intercepts. However, the stability term must be positive for δ > 0 and negative for δ < 0. There are therefore limits on the values of α that you can provide. A typical maximum value is of the order 1e-3.
Note
You can also use the Magnetic Core block to model a magnetic core that exhibits nonlinear reluctance and hysteresis. Both blocks use the Jiles-Atherton model to determine the relationship between B, H, and M. However, the Magnetic Core block gives you additional options:
In addition to specifying the Jiles-Atherton parameters directly, you can parameterize the B-H curve using these options:
Specify the magnitude of the B and H intercepts and the magnitude of B and H at the saturation point.
Tabulate the ascending or descending B-H curves.
You can model eddy losses and thermal effects.
You can determine representative values for the equation coefficients using this procedure:
Provide a value for the Anhysteretic B-H gradient when H is zero parameter ( when Heff = 0) and a data point [H1, B1] on the anhysteretic B-H curve. From these values, the block initialization determines values for α and Ms.
Set the Coefficient for reversible magnetization, c parameter to achieve correct initial B-H gradient when starting a simulation from [H B] = [0 0]. The value of c is approximately the ratio of this initial gradient to the Anhysteretic B-H gradient when H is zero. The value of c must be greater than 0 and less than 1.
Set the Bulk coupling coefficient, K parameter to the approximate magnitude of H when B = 0 on the ascending hysteresis curve.
Start with a very small value for the Inter-domain coupling factor, alpha parameter, and gradually increase it to tune the value of B when crossing the H = 0 line. A typical value is in the range of 1e-4 to 1e-3. Values that are too large cause the gradient of the B-H curve to tend to infinity, which is nonphysical and generates a run-time assertion error.
To get a good match against a predefined B-H curve, iterate on these four steps.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
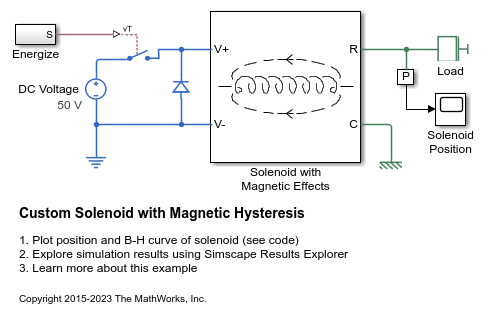
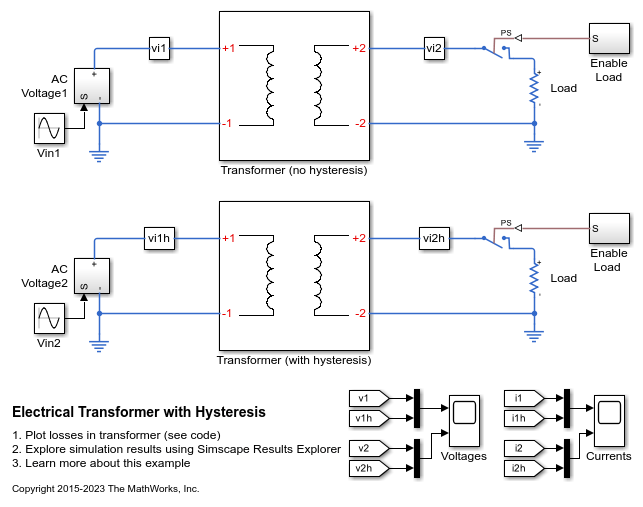
Examples
Ports
Conserving
Parameters
References
[1] Jiles, D. C. and D. L. Atherton. "Theory of ferromagnetic hysteresis." Journal of Magnetism and Magnetic Materials 61, no. 1–2 (September 1986): 48–60. https://doi.org/10.1016/0304-8853(86)90066-1.
[2] Jiles, D. C. and D. L. Atherton. “Ferromagnetic hysteresis.” IEEE® Transactions on Magnetics 19, no. 5 (September 1983): 2183–2185. https://doi.org/10.1109/TMAG.1983.1062594.
Extended Capabilities
Version History
Introduced in R2017b