Suppress Resonances Using Extremum Seeking Control and Frequency Response Estimator Based Adaptive Notch Filter
This example shows how to suppress resonances using an adaptive notch filter. Resonances are commonly present in dynamic systems. These resonances can have a negative affect on system performance such as producing audible noise, degrading operating life or even causing instability. Because of this, it is desired to avoid exciting system resonances in order to improve system performance. There are numerous methods to compensate for resonances such as using stiffer components, using hardware filters, or using a series of notch filters in software. One other method to reduce the effects of resonances is an Adaptive Notch Filter (ANF). In this example, you develop and implement an ANF to compensate for a resonance in a two inertia coupled system.
Open the model.
scdAdaptiveFilterResonanceInit;
mdl = "scdAdaptiveFilterResonanceStateSpace";
open_system(mdl)Model Overview
The model used in this example is composed of a linear state-space model, notch filter, PID controller, random noise, and a way to set the operating points. The state-space model is derived from a two inertia coupled system with spring and damper. For this example, the load inertia (J2) is changed during simulation to simulate a dispensing process. The PID controller is tuned to balance stability and response time and is set to control the load position of the system. Noise is added to the position output to simulate noise from sensors or other processes.
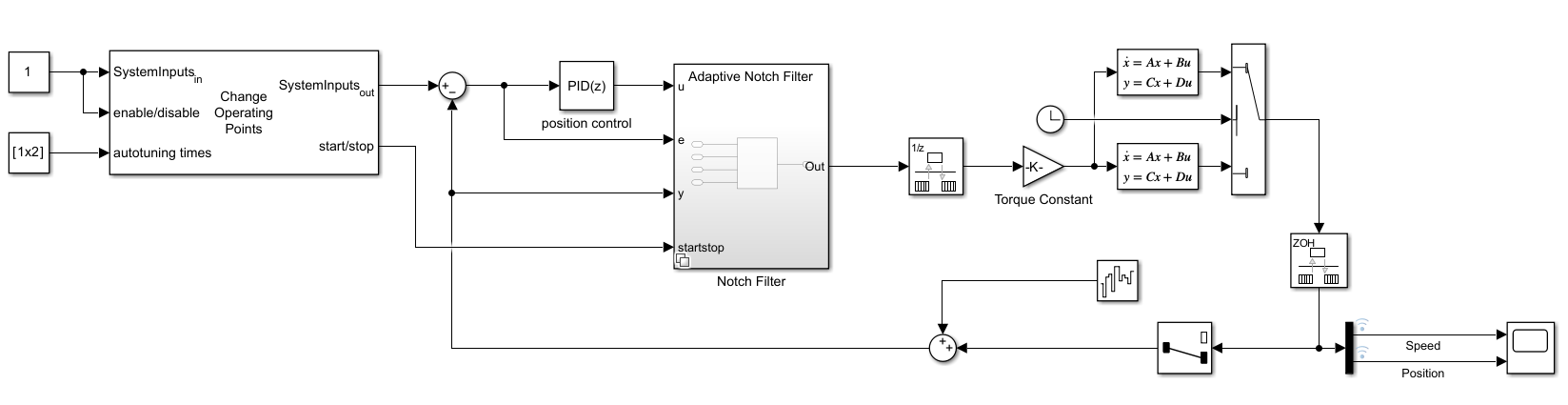
Plant Model
The plant model is based on a two inertia coupled system with a single spring and damper. For this example J1,k, and c remain constant over the course of the simulation but J2 is changed from 60 to 20 to simulate a loss of inertia commonly found in dispensing applications. The load position, , is used in the controller as this is typically measured using a position sensor. In addition, the speed of J1 is used in the results as this speed is also typically measured.
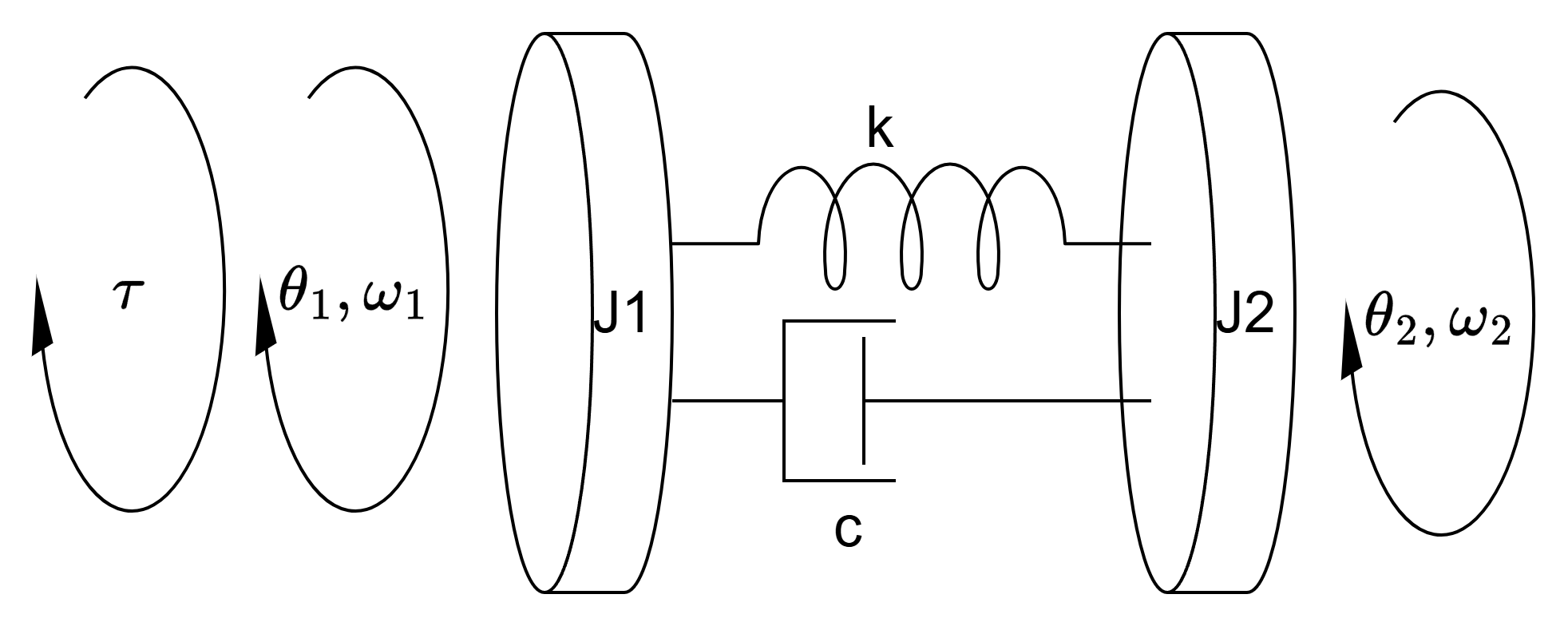
For use in simulation, the model is implemented using the Simulink® State-Space block which is configured to output the states mentioned previously.
Inertia Change
As mentioned in the previous section, the load inertia, J2, is changed during simulation to simulate a dispensing process losing mass. To achieve this two state-space models are used: one for the initial load inertia (J2 = 60) and a second after the load has been dispensed (J2 = 20). Shown below is the bode diagram for the load position, , for these two state-space systems.
% Plot of plant frequency response for position sys1 = ss(A,B,C(2,:),D(2,:)); sys2 = ss(A_2,B_2,C_2(2,:),D_2(2,:)); figure bode(sys1,sys2,{0.1 100}) legend("J2 = 60", "J2 = 20")
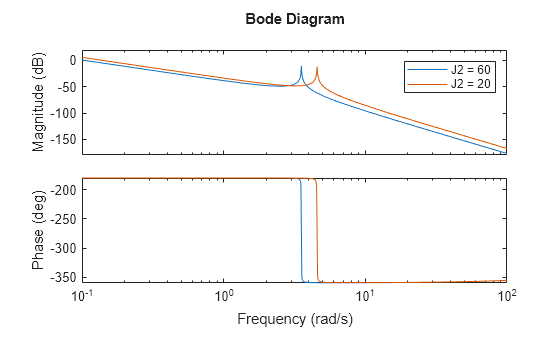
The resonance that is originally present at 3.54 rad/sec but changes to 4.56 rad/sec following the decrease in load inertia.
Compensating for Plant Resonance
The plant resonance that is present initially occurs around 3.54 rad/sec and results in oscillations in both speed and position. Because of this, it is desired to reduce these oscillations which can be done using a notch filter.
Using a notch filter to remove plant resonance
You can use a notch filter to reduce the effect of the resonance seen by the control system. To properly set the parameters for the notch, the resonant frequency must first be determined using the following formula:
One formulation of the notch filter uses explicit settings for the depth of the notch and the width. In this example the values for the width and depth are 0.6 and 0.004, respectively. With all three parameters, you can determine the notch filter transfer function and apply to the state-space system. Plot the bode diagram for the system both with and without the notch filter applied.
% Notch filter gains notchDamp = 0.6; notchGmin = 4e-3; notchSys = tf([1 (2*notchGmin*notchDamp*notchFreq) (notchFreq^2)], [1 (2*notchDamp*notchFreq) (notchFreq^2)]); % Plot Open-Loop Plant with Notch figure bode(sys1,sys1*notchSys,{0.1 100}) legend("Without notch", "With notch")
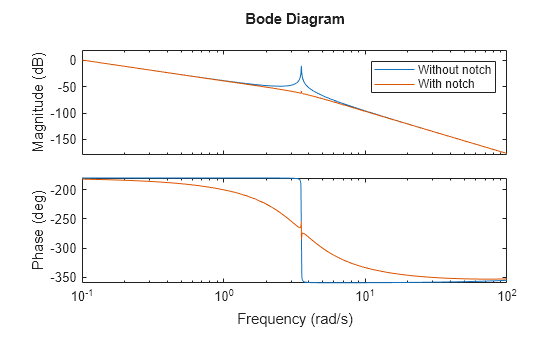
The inclusion of a notch filter placed at the resonant frequency greatly improves the open-loop frequency response of the plant. However, if the notch filter is placed at the wrong frequency then the open-loop plant can be made worse. As shown in the figure below, the notch that is tuned to the frequency of the original plant (J2 = 60) is used on the plant with a lower load inertia (J2 = 20) (shown in red).
% Plot Open-Loop Plant with Notch at J2=60 figure bode(sys2,sys2*notchSys,{0.1 100}) legend("Without notch", "With notch")
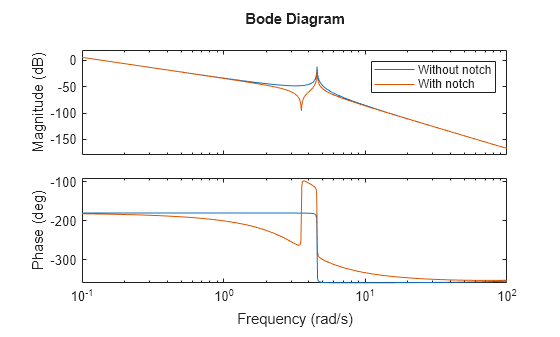
The overall plant response is made worse by using a notch that is set to the wrong frequency. There is now an anti-resonance at the original plants' resonant frequency (3.54 rad/sec) and the phase has been increased as well. From this result, it is clear that a single notch filter at one frequency will not be sufficient for a system whose resonance can change. One solution to this problem is to use a single notch filter that can adapt its frequency placement to handle a changing loading inertia.
Adaptive Notch Filter (ANF) Overview
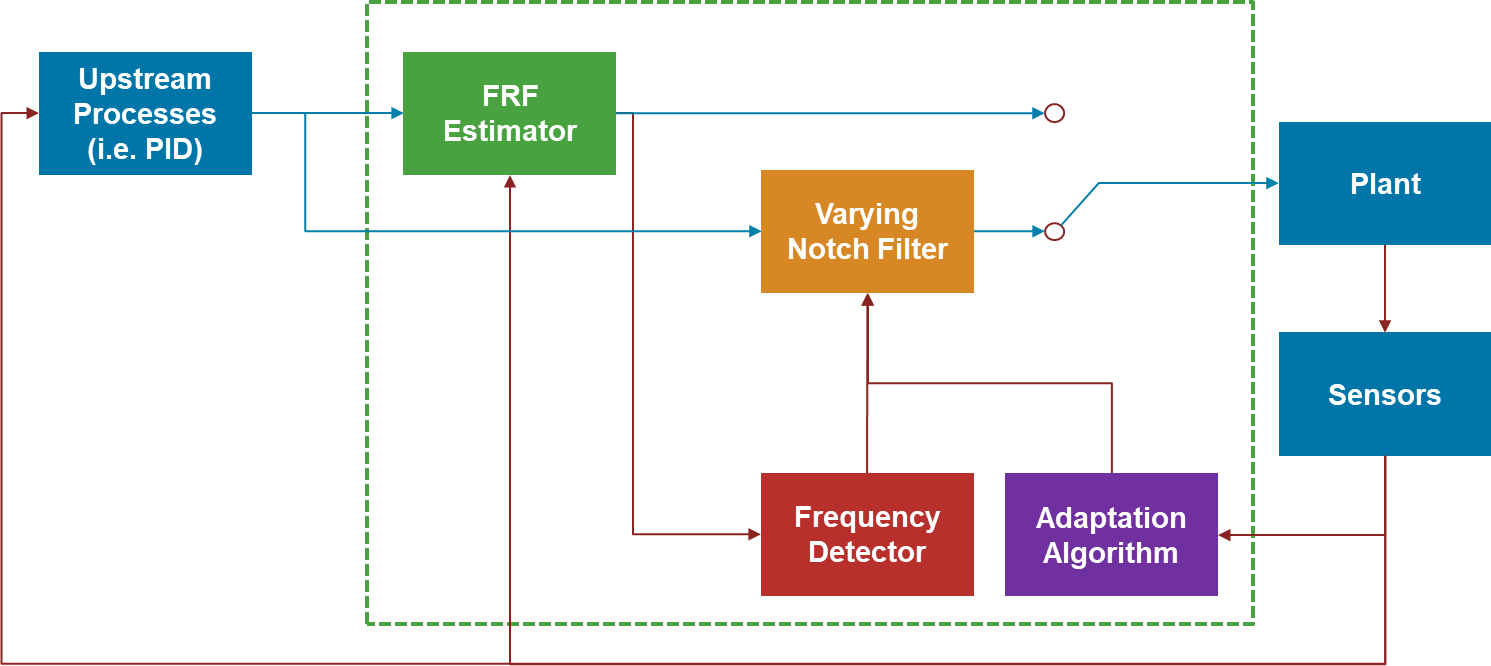
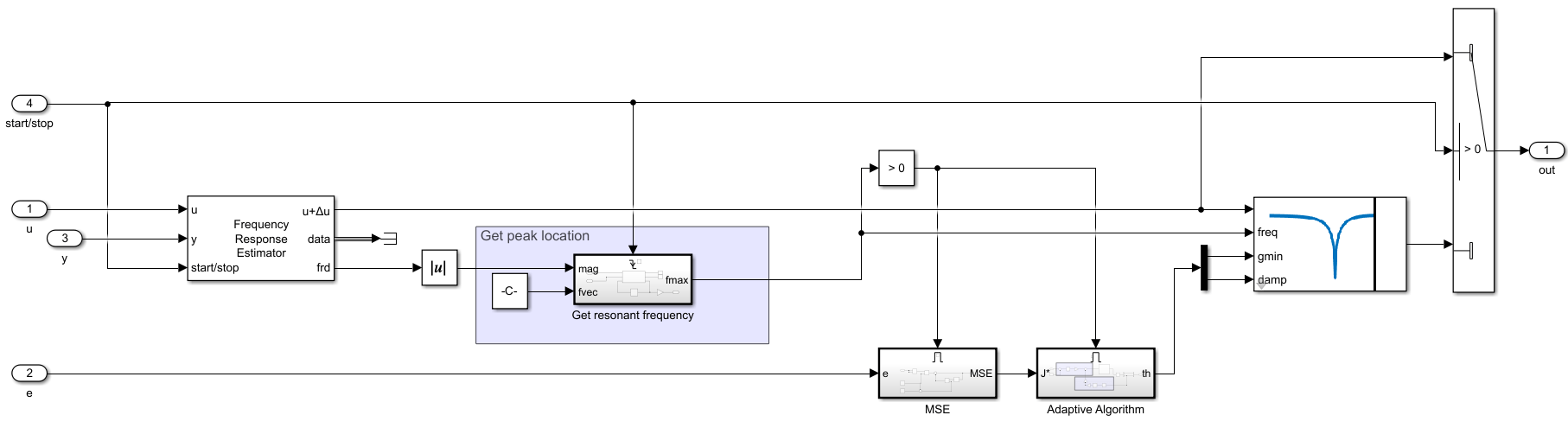
The above image shows a block diagram for the adaptive notch filter (ANF) used in this example. The ANF consists of four main parts:
Adaptation Algorithm
FRF Estimator
Frequency Detector
Notch Filter
For this example the Adaptation Algorithm uses the Extremum Seeking Control block from Simulink® Control Design™ library, the FRF Estimator uses the Frequency Response Estimator (FRE) block, and the Frequency Detector uses the function findpeaks. The FRF estimation and frequency detection portions are enabled when an external start/stop signal is used to trigger the estimation. During this time the notch filter is bypassed and reenabled when a new frequency location for the notch is obtained. The following section discuss the details of these blocks and functions.
Extremum Seeking Control
Extremum seeking control (ESC) is a model-free control algorithm that seeks to maximize an objective function by adjusting parameters through continuous perturbations.
The ESC used in the adaptive notch filter (ANF) uses an objective function based on the mean squared error (MSE) of position and outputs two parameters: notch width and notch depth. The objective function used is shown below where J* is the output of the MSE.
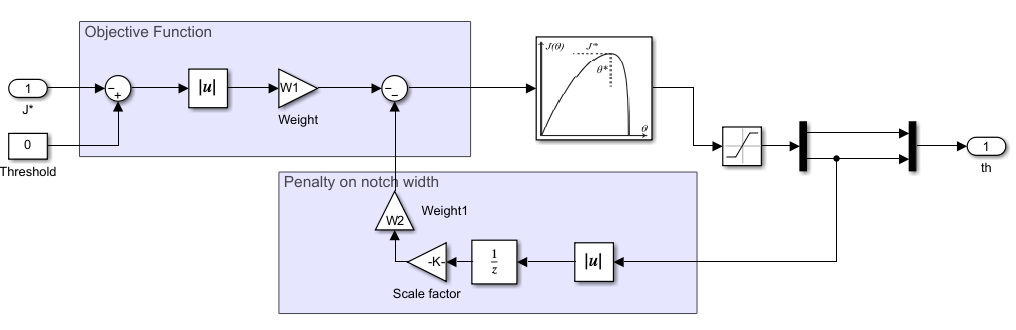
For the MSE calculation, the error used is the same as the input to the PID Controller. The PID Controller can effectively reduce this error to close to zero at all frequencies within its bandwidth but has reduced effectiveness at the resonant frequency. Because of this, during transient operations, the error between the reference and the feedback will be dominated by content at the resonant frequency. In this example, the MSE method used is the traditional exponential moving average:
In the MSE equation, is the smoothing factor () and is the error (input to the PID controller.
As shown in the above image, the objective function uses the MSE and the width of the notch along with their associated weights. In this example, how the parameters for the ESC are set are not detailed but for more information on how the ESC block functions, see Extremum Seeking Control.
Frequency Response Estimation
As mentioned in the previous sections, an estimate of the location of the resonant frequency is required for use in the notch filter. To obtain this estimate, you use the Frequency Response Estimator (FRE) block. This block perturbs the system using either sine waves or pseudorandom binary sequence (PRBS) noise into the system to obtain the frequency response at discrete frequencies. For this example, the PRBS method is used to obtain the frequency response estimate.For more information on the FRE block, see Frequency Response Estimator.
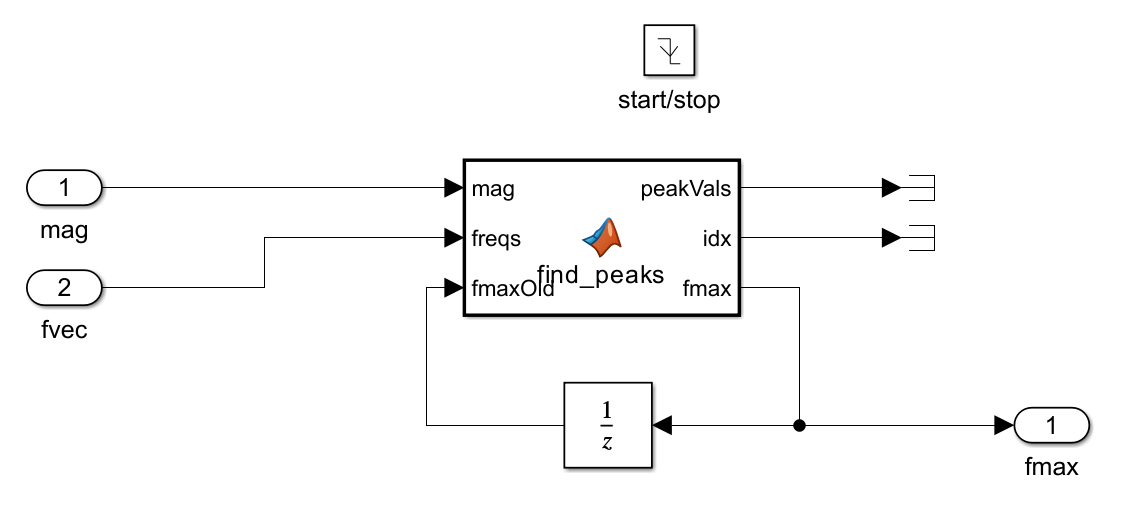
Peak Detection Algorithm
Once the frequency response is determined, the result can be used to determine the location (frequency) of the resonance. To do this a peak detection algorithm can be used. For this example, the MATLAB function findpeaks is used to determine the location of the resonance. This function is used inside of the MATLAB function block. For more information, see findpeaks (Signal Processing Toolbox).
Adaptive Notch Filter
Using the ESC, FRE, and peak detection algorithm together, along with the Discrete Varying Notch Filter block, an adaptive notch filter (ANF) can be created. This ANF will change its depth, width and frequency based on the ESC algorithm and the peak detector.
Using ANF to Reduce Effect of Plant Resonance for Changing Inertia
You can use this adaptive notch filter to handle a plant whose inertia (and thus resonance) changes. For this example, the system is commanded initially to a position of 1 then to position 2 at 1200 seconds. At 1600 seconds, the load inertia (J2) is changed from a value of 60 to 20 simulating a load being dispensed by a servo motor. At 2000 seconds the system is commanded to position 3 then finally to position 4 at 3000 seconds. Between positions 1 and 2 the plant resonance is estimated using the Frequency Response Estimator and then the adaptation algorithm for the adaptive notch filter is enabled. After the load has decreased the plant resonance is reestimated and the location of the notch filter is updated.
This example simulates the model three times and the results of each simulation are compared:
Baseline with no notch filter
Single notch filter set at the
J2=60 resonant frequency (3.54 rad/sec)Adaptive notch filter
% Baseline simulation with no notch filter sim(mdl) baselineResults = logsout; % Simulation with single notch filter tuned at 3.54 rad/sec FilterType = 1; sim(mdl) staticNotchResults = logsout; % Simulation with Adaptive Notch Filter FilterType = 2; sim(mdl) adaptiveNotchResults = logsout;
Compare the results from these three simulations. Plot the speed and position feedback over the entire 3500 second simulation.
figure tiledlayout(2,1); % Position nexttile plot(baselineResults{1}.Values) hold on plot(staticNotchResults{1}.Values) plot(adaptiveNotchResults{1}.Values) hold off legend("No notch","Static notch", "Adaptive notch",Location="southeast") % Speed nexttile plot(baselineResults{2}.Values) hold on plot(staticNotchResults{2}.Values) plot(adaptiveNotchResults{2}.Values) hold off
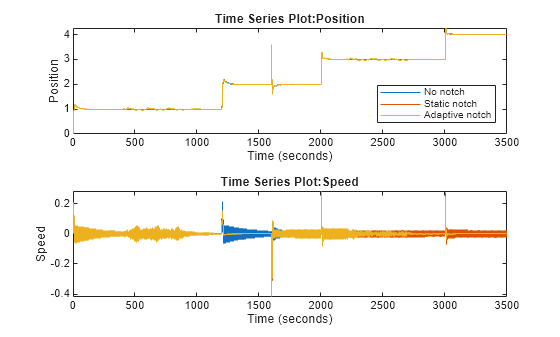
The overall response for the three cases differs significantly over the entire simulation. In order to examine each of the responses more closed, the plot can be zoomed in to each major event. The first plot below shows the initial transient from the initial state to position 1.
figure tiledlayout(2,1); % Position nexttile plot(baselineResults{1}.Values) hold on plot(staticNotchResults{1}.Values) plot(adaptiveNotchResults{1}.Values) hold off xlim([0 50]) legend("No notch","Static notch", "Adaptive notch",Location="southeast") % Speed nexttile plot(baselineResults{2}.Values) hold on plot(staticNotchResults{2}.Values) plot(adaptiveNotchResults{2}.Values) hold off xlim([0 50])
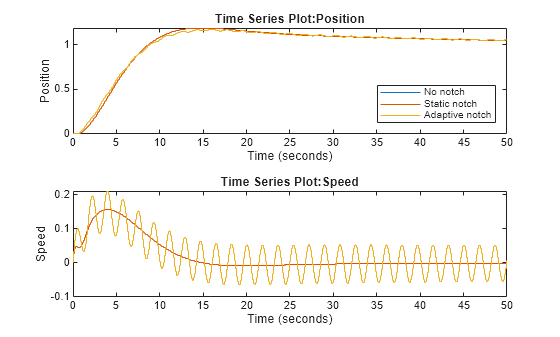
The response for the baseline result and the adaptive notch filter result are the same. This is because the ANF has not yet been tuned. However, the response with the static notch filter shows improved performance due to being tuned and set at the correct resonant frequency. The next plot below shows the transient from position 1 to position 2 after the notch filter has been tuned.
figure tiledlayout(2,1); % Position nexttile plot(baselineResults{1}.Values) hold on plot(staticNotchResults{1}.Values) plot(adaptiveNotchResults{1}.Values) hold off xlim([1200 1250]) legend("No notch","Static notch", "Adaptive notch",Location="southeast") % Speed nexttile plot(baselineResults{2}.Values) hold on plot(staticNotchResults{2}.Values) plot(adaptiveNotchResults{2}.Values) hold off xlim([1200 1250])
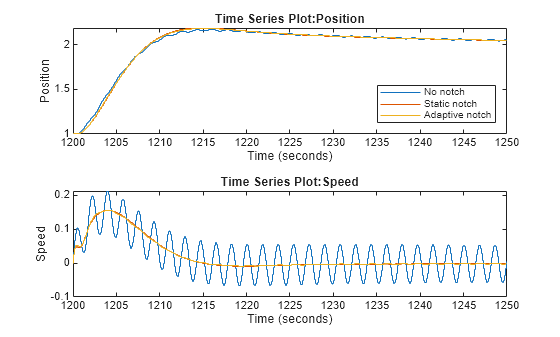
As shown in the above plot the adaptive notch filter response is comparable to the pretuned static notch filter because the ANF is enabled during this transient and its frequency placement was estimated using the frequency response estimator. The next plot below shows the transient from position 2 to position 3 after the load inertia has decreased from 60 to 20.
figure tiledlayout(2,1); % Position nexttile plot(baselineResults{1}.Values) hold on plot(staticNotchResults{1}.Values) plot(adaptiveNotchResults{1}.Values) hold off xlim([2000 2050]) legend("No notch","Static notch", "Adaptive notch",Location="southeast") % Speed nexttile plot(baselineResults{2}.Values) hold on plot(staticNotchResults{2}.Values) plot(adaptiveNotchResults{2}.Values) hold off xlim([2000 2050])
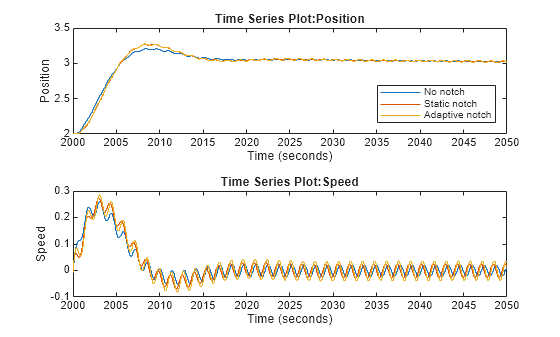
As shown in the above plot all three responses are poor but the simulation with no notch filter has the smallest oscillations. This is consistent with the above discussion showing that an improperly tuned notch filter causes the system performance to degrade compared to having no notch filter. The final plot below shows the final transient from position 3 to position 4 after the adaptive notch filter's frequency has been re-estimated.
figure tiledlayout(2,1); % Position nexttile plot(baselineResults{1}.Values) hold on plot(staticNotchResults{1}.Values) plot(adaptiveNotchResults{1}.Values) hold off xlim([3000 3050]) legend("No notch","Static notch", "Adaptive notch",Location="southeast") % Speed nexttile plot(baselineResults{2}.Values) hold on plot(staticNotchResults{2}.Values) plot(adaptiveNotchResults{2}.Values) hold off xlim([3000 3050])
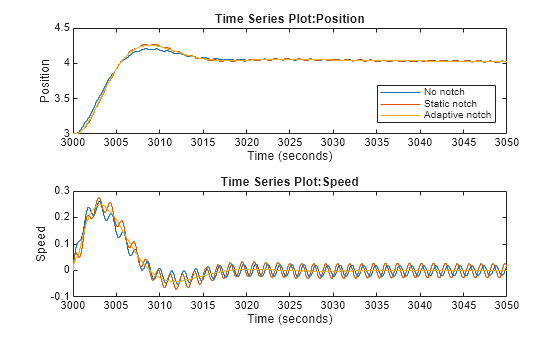
The above plot shows that while the response of the system with no notch filter and a static notch filter have the same performance as before, the response with the adaptive notch filter is greatly improved due to its frequency placement changing to the new resonant frequency of 4.56 rad/sec.
Summary
In this example the resonance of a system is compensated for using a notch filter. The system experiences a change in load inertia causing the resonant frequency to move necessitating the need for either multiple notch filters or a single notch filter that adapts its frequency. The adaptive notch filter in this example successfully changes its frequency placement following the change in load inertia and improves the overall system performance.