pkurtosis
(To be removed) Spectral kurtosis from signal or spectrogram
pkurtosis will be removed in a future release. Use spectralKurtosis instead. For more information, see Version History.
Syntax
Description
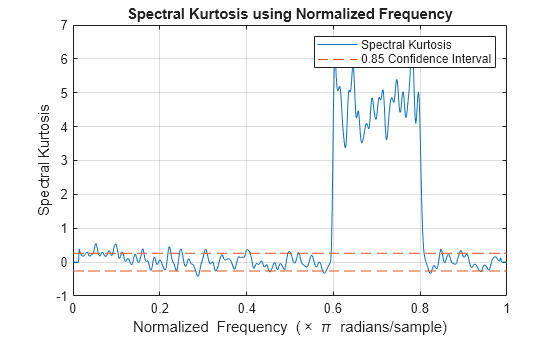
sk = pkurtosis(x)x as the vector
sk. pkurtosis uses normalized
frequency (evenly spaced frequency vector spanning [0 π]) to compute the time
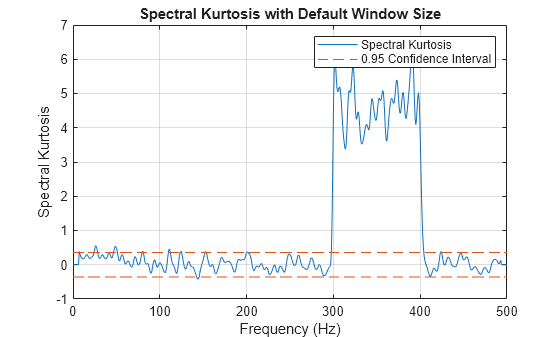
values. pkurtosis computes the spectrogram of
x using pspectrum with default
window size (time resolution in samples), and 80% window overlap.
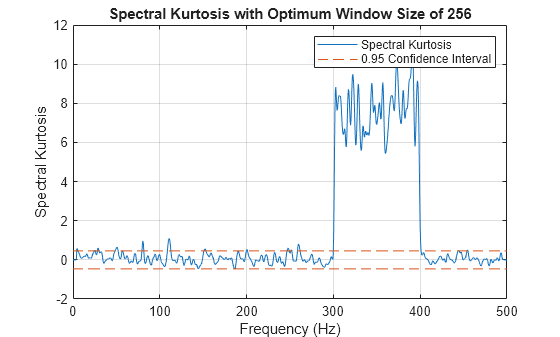
sk = pkurtosis(s,sampx,f,window)s, along with:
Sample rate or time,
sampx, of the original time-series signal that was transformed to producesSpectrogram frequency vector
fSpectrogram time resolution
window
Use this syntax when you want to customize the options for
pspectrum, rather than accept the default
pspectrum options that pkurtosis
applies. You can specify sampx as empty to default to
normalized frequency. Although window is optional for
previous syntaxes, you must supply a value for window when
using this syntax.
[___,returns
the spectral kurtosis threshold thresh] = pkurtosis(___,'ConfidenceLevel',p) thresh using the confidence
level p. thresh represents the range
within which the spectral kurtosis indicates a Gaussian stationary signal, at
the optional confidence level p that you either specify or
accept as default. Specifying p allows you to tune the
sensitivity of the spectral kurtosis thresh results to
behavior that is non-Gaussian or nonstationary. You can use the
thresh output argument with any of the input arguments
in previous syntaxes. You can also set the confidence level in previous
syntaxes, but it has no effect unless you are returning or plotting
thresh.
pkurtosis(___) plots the spectral kurtosis,
along with confidence level and thresholds, without returning any data. You can
use this syntax with any of the input arguments in previous syntaxes.
Examples
Input Arguments
Output Arguments
More About
References
[1] Antoni, J. "The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals." Mechanical Systems and Signal Processing. Vol. 20, Issue 2, 2006, pp. 282–307.
[2] Antoni, J., and R. B. Randall. "The Spectral Kurtosis: Application to the Vibratory Surveillance and Diagnostics of Rotating Machines." Mechanical Systems and Signal Processing. Vol. 20, Issue 2, 2006, pp. 308–331.
Extended Capabilities
Version History
Introduced in R2018aSee Also
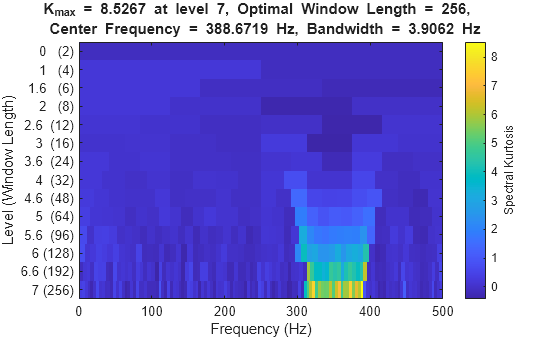
kurtogram | pspectrum | spectralEntropy | spectralKurtosis
Topics
- Rolling Element Bearing Fault Diagnosis (Predictive Maintenance Toolbox)