ifsst
Inverse Fourier synchrosqueezed transform
Syntax
Description
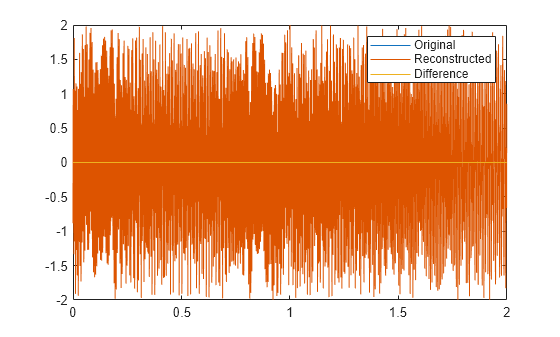
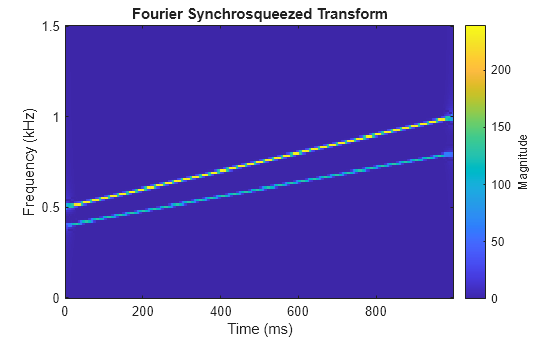
x = ifsst(s,window,iridge)iridge. If iridge is
a matrix, then ifsst initially performs the inversion
along the first column of iridge and then proceeds
iteratively along the subsequent columns. The output is a vector or
matrix with the same size as iridge.