serdes.FFE
Models a feed-forward equalizer
Description
The serdes.FFE
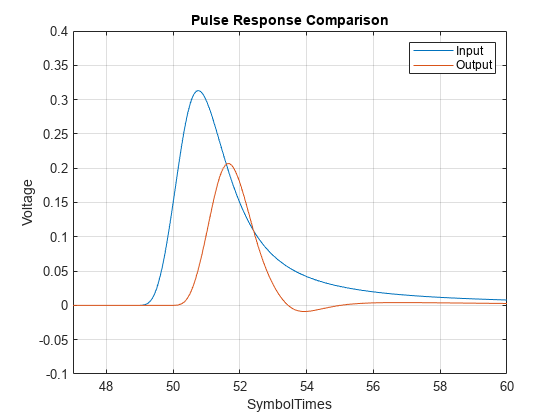
System object™ applies a feed-forward equalizer (FFE) as a symbol-spaced finite-impulse
response (FIR) filter. Apply the equalizer to a sample-by-sample input signal or an impulse
response vector input signal to reduce distortions due to channel loss impairments.
To equalize the baseband signal:
Create the
serdes.FFEobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
ffe = serdes.FFE
ffe = serdes.FFE(Name,Value)
Example: ffe = serdes.FFE('Mode',1) returns an FFE object that
applies specified tap weights to the input waveform.
Properties
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Extended Capabilities
Version History
Introduced in R2019a
See Also
FFE | serdes.CTLE | CTLE