serdes.CTLE

Continuous time linear equalizer (CTLE) or peaking filter

Description

The serdes.CTLE System object™ applies a linear peaking filter to equalize a sample-by-sample input signal or to analytically process an impulse response vector input signal. The equalization process reduces distortions resulting from lossy channels. The filter is a real one-zero two-pole (1z/2p) filter, unless you define the gain-pole-zero (GPZ) matrix.

To equalize the baseband signal using serdes.CTLE:

1. Create the serdes.CTLE object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

ctle = serdes.CTLE

ctle = serdes.CTLE(Name,Value)

Description

ctle = serdes.CTLE returns a CTLE object that modifies an input waveform according to the pole zero transfer function defined in the object.

ctle = serdes.CTLE(Name,Value) sets properties using one or more name-value pairs. Enclose each property name in quotes. Unspecified properties have default values.

Example: ctle = serdes.CTLE('ACGain',5) returns a CTLE object with gain at the peaking frequency set to 5 dB.

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Main

Mode — CTLE operating mode

2 (default) | 0 | 1

CTLE operating mode, specified as 0, 1, or 2. Mode determines whether the CTLE is bypassed or not. If CTLE is not bypassed, then Mode also determines what transfer function is applied to the input waveform.

Mode Value	CTLE Mode	CTLE Operation
0	off	serdes.CTLE is bypassed and the input waveform remains unchanged.
1	fixed	serdes.CTLE applies the CTLE transfer function as specified by ConfigSelect to the input waveform.
2	adapt	If WaveType is set to 'Impulse' or 'Waveform', then the Init subsystem calls to the serdes.CTLE. The serdes.CTLE determines the CTLE transfer function to maximize the performance metric as specified by the PerformanceCriteria property and applies the transfer function to the input waveform for time domain simulation. This optimized transfer function is used by the CTLE for entire time domain simulation. For more information about the Init subsystem, see Statistical Analysis in SerDes Systems
		If WaveType is selected as 'Sample', then serdes.CTLE operates in the fixed mode.

Data Types: double

SliceSelect — Select which corner of 3D GPZ matrix to use

0 (default) | nonegative scalar integer

Select which slice, family, or corner of a 3-D GPZ matrix to use during CTLE configuration.

You must set Specification to GPZ to effectively use SliceSelect. Depending on how many slices are available in your GPZ matrix, you can then select the slice you are interested in from a zero-based index.

You cannot use GPZ for a given slice and the peaking gain, DC gain, or AC gain for another slice.

Data Types: double

ConfigSelect — Select which member of transfer function family to apply in fixed mode

0 (default) | real integer scalar

Select which member of the transfer function family to apply in fixed mode, specified as a real integer scalar.

Example: ctle = serdes.CTLE('ConfigSelect',5,'Specification','DC Gain and Peaking Gain') returns a CTLE object that selects the 6-th element of the DCGain and PeakingGain vector to apply to the filter transfer function.

Data Types: double

Specification — Input specification for CTLE response

'DC Gain and Peaking Gain' (default) | 'DC Gain and AC Gain' | 'AC Gain and Peaking Gain' | 'GPZ Matrix'

Defines which inputs will be used for the CTLE transfer function family. There are five inputs which can be used to define the CTLE transfer function family: DCGain, PeakingGain, ACGain, PeakingFrequency, and GPZ.

You can define the CTLE response from any two of the three gains and peaking frequency or you can define the GPZ matrix for the CTLE.

• Select 'DC Gain and Peaking Gain' to specify CTLE response from DCGain, PeakingGain, and PeakingFrequency.

• 'DC Gain and AC Gain' to specify CTLE response from DCGain, ACGain, and PeakingFrequency.

• 'AC Gain and Peaking Gain' to specify CTLE response from ACGain, PeakingGain, and PeakingFrequency.

• 'GPZ Matrix' to specify CTLE response from GPZ.

Data Types: char

PeakingFrequency — Approximate frequency at which CTLE transfer function peaks

5e9 (default) | scalar | vector

Approximate frequency at which CTLE transfer function peaks in magnitude, specified as a scalar or a vector in Hz. If specified as a scalar, it is converted to match the length of ACGain, DCGain, and PeakingGain by scalar expansion. If specified as a vector, then the vector length must be the same as the vectors in ACGain, DCGain, and PeakingGain.

Data Types: double

DCGain — Gain at zero frequency

[0 -1 -2 -3 -4 -5 -6 -7 -8] (default) | scalar | vector

Gain at zero frequency for the CTLE transfer function, specified as a scalar or a vector in dB. If specified as a scalar, it is converted to match the length of PeakingFrequency, ACGain, and PeakingGain by scalar expansion. If specified as a vector, then the vector length must be the same as the vectors in PeakingFrequency, ACGain, and PeakingGain.

Data Types: double

PeakingGain — Difference between AC and DC gain

[0 1 2 3 4 5 6 7 8] (default) | scalar | vector

Peaking gain, specified as a vector in dB. It is the difference between ACGain and DCGain for the CTLE transfer function. If specified as a scalar, it is converted to match the length of PeakingFrequency, ACGain, and DCGain by scalar expansion. If specified as a vector, then the vector length must be the same as the vectors in PeakingFrequency, ACGain, and DCGain.

Data Types: double

ACGain — Gain at the peaking frequency

0 | scalar | vector

Gain at the peaking frequency for the CTLE transfer function, specified as a scalar or vector in dB. If specified as a scalar, it is converted to match the length of PeakingFrequency, DCGain, and PeakingGain by scalar expansion. If specified as a vector, then the vector length must be the same as the vectors in PeakingFrequency, DCGain, and PeakingGain.

Data Types: double

GPZ — Gain pole zero

matrix

Gain pole zero, specified as a matrix. GPZ explicitly defines the family of CTLE transfer functions by specifying the DCGain (dB) in the first column and then poles and zeros in alternating columns. The poles and zeros are specified in Hz. Use the argument ConfigSelect with zero-based index to select filters defined by rows of the GPZ matrix.

The serdes.CTLE System object only allows repeated poles or zeros when the FilterMethod is set to Cascaded. Complex poles or zeros must have conjugates. The number of poles must be greater than number of zeros for system stability. The System object ignores poles and zeros of 0 Hz and you can use them to zero-pad the matrix.

You can define multiple slices of CTLE responses by using a 3-D GPZ matrix. You can concatenate and zero-pad two GPZ matrices to extend to the third dimension.

Data Types: double
Complex Number Support: Yes

Advanced

SymbolTime — Time of single symbol duration

100e-12 (default) | real scalar

Time of a single symbol duration, specified as a real scalar in s.

Data Types: double

SampleInterval — Uniform time step of waveform

6.25e-12 (default) | real scalar

Uniform time step of the waveform, specified as a real scalar in s.

Data Types: double

WaveType — Input wave type form

'Sample' (default) | 'Impulse' | 'Waveform'

Input wave type form:

• 'Sample' — A sample-by-sample input signal.

• 'Impulse' — An impulse response input signal.

• 'Waveform' — A bit-pattern waveform type of input signal, such as pseudorandom binary sequence (PRBS).

Data Types: char

PerformanceCriteria — Criterion used for CTLE optimization

SNR (default) | maxEyeHeight | maxMeanEyeHeight | maxCOM | eyeAreas | eyeWidth | centerEyeHeight | centerMeanEyeHeight | centerCOM

Criterion used for CTLE optimization when the serdes.CTLE Mode is set to adapt. The performance criteria is calculated using the optPulseMetric function.

Data Types: char

OutputOptMetric — Output optimization metric value

off (default) | on

Output the optimization metric value.

FilterMethod — Method to calculate time domain filter coefficients

PartialFraction (default) | Cascaded

Method to calculate rational transfer function time domain filter coefficients:

• PartialFraction filter method uses a partial fraction expansion of the poles and zeros to directly calculate the filter coefficients. The serdes.CTLE System object does not allow repeated poles or zeros when the FilterMethod is set to PartialFraction.

• Cascaded filter method uses an approach that cascades together numerous shorter filters that collectively represent the specified behavior. This results in a more robust filter. The serdes.CTLE System object only allows repeated poles or zeros when the FilterMethod is set to Cascaded.

Usage

Syntax

y = ctle(x)

Description

y = ctle(x)

Input Arguments

x — Input baseband signal

scalar | vector

Input baseband signal. If the WaveType is set to 'Sample', then the input signal is a sample-by-sample signal specified as scalars. If the WaveType is set to 'Impulse', then the input signal is an impulse response vector signal.

Output Arguments

y — Equalized CTLE output

scalar | vector

Equalized CTLE output waveform. If the input signal is a sample-by-sample signal specified as scalars, then the output is also scalar. If the input signal is an impulse response vector signal, then the output is also a vector.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

Impulse Response Processing Using CTLE

This example shows how to process the impulse response of a channel using serdes.CTLE System object™.

Use a symbol time of 100 ps and 16 samples per symbol. The channel has 16 dB loss. The peaking frequency is 11 GHz.

 SymbolTime = 100e-12;              
 SamplesPerSymbol = 16;
 dbloss = 16;                       
 DCGain = 0:-1:-26;
 PeakingGain = 0:26;
 PeakingFrequency = 11e9;

Calculate the sample interval.

dt = SymbolTime/SamplesPerSymbol;

Create the CTLE object. The object adaptively applies the optimum transfer function for the best eye height opening to the input impulse response.

CTLE1 = serdes.CTLE('SymbolTime',SymbolTime,'SampleInterval',dt,...
      'Mode',2,'WaveType','Impulse',...
      'DCGain',DCGain,'PeakingGain',PeakingGain,...
      'PeakingFrequency',PeakingFrequency);

Create the channel impulse response.

channel = serdes.ChannelLoss('Loss',dbloss,'dt',dt,...
      'TargetFrequency',1/SymbolTime/2);
impulseIn = channel.impulse;

Process the impulse response with CTLE.

[impulseOut, Config] = CTLE1(impulseIn);

Display the adapted configuration.

fprintf('Adapted CTLE Configuration Selection is %g \n',Config)

Adapted CTLE Configuration Selection is 17 

Convert the impulse responses to pulse, waveform, and eye diagram.

ord = 6;
dataPattern = prbs(ord,2^ord-1)-0.5;
 
pulseIn = impulse2pulse(impulseIn,SamplesPerSymbol,dt);
waveIn = pulse2wave(pulseIn,dataPattern,SamplesPerSymbol);
eyeIn = reshape(waveIn,SamplesPerSymbol,[]);
 
pulseOut = impulse2pulse(impulseOut,SamplesPerSymbol,dt);
waveOut = pulse2wave(pulseOut,dataPattern,SamplesPerSymbol);
eyeOut = reshape(waveOut,SamplesPerSymbol,[]);

Create the time vectors.

t = dt*(0:length(pulseOut)-1)/SymbolTime;
teye = t(1:SamplesPerSymbol);
t2 = dt*(0:length(waveOut)-1)/SymbolTime;

Plot pulse response comparison, waveform comparison, input, and output eye diagrams.

figure
plot(t,pulseIn,t,pulseOut)
legend('Input','Output')
title('Pulse Response Comparison')
xlabel('Symbol Times'),ylabel('Voltage')
grid on
axis([47 60 -0.1 0.4]) 

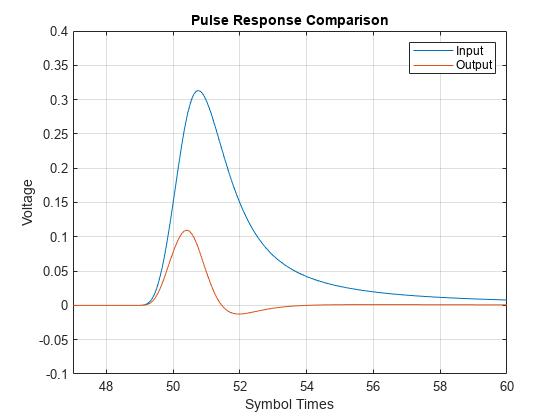
figure
plot(t2,waveIn,t2,waveOut)
legend('Input','Output')
title('Waveform Comparison')
xlabel('Symbol Times'),ylabel('Voltage')
grid on

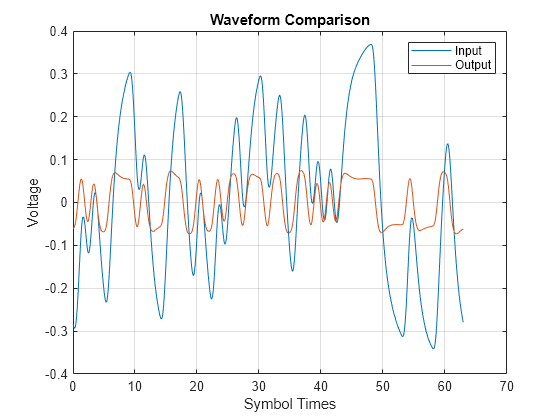
figure
subplot(211),plot(teye,eyeIn,'b')
ax = axis;
xlabel('Symbol Times'),ylabel('Voltage')
grid on
title('Input Eye Diagram')
subplot(212),plot(teye,eyeOut,'b')
axis(ax);
xlabel('Symbol Times'),ylabel('Voltage')
grid on
title('Output Eye Diagram')

Sample-by-Sample Processing Using CTLE

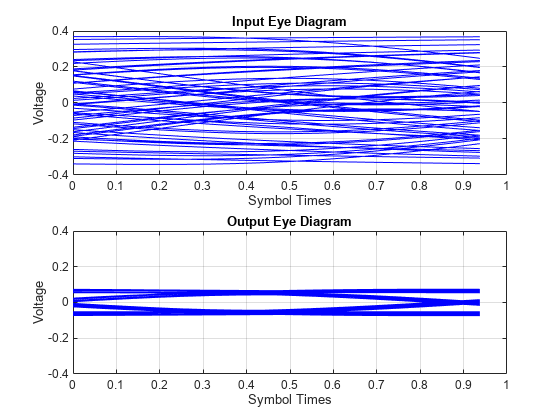
This example shows how to process impulse response of a channel one sample at a time using serdes.CTLE System object™.

Use a symbol time of 100 ps and 16 samples per symbol. The channel has 16 dB loss. The peaking frequency is 11 GHz. Select 12-th order pseudorandom binary sequence (PRBS), and simulate the first 500 symbols.

SymbolTime = 100e-12;           
SamplesPerSymbol = 16;
dbloss = 16;                    
DCGain = 0:-1:-26;
PeakingGain = 0:26;
PeakingFrequency = 11e9;
ConfigSelect = 15;
prbsOrder = 12;                 
M = 500;                     

Calculate the sample interval.

dt = SymbolTime/SamplesPerSymbol;

Create the CTLE object. Since we are processing the channel one sample at a time, the input waveform is 'sample' type. The object adaptively applies the optimum filter transfer function for the best eye height opening.

CTLE = serdes.CTLE('SymbolTime',SymbolTime,'SampleInterval',dt,...
    'Mode',2,'WaveType','Sample',...
    'DCGain',DCGain,'PeakingGain',PeakingGain,...
    'PeakingFrequency',PeakingFrequency,...
    'ConfigSelect',ConfigSelect);

Create the channel impulse response.

channel = serdes.ChannelLoss('Loss',dbloss,'dt',dt,...
    'TargetFrequency',1/SymbolTime/2);

Initialize PRBS generator.

[dataBit,prbsSeed] = prbs(prbsOrder,1);

Loop through one symbol at a time.

inSymbol = zeros(SamplesPerSymbol,1);
  outWave = zeros(SamplesPerSymbol*M,1);
  for ii = 1:M
      % Get new symbol
      [dataBit,prbsSeed] = prbs(prbsOrder,1,prbsSeed);
      inSymbol(1:SamplesPerSymbol) = dataBit-0.5;
 
      % Convolve input waveform with channel
      y = channel(inSymbol);
 
      % Process one sample at a time through the CTLE
      for jj = 1:SamplesPerSymbol
          outWave((ii-1)*SamplesPerSymbol+jj) = CTLE(y(jj));
      end
  end

After truncating the first 75 symbols to allow equalization, use the function reshape on the array of symbols to create the eye diagram.

foldedEye = reshape(outWave(75*SamplesPerSymbol+1:M*SamplesPerSymbol),SamplesPerSymbol,[]);
t = dt*(0:SamplesPerSymbol-1);
figure,plot(t,foldedEye,'b');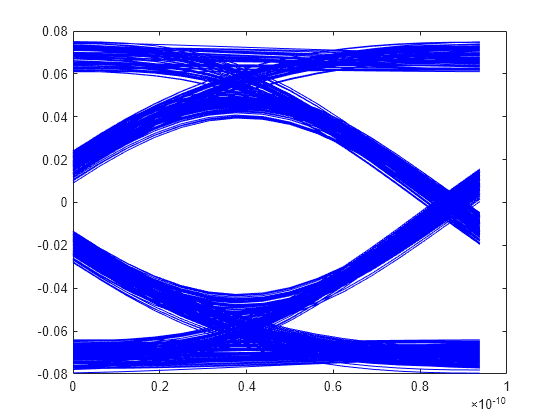

Copyright 2019 The MathWorks, Inc.

Define CTLE from 3D GPZ Matrix

Create a GPZ matrix from a uniform number of poles and zeros.

G = [-3;-4;-5;-6];
P = [-15321428571 -13848214285;...
    -15600000000 -14100000000;...
    -15878571428 -14351785714;...
    -16157142857 -14603571428];
Z = [-5574642857;-4960100000;-4435821428;-3981285714];

gpz1 = serdes.CTLE.GainPoleZeroToGPZ(G,P,Z);

Create a second GPZ matrix from a varying number of poles.

G = [0;-1;-2];
P = {[-23771428571,-13092857142];...
    [-17603571428,-13344642857];...
    [-17935714285,-13596428571,-15321428571]};
Z = {-10492857142;-7914982142;-6845464285};
gpz2 = serdes.CTLE.GainPoleZeroToGPZ(G,P,Z);

Combine the two matrices into a 3D GPZ matrix.

gpz = serdes.CTLE.CombineSlices(gpz1,gpz2)

gpz = 
gpz(:,:,1) =

   1.0e+10 *

   -0.0000   -1.5321   -0.5575   -1.3848         0         0
   -0.0000   -1.5600   -0.4960   -1.4100         0         0
   -0.0000   -1.5879   -0.4436   -1.4352         0         0
   -0.0000   -1.6157   -0.3981   -1.4604         0         0


gpz(:,:,2) =

   1.0e+10 *

         0   -2.3771   -1.0493   -1.3093         0         0
   -0.0000   -1.7604   -0.7915   -1.3345         0         0
   -0.0000   -1.7936   -0.6845   -1.3596         0   -1.5321
         0         0         0         0         0         0

Create a CTLE from the 3D GPZ matrix.

CTLE3D = serdes.CTLE('Specification','GPZ Matrix','GPZ',gpz,'FilterMethod','Cascaded')

CTLE3D = 
  serdes.CTLE with properties:

   Main
             Mode: 2
    Specification: 'GPZ Matrix'
              GPZ: [4x6x2 double]
      SliceSelect: 0
     ConfigSelect: 0

  Use get to show all properties

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

IBIS-AMI codegen is not supported in MAC.

Version History

Introduced in R2019a

R2023b: Slice Select

you can now select which slice, family, or corner of a 3-D GPZ matrix to use during CTLE configuration.