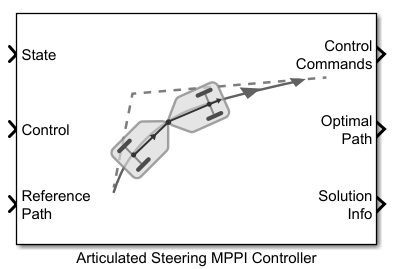
Articulated Steering MPPI Controller

Control motion planning of articulated steering vehicle model using Model Predictive Path Integral (MPPI)

Since R2025b

expand all in page
  • Articulated Steering MPPI Block Icon

Libraries:
Offroad Autonomy Library / Vehicle Controllers

Description

The Articulated Steering MPPI Controller block enables you to plan a local path for a vehicle modeled with articulatedSteeringKinematics object. The block uses the model predictive path integral (MPPI) algorithm and follows a reference path, typically generated by a global planner such as RRT* or Hybrid A*.

The articulated steering vehicle model represents a vehicle with an articulated joint and two axles. The front axle is at an offset specified by the Front Angle Offset (m) parameter from the articulated joint. The rear axle is at an offset specified by the Rear Angle Offset (m) parameter from the articulated joint. The articulated joint is active, which means the steering occurs by controlling the articulation angle between the front and rear bodies. The state of the vehicle is defined as a four-element vector, [x y theta gamma], with the coordinates of the middle of the front axle, xy, specified in meters, the front body orientation, theta, and the articulation or steering angle, gamma, specified in radians. The articulation angle is defined as the front body steering relative to the rear body.

The MPPI controller runs at the block sample time. At each update, the controller samples control sequences, propagates them to generate potential trajectories, evaluates the trajectories with a cost function, and computes the optimal control command. For best performance, you must run the controller at a high frequency.

Examples

expand all

This example uses:

Open Live Script

This example demonstrates how to follow an obstacle-free path with an articulated steering vehicle model between two locations on a given map in Simulink®. It uses the RRT* planning algorithm to generate the path and Articulated Steering MPPI Controller block to generate control commands for navigating this path. It then simulates the vehicle motion based on those commands using the articulated steering kinematic model.

Load Occupancy Map

Load the occupancy map, which defines the map limits and obstacles within the environment. This example uses the offroadMap in the exampleHelperPlotMap function.

exampleHelperPlotMap();

The exampleHelperPlotMap function is a utility that loads an occupancy map from a .mat file, such as occupancyMapData.mat, creates a binaryOccupancyMap object, and visualizes it using the plot function. This visualization allows users and developers to verify the environment in which the robot will navigate.

Specify a start and end location within the map.

startLoc = [2 2];
goalLoc = [18 15];

Open Simulink Model

Open the Simulink model to understand its structure.

open_system('pathPlanningArticulatedMPPI.slx');

The model consists of three primary parts:

Planning: The Planner MATLAB Function block implements the RRT* algorithm. It takes the start location, goal location, and map as inputs, then outputs an array of waypoints that guide the vehicle to the goal position.

Path Following: This part consists of two key components:

  • Articulated Steering MPPI Controller: The Articulated Steering MPPI Controller generates the linear and angular velocity commands based on the waypoints and the current vehicle pose.

  • Has Reached Goal Flag: The HasReachedGoal flag, output by the Articulated Steering MPPI Controller block within the Solution Info bus, indicates whether the vehicle has successfully reached the goal. This example uses this flag to stop the simulation upon reaching the goal.

Plant: The Plant model simulates the simplified kinematics of the articulated steering vehicle model, applying the velocity commands to drive the system's motion toward the goal.

Visualize Vehicle Model

The Visualization block in the model displays the real-time motion of the vehicle as it navigates the map. It dynamically updates the vehicle's trajectory and position while overlaying the start and goal locations on the occupancy map. The visualization leverages helper functions, such as exampleHelperAnimateArticulatedVehicle and exampleHelperVehicleGeometry, to ensure accurate rendering of the vehicle's dimensions and movements.

Run the Simulink model to visualize the real-time motion of the vehicle.

simulation = sim('pathPlanningArticulatedMPPI.slx');

Ports

Input

expand all

Global xy-position, front body orientation, and steering angle of the vehicle, specified as a four-element vector in the form [x y theta gamma], that takes finite, real values. The global xy-position is specified in meters. The front body orientation, theta and articulation angle, gamma are specified in radians. The articulation angle is defined as the front body steering relative to the rear body.

Data Types: double

Current control commands of the vehicle, specified as a two-element vector that takes finite, real values.

For articulated steering vehicle model motion, the control commands are [v gammaDot]. v is the vehicle speed in the direction of motion in meters per second. gammaDot is the steering angle rate in radians per second.

Data Types: double | numeric

Reference path to follow, specified as an N-by-3 matrix in which each row represents a pose on the path.

Data Types: double | numeric

The vehicle speed range is a two-element vector that provides the minimum and maximum vehicle speeds, [MinSpeed MaxSpeed] in finite, real values, specified in meters per second.

Dependencies

To enable this port, select the Specify Vehicle Speed (m/s) Range from input port parameter on the Vehicle tab.

Data Types: double

The maximum steering rate of the front body relative to rear body, gammaDot, specified in radians per second. If the input steering rate goes beyond the maximum steering angle rate, it is limited to the maximum steering angle rate.

Dependencies

To enable this port, select the Specify Maximum Steering Rate (rad/s) from input port parameter on the Vehicle tab.

Data Types: double

Output

expand all

Optimal control commands of the vehicle, specified as a two-element numeric vector.

For articulated vehicle model motion, the control commands are [v gammaDot]. v is the vehicle velocity in the direction of motion in meters per second. gammaDot is the steering angle rate in radians per second.

Data Types: double

Optimal trajectory of the vehicle, returned as an N-by-4 matrix, where each row is in the form [x y θ γ].

N is the number of states along the trajectory. x is the current x-coordinate in meters. y is the current y-coordinate in meters. θ is the current front body orientation angle of the vehicle in radians. γ is the steering angle of the vehicle in radians. Each row of the matrix represents vehicle state along optimal trajectory.

Data Types: double

Extra information, returned as a scalar (bus) with these fields.

FieldDescription
HasReachedGoalIndicates whether the vehicle has successfully reached the last pose of the reference path within the goal tolerance, returned as true if successful. Otherwise, this value is false.
ExitFlag

Scalar value indicating the exit condition.

  • 0 — The control sequences and trajectories of the output are feasible.

  • 1 — The control sequences and trajectories of the output are not feasible due to constraint violations.

  • 2 — The next reference path pose is farther than what the vehicle can cover in the specified lookahead time while traveling at the maximum forward velocity of the vehicle model.

Data Types: bus

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

General

Configure various path-following parameters that guide the controller to make the vehicle accurately follow the desired path.

Path Following Parameters

Tolerance around the goal pose, specified as a three-element vector of the form [x y θ]. x and y denote the position of the robot in the x- and y-directions, respectively. Units are in meters. θ is the front body orientation angle of the vehicle in radians. This value specifies the maximum distance from the goal pose at which the planner can consider the robot to have reached the goal pose.

Lookahead time for trajectory planning in seconds, specified as a positive numeric scalar.

The vehicle model determines the maximum forward velocity of the vehicle. The lookahead time of the controller multiplied by the maximum forward velocity of the vehicle determines the lookahead distance of the controller.

The lookahead distance of the controller is the distance from the current pose of the vehicle for which the controller must optimize the local path. The lookahead distance determines the segment of the global reference path from the current pose that the controller considers for an iteration of local path planning. The reference path pose at a lookahead distance from the current pose is the lookahead point, and all reference path poses between the current pose and the lookahead point are lookahead poses.

Increasing the value of lookahead time causes the controller to generate controls further into the future, enabling the vehicle to react earlier to unseen obstacles at the cost of increased computation time. Conversely, a smaller lookahead time reduces the available time to react to new unknown obstacles, but enables the controller to run at a faster rate.

Block Parameters

Time interval at which the block updates during simulation in seconds, specified as a numeric value. Use a positive scalar for discrete execution, or -1 to inherit from upstream blocks. You must ensure consistency with other model components for optimal performance.

Specify the type of simulation to run.

  • Code generation — Simulate model using generated C code. The first time you run a simulation, Simulink generates C code for the block. The C code is reused for subsequent simulations, as long as the model does not change.

  • Interpreted execution — Simulate model using the MATLAB® interpreter. For more information, see Interpreted Execution vs. Code Generation (Simulink).

Tunable: No

Vehicle

Specify the vehicle specifications, limits, and other properties for a articulatedSteeringKinematics vehicle model.

Vehicle Specifications

The front angle offset refers to the length from the articulated joint to the front axle, specified in meters.

The rear angle offset refers to the length from the articulated joint to the rear axle, specified in meters.

The maximum steering angle of the front body relative to rear body, specified in radians.

Vehicle Limits

The vehicle speed range is a two-element vector that provides the minimum and maximum vehicle speeds, [MinSpeed MaxSpeed], specified in meters per second.

The maximum steering angle rate of the front body relative to rear body, gammaDot, specified in radians per second. If the input steering rate goes beyond the maximum steering angle rate, it is limited to the maximum steering angle rate.

Specify Vehicle Properties from Input Ports

Select this parameter to specify the speed range of the articulated steering vehicle model at the Vehicle Speed Range input port. Enabling this option removes the Vehicle Speed Range (m/s) parameter from the block mask.

Select this parameter to specify the maximum steering rate of the articulated steering vehicle model at the Max Steering Rate input port. Enabling this option removes the Maximum Steering Rate (rad/s) parameter from the block mask.

Controller

Specify various parameters for the MPPI Controller, which is used for motion planning of the bicycle vehicle model in the Articulated Steering MPPI Controller block.

Cost Weights

Weight for aligning with the lookahead poses of the reference path, specified as a nonnegative scalar.

Weight for closely following lookahead point, specified as a nonnegative scalar.

Weight for smoothing control actions to achieve optimal trajectory, specified as a nonnegative scalar.

Trajectory Generation Parameters

Number of sampled trajectories, specified as a positive integer.

The controller calculates the optimal trajectory by averaging the controls of candidate trajectories, with weights determined by their associated costs.

A larger number of trajectories can lead to a more thorough search of the trajectory space and a potentially better solution, at the cost of increased computation time.

Time between consecutive states of the trajectory in seconds, specified as a positive scalar. Smaller values lead to more precise trajectory predictions, but increased computation time.

Standard deviation for vehicle inputs, specified as a two-element numeric vector with nonnegative values. For the articulated steering vehicle model, the default value is [2 0.5].

Each element of the vector specifies the standard deviation for a control input of the vehicle model, such as steering or velocity. Each model has two control inputs. By introducing such variability into the control inputs during trajectory sampling, the controller can better explore different possible trajectories. Larger standard deviations enable the controller to account for uncertainties in the control input and achieve more realistic trajectory predictions.

Selectiveness of the optimal trajectory, specified as a positive scalar.

Specify a value close to 0 to favor the trajectory with the lowest cost as the optimal trajectory. Specify a larger value to favor the average of all sampled trajectories as the optimal trajectory.

This parameter adjusts the sensitivity of the MPPI algorithm to the cost differences, acting as a scaling factor that influences the weighting of candidate trajectories.

Extended Capabilities

expand all

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2025b

See Also

| |

Topics