Estimate Expected Shortfall for Asset Portfolios
This example shows how to compute the expected shortfall (ES) for a portfolio of equity positions using three different methods. ES is a market risk metric that supplements a calculated value-at-risk (VaR) value. For an example of ES computation on a single market index, see Expected Shortfall Estimation and Backtesting. The 95% VaR represents the threshold loss amount that is only violated about 5% of the time, while ES is an estimate of the average amount of money the portfolio loses on the 5% of days when the VaR is violated.
Because ES values are used as a supplement to a given VaR model, this example begins by calculating a set of VaR values. For a deeper discussion of VaR calculation on a portfolio of equity positions, see Estimate VaR for Equity Portfolio Using Parametric Methods. In this example, the VaR values are calculated using the Exponentially Weighted Moving Average (EWMA) approach discussed in Estimate VaR for Equity Portfolio Using Parametric Methods. Also, this example assumes that the portfolio returns are normally distributed.
VaR Calculation
To calculate a VaR, load the data, calculate the returns, and set the window variables for the rolling data window.
% Load equity prices equityPrices = load("SharePrices.mat","data"); equityPrices = equityPrices.data; returns = tick2ret(equityPrices); sampleSize = length(returns); windowSize = 250; testWindowSize = sampleSize-windowSize;
Load an equity portfolio to analyze. Then, calculate the dollar value of exposure to each stock.
% Load simulatd equity portfolio numShares = load("SimulatedRiskParityPortfolio.mat","RiskParityPortfolio"); numShares = numShares.RiskParityPortfolio; % Dollar value of exposure to each stock V = equityPrices(windowSize+1:end-1,:).*numShares;
Use norminv to find the z-score for the specified confidence level (95%) and initialize the VaR, , and profit and loss (P&L) vectors. (You use the and P&L vectors for backtesting in ES Backtest.)
% VaR confidence level pVaR = 0.95; zScore = norminv(pVaR); % Initialize VaR vector ewma95 = zeros(testWindowSize,1); % Initialize portfolioSigmas and P&L answer vectors ewmaPortfolioSigmas = zeros(testWindowSize,1); portfolioPandL = zeros(testWindowSize,1);
For each trading day, estimate VaR using the covariances of the returns, the amount invested in each asset, and the z-score for the confidence level. (For more information on this process, see Estimate VaR for Equity Portfolio Using Parametric Methods.) Also, save and P&L values for each day.
% t is the index number within the estimation window, % k is the index number within the entire data set. for t = 1:testWindowSize k = windowSize + t; % Calculate covariance Matrix covMatrixData = returns(t:k-1,:); % Using ewstats to compute exponentially weighted covariance matrix. lambda = 0.94; [~,ewmaCovMatrix] = ewstats(covMatrixData,lambda,windowSize); % Calculate the standard deviation of the portfolio returns. v = V(t,:); ewmaPortfolioSigmas(t) = sqrt(v*ewmaCovMatrix*v'); % Save VaR values ewma95(t) = zScore*ewmaPortfolioSigmas(t); % Save P&L values portfolioPandL(t) = sum(returns(k,:).*v); end
ES as VaR Average
An ES estimate is the probability-weighted average of tail losses and is calculated up from the VaR threshold. For example, given a 95% VaR for a portfolio, you must average the tail losses from the 95th–100th percentile to calculate the associated ES value. One way to estimate the ES for a given VaR value is to average a set of VaR values with a greater confidence level [2]. For this example, the 95% VaR is the primary VaR, but you can also calculate the VaR for the 95.5%, 96%, 96.5%, 97%, 97.5%, 98%, 98.5%, 99%, and 99.5% confidence levels. These other VaR values represent equally-spaced percentile estimates that fall above the 95% VaR level. Consequently, you can estimate the ES for the 95% VaR by averaging these higher VaR values.
Create a grid of confidence levels greater than 95%, then calculate the associated esZScores.
% VaR confidence levels for ES estimation
esPVaRs = [0.955, 0.96, 0.965, 0.97, 0.975, 0.98, 0.985, 0.99, 0.995];
esZScores = norminv(esPVaRs)esZScores = 1×9
1.6954 1.7507 1.8119 1.8808 1.9600 2.0537 2.1701 2.3263 2.5758
To calculate the new VaR values, multiply esZScores by the saved values.
esVaRValues = ewmaPortfolioSigmas*esZScores;
Average the computed VaR estimates using the mean function to get ES estimates.
esByVaRAverage = mean(esVaRValues,2);
ES as Average of Inverted Normal CDF Values
In the ES as VaR Average method, you calculate VaR estimates for different thresholds above 95% then estimate the portfolio distribution's tail average (the ES) by averaging the VaR values in the tail. Alternatively, you can recognize that the VaR values are derived from a normal probability distribution function (pdf), which means that you can then calculate what the VaR values are by inverting the cumulative distribution function (cdf) for the normal pdf that is defined by the VaR method. Consider the following cdf and pdf.
openfig("CombinedNormalCDFAndPDFInverse.fig",'new','visible');
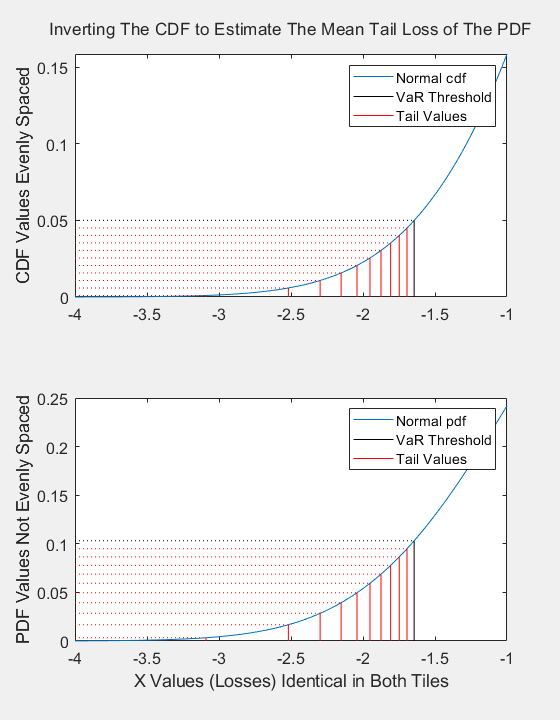
The ES is visualized as the probability-weighted integral of the left-tail of the portfolio returns pdf, or alternatively, the simple average of the left tail of the portfolio returns cdf. The top figure depicts the portfolio returns cdf with a selected set of evenly spaced y-values going from 0 to (where is the confidence level), in this case, from 0 to 0.05. You can invert the y-values to get a set of x-values, which represent portfolio returns (losses) over the relevant portion of the pdf. Because the y-values represent probability thresholds (and are evenly spaced), a simple average gives the probability-weighted average of the tail of the pdf. This is equivalent to calculating a set of equally spaced VaR values and averaging them.
The bottom figure depicts the portfolio returns pdf along with a set of y-values equivalent to the y-values in the top figure. These values are not evenly spaced, but if they were, a simple average of the x-values would not yield the probability-weighted average of the tail losses. Instead, you have to weight each x-value with a point estimate of the probability of the x value (an estimate of the area under the curve between the lines). However, because the specified y-values are spaced evenly in probability, a simple average yields the correct answer.
In these two figures, the cdf and pdf distributions assume a mean of 0, and a variance of 1. The VaR methodology also assumes a mean of 0 and the values for each day are saved in the vector ewmaPortfolioSigmas. Using this value, you can estimate the ES as an average of inverted Normal cdf values.
Create a grid of probabilities from 0 to 0.05. Invert the cdfs for each value, for each of the probabilities, using norminv. Average these values over the probabilities to get ES estimates.
p = .0001:.0001:.05; mu = 0; invertedNormValues = -norminv(p,mu,ewmaPortfolioSigmas); esByInvertedNormalCDF = mean(invertedNormValues,2);
Compute ES from Analytic Formula
The analytic formula for the case where the portfolio return distribution is normal is [1]
,
where is the mean portfolio return (assumed 0), is the standard deviation of the portfolio returns, is the confidence level (.95), is the probability distribution function (pdf) for the normal distribution, and is the cumulative distribution function (cdf) of the normal distribution. Compute ES estimates using this formula.
esByAnalyticFormula = -1*(mu-ewmaPortfolioSigmas*normpdf(norminv(pVaR))./(1-pVaR));
Plot Results for Three ES Methods
Plot the three sets of ES values versus trading day. The plots show that these values are similar with esByVaRAverage consistently coming in lowest. The VaR average uses only nine VaR values, which misses a larger fraction of the tail of the returns distribution than the other methods. Because the largest losses are farther along the tail, this results in a slightly lower ES estimate.
% Plot to compare different ES values X = 1:testWindowSize; f = figure; plot(X, esByVaRAverage, 'ks', X, esByInvertedNormalCDF, 'bo', X, esByAnalyticFormula,'r-'); legend({'ES from VaR Average','ES from Inverted Normal CDF','ES from Analytic Formula'},'Location','Best')

ES Backtest
Validating the ES values requires backtesting the computed ES sequence. In the Risk Management Toolbox™, you can do this using esbacktest or esbacktestbysim. For a discussion of the mathematics of ES backtesting, see Overview of Expected Shortfall Backtesting. To use esbacktest, pass the function the P&L values, VaR values, and ES values. Then use the summary and runtests functions with the resulting esbacktest object.
ebt = esbacktest(portfolioPandL,ewma95,esByAnalyticFormula,"VaRLevel",0.95);
summaryTable = summary(ebt)summaryTable=1×11 table
PortfolioID VaRID VaRLevel ObservedLevel ExpectedSeverity ObservedSeverity Observations Failures Expected Ratio Missing
___________ _____ ________ _____________ ________________ ________________ ____________ ________ ________ ______ _______
"Portfolio" "VaR" 0.95 0.9096 1.254 1.4181 531 48 26.55 1.8079 0
testsTable = runtests(ebt,"ShowDetails",true)testsTable=1×6 table
PortfolioID VaRID VaRLevel UnconditionalNormal UnconditionalT TestLevel
___________ _____ ________ ___________________ ______________ _________
"Portfolio" "VaR" 0.95 reject reject 0.95
The esbacktest function has two tests, the unconditional normal and t tests. esbacktest doesn't require any information about the portfolio return distribution, making it a flexible tool for evaluating ES performance, even for methods that do not assume an explicit form for the portfolio returns' distribution. However, for the same reason, esbacktest is also relatively limited in terms of accuracy.
In this case, the VaR and ES calculations leverage explicit distributional assumptions, and you compute parameters to match those assumptions. Consequently, it is best to use esbacktestbysim because this functionality runs a comprehensive suite of tests on the ES data. esbacktestbysim takes the same inputs as esbacktest, along with distribution information (currently, esbacktestbysim only supports normal, t, and empirical distributions). You can use esbacktestbysim to simulate a set of portfolio returns that you can compare against the actual portfolio and ES data using a variety of test metrics.
ebtSim = esbacktestbysim(portfolioPandL,ewma95,esByAnalyticFormula,"normal",'StandardDeviation',ewmaPortfolioSigmas,'mean',0,'VaRLevel',0.95); rng(1,"twister"); simSummary = summary(ebtSim)
simSummary=1×11 table
PortfolioID VaRID VaRLevel ObservedLevel ExpectedSeverity ObservedSeverity Observations Failures Expected Ratio Missing
___________ _____ ________ _____________ ________________ ________________ ____________ ________ ________ ______ _______
"Portfolio" "VaR" 0.95 0.9096 1.254 1.4181 531 48 26.55 1.8079 0
simTests = runtests(ebtSim,'ShowDetails',true)simTests=1×9 table
PortfolioID VaRID VaRLevel Conditional Unconditional Quantile MinBiasAbsolute MinBiasRelative TestLevel
___________ _____ ________ ___________ _____________ ________ _______________ _______________ _________
"Portfolio" "VaR" 0.95 reject reject reject reject reject 0.95
The computed ES values do not match the actual portfolio performance, suggesting the distribution assumptions are inadequate. The Estimate VaR for Equity Portfolio Using Parametric Methods has a similar result with the same portfolio, but with VaR backtesting instead of ES backtesting. The issue in both cases is the assumption that the portfolio returns are normally distributed, while actual financial data has fatter tails. Two possible alternatives are:
Use a different parametric method. Modeling the portfolio returns with a t-distribution, for example, results in fatter tails than with the normal distribution. You can use
tinvto get thezscoresand replace the standard deviation with a scale parameter, then proceed to compute the VaR and ES values. However, you do need to estimate the degrees of freedom for the t-distribution. Additionally, the analytic formula for computing the ES values has to change, as that formula is based on a normal distribution. For an example of an analytic ES calculation with a t-distribution, see Expected Shortfall Estimation and Backtesting. Alternatively, calculating the ES by averaging VaR values computed with a t distribution is essentially identical to the workflow in this example, as is calculating the ES by inverting the cdf for a t distribution (although you usetinvinstead ofnorminv).Use a nonparametric method to calculate the portfolio VaR and ES by using a historical VaR method. For an example of calculating a historical ES, see Expected Shortfall Estimation and Backtesting.
References
[1] McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton Series in Finance. Princeton, N.J: Princeton University Press, 2005.
[2] Dowd, Kevin. Measuring Market Risk. 1st ed. Wiley, 2005.
See Also
esbacktestbyde | esbacktest | esbacktestbysim | varbacktest
Topics
- VaR Backtesting Workflow
- Value-at-Risk Estimation and Backtesting
- Expected Shortfall (ES) Backtesting Workflow with No Model Distribution Information
- Expected Shortfall (ES) Backtesting Workflow Using Simulation
- Expected Shortfall Estimation and Backtesting
- Workflow for Expected Shortfall (ES) Backtesting by Du and Escanciano