Analyze and Plot RF Components
Analyze Networks in Frequency Domain
RF Toolbox™ lets you analyze RF components and networks in the frequency domain.
You use the analyze
function to analyze a circuit object over a specified set of frequencies.
For example, to analyze a coaxial transmission line from 1 GHz to 2.9 GHz in increments of 10 MHz:
ckt = rfckt.coaxial; f = [1.0e9:1e7:2.9e9]; analyze(ckt,f);
Note
For all circuits objects except those that contain data from a file, you must
perform a frequency-domain analysis with the analyze method before visualizing component and network data.
For circuits that contain data from a file, the toolbox performs a
frequency-domain analysis when you use the read method to import the
data.
When you analyze a circuit object, the toolbox computes the circuit network
parameters, noise figure values, and output third-order intercept point (OIP3)
values at the specified frequencies and stores the result of the analysis in the
object's AnalyzedResult property.
For more information, see the analyze
function page.
Visualize Component and Network Data
The RF Toolbox lets you validate the behavior of circuit objects that represent RF components and networks by plotting the following data:
Large- and small-signal S-parameters
Noise figure
Output third-order intercept point
Power data
Phase noise
Voltage standing-wave ratio
Power gain
Group delay
Reflection coefficients
Stability data
Transfer function
This table summarizes the available plots and charts, along with the functions you can use to create each one and a description of its contents.
| Plot Type | Functions | Plot Contents |
|---|---|---|
| Rectangular Plot | Parameters as a function of frequency or, where applicable, operating condition. The available parameters include:
| |
| Budget Plot | Parameters as a function of frequency for each component in a cascade, where the curve for a given component represents the cumulative contribution of each RF component up to and including the parameter value of that component. | |
| Mixer Spur Plot | Mixer spur power as a function of frequency for an
| |
| Polar Plots and Smith Charts | Polar plot: Magnitude and phase of S-parameters as a function of frequency. Smith plot: Real and imaginary parts of S-parameters as a function of frequency, used for analyzing the reflections caused by impedance mismatch. |
For each plot you create, you choose a parameter to plot and, optionally, a format in which to plot that parameter. The plot format defines how the RF Toolbox displays the data on the plot. The available formats vary with the data you select to plot. The data you can plot depends on the type of plot you create.
Note
You can use the listparam function to list the
parameters of a specified circuit object that are available for plotting. You
can use the listformat function to list the
available formats for a specified circuit object parameter.
The following topics describe the available plots:
Rectangular Plot
You can plot any parameters that are relevant to your object on a rectangular
plot. You can plot parameters as a function of frequency for any object. When
you import object data from a .p2d or .s2d
file, you can also plot parameters as a function of any operating condition from
the file that has numeric values, such as bias. In addition, when you import
object data from a .p2d file, you can plot large-signal
S-parameters as a function of input power or as a function of frequency. These
parameters are denoted LS11, LS12,
LS21, and LS22.
This table summarizes the methods that are available in the toolbox for creating rectangular plots and describes the uses of each one. For more information on a particular type of plot, follow the link in the table to the documentation for that method.
| Method | Description |
|---|---|
plot | Plot of one or more object parameters |
plotyy | Plot of one or more object parameters with y-axes on both the left and right sides |
semilogx | Plot of one or more object parameters using a log scale for the X-axis |
semilogy | Plot of one or more object parameters using a log scale for the Y-axis |
loglog | Plot of one or more object parameters using a log-log scale |
Budget Plot
You use the link budget or budget plot to understand the individual contribution of each component to a plotted parameter value in a cascaded network with multiple components. The budget plot shows one or more curves of parameter values as a function of frequency, ordered by the circuit index of the cascaded network.
Consider the following cascaded network:
casc = rfckt.cascade('Ckts',... {rfckt.amplifier,rfckt.lcbandpasspi,rfckt.txline})

You create a 3-D budget plot for this cascade using the
plot method with the second argument set to
'budget', as shown in the following
command:
analyze(casc,linspace(1e9,3e9,100)); plot(casc,'budget','s21')
Note that you have to analyze your circuit before plotting the budget plot and by
default the budget plot is a 2-D plot. If you specify the array of frequencies
in the analyze function you can visualize the budget
results in 3-D. A curve on the budget plot for each circuit index represents the
contributions to the parameter value of the RF components up to that index. This
figure shows the budget plot.

If you specify two or more parameters, the RF Toolbox puts the parameters in a single plot. You can only specify a single format for all the parameters.
Mixer Spur Plot
You use the mixer spur plot to understand how mixer nonlinearities affect output power at the desired mixer output frequency and at the intermodulation products that occur at the following frequencies:
where
is the input frequency.
is the local oscillator frequency.
N and M are integers.
The RF toolbox calculates the output power from the mixer intermodulation table (IMT). These tables are described in detail in the Visualize Mixer Spurs example.
The mixer spur plot shows power as a function of frequency for an rfckt.mixer object or an rfckt.cascade object that contains a mixer. By default, the plot
is three-dimensional and shows a stem plot of power as a function of frequency,
ordered by the circuit index of the object. You can create a two-dimensional
stem plot of power as a function of frequency for a single circuit index by
specifying the index in the mixer spur plot command.
Consider the following cascaded network:
FirstCkt = rfckt.amplifier('NetworkData', ... rfdata.network('Type', 'S', 'Freq', 2.1e9, ... 'Data', [0,0;10,0]), 'NoiseData', 0, 'NonlinearData', inf); SecondCkt = read(rfckt.mixer, 'samplespur1.s2d'); ThirdCkt = rfckt.lcbandpasstee('L', [97.21 3.66 97.21]*1e-9, ... 'C', [1.63 43.25 1.63]*1.0e-12); CascadedCkt = rfckt.cascade('Ckts', ... {FirstCkt, SecondCkt, ThirdCkt});
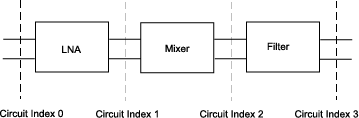
Circuit index 0 corresponds to the cascade input.
Circuit index 1 corresponds to the LNA output.
Circuit index 2 corresponds to the mixer output.
Circuit index 3 corresponds to the filter output.
You create a spur plot for this cascade using the plot
method with the second argument set to 'mixerspur', as shown
in the following
command:
plot(CascadedCkt,'mixerspur')
Within the three dimensional plot, the stem plot for each circuit index represents the power at that circuit index. This figure shows the mixer spur plot.
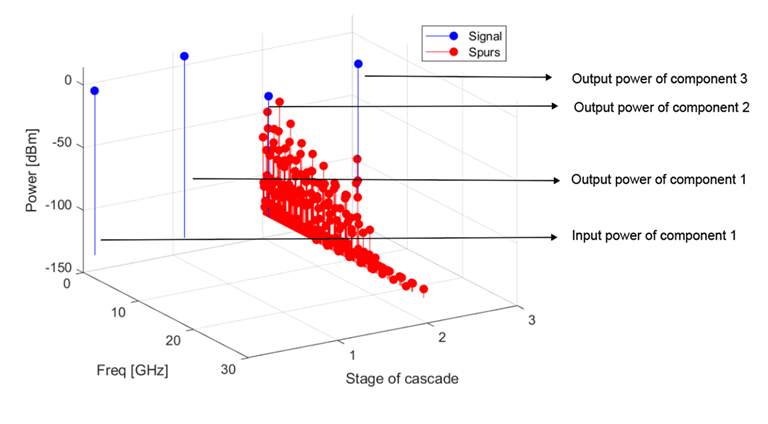
For more information on mixer spur plots, see the plot reference page.
Polar Plots and Smith Charts
You can use the RF toolbox to generate Polar plots and Smith charts. If you specify two or more parameters, the RF toolbox puts the parameters in a single plot.
The following table describes the Polar plot and Smith charts options, as well as the available parameters.
Note
LS11, LS12,
LS21, and LS22 are
large-signal S-parameters. You can plot these parameters as a function
of input power or as a function of frequency.
Plot Type | Method | Parameter |
|---|---|---|
| polar |
|
| smithplot with type argument
set to 'z' |
|
| smithplot with type argument
set to 'y' |
|
| smithplot with type argument
set to 'zy' |
|
By default, the RF toolbox plots the parameter as a function of frequency.
When you import block data from a .p2d or
.s2d file, you can also plot parameters as a function of
any operating condition from the file that has numeric values, such as
bias.
Note
The circle method lets you place circles on a Smith® Chart to depict stability regions and display constant gain, noise
figure, reflection and immittance circles. For more information about this
function, see the circle reference page or Designing Matching Networks for Low Noise Amplifiers example about designing matching
networks.
Compute and Plot Time-Domain Specifications
The RF toolbox lets you compute and plot time-domain characteristics for RF components.
This section contains the following topics:
Compute Network Transfer Function
You use the s2tf function to convert 2-port S-parameters
to a transfer function. The function returns a vector of transfer function
values that represent the normalized voltage gain of a 2-port network.
The following code illustrates how to read a file data into a passive circuit
object, extract the 2-port S-parameters from the object, and compute the
transfer function of the data at the frequencies for which the data is
specified. Here z0 is the reference impedance of the
S-parameters, zs is the source impedance, and
zl is the load impedance. See the s2tf reference page for more
information on how these impedances are used to define the gain.
PassiveCkt = rfckt.passive('File','passive.s2p') z0=50; zs=50; zl=50; [SParams, Freq] = extract(PassiveCkt, 'S Parameters', z0); TransFunc = s2tf(SParams, z0, zs, zl);
Fit Model Object to Circuit Object Data
You use the rationalfit function to fit a
rational function to the transfer function of a passive component. The
rationalfit function returns an
rfmodel object that represents the transfer function
analytically.
The following code illustrates how to use the rationalfit function to create an rfmodel.rational object that contains a rational function model of
the transfer function that you created in the previous example.
RationalFunc = rationalfit(Freq, TransFunc)
To find out how many poles the RF toolbox used to represent the data, look at
the length of the A vector of the
RationalFunc model object.
nPoles = length(RationalFunc.A)
Note
The number of poles is important if you plan to use the RF model object to create a model for use in another simulator, because a large number of poles can increase simulation time. For information on how to represent a component accurately using a minimum number of poles, see Represent Circuit Object with Model Object.
Use the freqresp function to compute the frequency response of the
fitted data. To validate the model fit, plot the transfer function of the
original data and the frequency response of the fitted data.
Resp = freqresp(RationalFunc, Freq); plot(Freq, 20*log10(abs(TransFunc)), 'r', ... Freq, 20*log10(abs(Resp)), 'b--'); ylabel('Magnitude of H(s) (decibels)'); xlabel('Frequency (Hz)'); legend('Original', 'Fitting result'); title(['Rational fitting with ', int2str(nPoles), ' poles']);
Compute and Plot Time-Domain Response
You use the timeresp function to compute the time-domain response of the
transfer function that RationalFunc represents. This code
illustrates how to create a random input signal, compute the time-domain
response of RationalFunc to the input signal, and plot the
results.
SampleTime=1e-11; NumberOfSamples=4750; OverSamplingFactor = 25; InputTime = double((1:NumberOfSamples)')*SampleTime; InputSignal = ... sign(randn(1, ceil(NumberOfSamples/OverSamplingFactor))); InputSignal = repmat(InputSignal, [OverSamplingFactor, 1]); InputSignal = InputSignal(:); [tresp,t]=timeresp(RationalFunc,InputSignal,SampleTime); plot(t*1e9,tresp); title('Fitting Time-Domain Response', 'fonts', 12); ylabel('Response to Random Input Signal'); xlabel('Time (ns)');
For more information about computing the time response of a model object, see
the timeresp function.