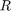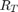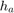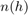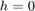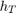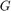slant2range
Syntax
Description
r = slant2range(sr,anht,tgtht)r between a target and sensor as a
function of the true target slant range sr, antenna height
anht, and target height tgtht. Propagated range
is the actual curved path range caused by atmospheric refraction. Slant range is the
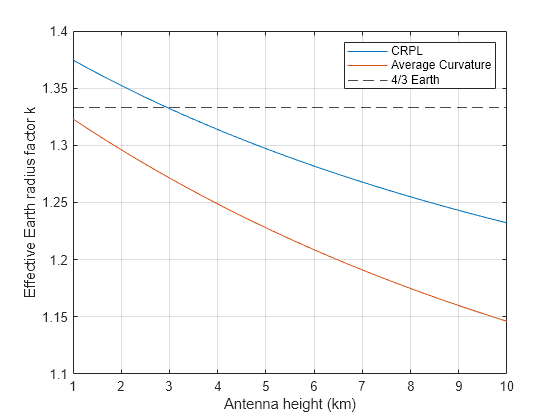
geometric range between target and sensor. The range computation assumes a Curved Earth Model where the atmospheric model is the
CRPL exponential reference atmosphere with a refractivity of 313 N-units and a refraction exponent
(decay constant) of 0.143859/km. The exponential atmosphere models refraction for elevation
angles greater than approximately 10 millirad (about 0.573 degrees) and heights above
approximately 1 km.
r = slant2range(sr,anht,tgtht,Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Barton, David K. Radar Equations for Modern Radar. Norwood, MA: Artech House, 2013.
[2] Bean, B.R., and G.D. Thayer. "Central Radio Propagation Laboratory Exponential Reference Atmosphere." Journal of Research of the National Bureau of Standards, Section D: Radio Propagation 63D, no. 3 (November 1959): 315. https://doi.org/10.6028/jres.063D.031.
[3] Blake, Lamont V. "Ray Height Computation for a Continuous Nonlinear Atmospheric Refractive-Index Profile." Radio Science 3, no. 1 (January 1968): 85–92. https://doi.org/10.1002/rds19683185.
Extended Capabilities
Version History
Introduced in R2022b