solve

Solve optimization problem or equation problem

Syntax

sol = solve(prob)

sol = solve(prob,x0)

sol = solve(prob,x0,ms)

sol = solve(___,Name,Value)

[sol,fval] = solve(___)

[sol,fval,exitflag,output,lambda] = solve(___)

Description

Use solve to find the solution of an optimization problem or equation problem.

Tip

For the full workflow, see Problem-Based Optimization Workflow or Problem-Based Workflow for Solving Equations.

sol = solve(prob) solves the optimization problem or equation problem prob.

sol = solve(prob,x0) solves prob starting from the point or set of values x0.

sol = solve(prob,x0,ms) solves prob using the ms multiple-start solver. Use this syntax to search for a better solution than you obtain when not using the ms argument.

sol = solve(___,Name,Value) modifies the solution process using one or more name-value pair arguments in addition to the input arguments in previous syntaxes.

[sol,fval] = solve(___) also returns the objective function value at the solution using any of the input arguments in previous syntaxes.

[sol,fval,exitflag,output,lambda] = solve(___) also returns an exit flag describing the exit condition, an output structure containing additional information about the solution process, and, for non-integer optimization problems, a Lagrange multiplier structure.

Examples

Solve Linear Programming Problem

Solve a linear programming problem defined by an optimization problem.

x = optimvar('x');
y = optimvar('y');
prob = optimproblem;
prob.Objective = -x - y/3;
prob.Constraints.cons1 = x + y <= 2;
prob.Constraints.cons2 = x + y/4 <= 1;
prob.Constraints.cons3 = x - y <= 2;
prob.Constraints.cons4 = x/4 + y >= -1;
prob.Constraints.cons5 = x + y >= 1;
prob.Constraints.cons6 = -x + y <= 2;

sol = solve(prob)

Solving problem using linprog.

Optimal solution found.

sol = struct with fields:
    x: 0.6667
    y: 1.3333

Solve Nonlinear Programming Problem Using Problem-Based Approach

Find a minimum of the peaks function, which is included in MATLAB®, in the region $$x^2+y^2\le 4$$. To do so, create optimization variables x and y.

x = optimvar('x');
y = optimvar('y');

Create an optimization problem having peaks as the objective function.

prob = optimproblem("Objective",peaks(x,y));

Include the constraint as an inequality in the optimization variables.

prob.Constraints = x^2 + y^2 <= 4;

Set the initial point for x to 1 and y to –1, and solve the problem.

x0.x = 1;
x0.y = -1;
sol = solve(prob,x0)

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol = struct with fields:
    x: 0.2283
    y: -1.6255

Unsupported Functions Require fcn2optimexpr

If your objective or nonlinear constraint functions are not entirely composed of elementary functions, you must convert the functions to optimization expressions using fcn2optimexpr. See Convert Nonlinear Function to Optimization Expression and Supported Operations for Optimization Variables and Expressions.

To convert the present example:

convpeaks = fcn2optimexpr(@peaks,x,y);
prob.Objective = convpeaks;
sol2 = solve(prob,x0)

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol2 = struct with fields:
    x: 0.2283
    y: -1.6255

Copyright 2018–2020 The MathWorks, Inc.

Solve Mixed-Integer Linear Program Starting from Initial Point

Compare the number of steps to solve an integer programming problem both with and without an initial feasible point. The problem has eight integer variables and four linear equality constraints, and all variables are restricted to be positive.

prob = optimproblem;
x = optimvar('x',8,1,'LowerBound',0,'Type','integer');

Create four linear equality constraints and include them in the problem.

Aeq = [22    13    26    33    21     3    14    26
    39    16    22    28    26    30    23    24
    18    14    29    27    30    38    26    26
    41    26    28    36    18    38    16    26];
beq = [ 7872
       10466
       11322
       12058];
cons = Aeq*x == beq;
prob.Constraints.cons = cons;

Create an objective function and include it in the problem.

f = [2    10    13    17     7     5     7     3];
prob.Objective = f*x;

Solve the problem without using an initial point, and examine the display to see the number of branch-and-bound nodes.

[x1,fval1,exitflag1,output1] = solve(prob);

Solving problem using intlinprog.
Running HiGHS 1.7.0: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [3e+00, 4e+01]
  Cost   [2e+00, 2e+01]
  Bound  [0e+00, 0e+00]
  RHS    [8e+03, 1e+04]
Presolving model
4 rows, 8 cols, 32 nonzeros  0s
4 rows, 8 cols, 27 nonzeros  0s
Objective function is integral with scale 1

Solving MIP model with:
   4 rows
   8 cols (0 binary, 8 integer, 0 implied int., 0 continuous)
   27 nonzeros

        Nodes      |    B&B Tree     |            Objective Bounds              |  Dynamic Constraints |       Work      
     Proc. InQueue |  Leaves   Expl. | BestBound       BestSol              Gap |   Cuts   InLp Confl. | LpIters     Time

         0       0         0   0.00%   0               inf                  inf        0      0      0         0     0.0s
         0       0         0   0.00%   1554.047531     inf                  inf        0      0      4         4     0.0s
 T   20753     210      8189  98.04%   1783.696925     1854               3.79%       30      8   9884     19222     3.0s

Solving report
  Status            Optimal
  Primal bound      1854
  Dual bound        1854
  Gap               0% (tolerance: 0.01%)
  Solution status   feasible
                    1854 (objective)
                    0 (bound viol.)
                    9.63673585375e-14 (int. viol.)
                    0 (row viol.)
  Timing            3.11 (total)
                    0.00 (presolve)
                    0.00 (postsolve)
  Nodes             21163
  LP iterations     19608 (total)
                    223 (strong br.)
                    76 (separation)
                    1018 (heuristics)

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

For comparison, find the solution using an initial feasible point.

x0.x = [8 62 23 103 53 84 46 34]';
[x2,fval2,exitflag2,output2] = solve(prob,x0);

Solving problem using intlinprog.
Running HiGHS 1.7.0: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [3e+00, 4e+01]
  Cost   [2e+00, 2e+01]
  Bound  [0e+00, 0e+00]
  RHS    [8e+03, 1e+04]
Assessing feasibility of MIP using primal feasibility and integrality tolerance of       1e-06
Solution has               num          max          sum
Col     infeasibilities      0            0            0
Integer infeasibilities      0            0            0
Row     infeasibilities      0            0            0
Row     residuals            0            0            0
Presolving model
4 rows, 8 cols, 32 nonzeros  0s
4 rows, 8 cols, 27 nonzeros  0s

MIP start solution is feasible, objective value is 3901
Objective function is integral with scale 1

Solving MIP model with:
   4 rows
   8 cols (0 binary, 8 integer, 0 implied int., 0 continuous)
   27 nonzeros

        Nodes      |    B&B Tree     |            Objective Bounds              |  Dynamic Constraints |       Work      
     Proc. InQueue |  Leaves   Expl. | BestBound       BestSol              Gap |   Cuts   InLp Confl. | LpIters     Time

         0       0         0   0.00%   0               3901             100.00%        0      0      0         0     0.0s
         0       0         0   0.00%   1554.047531     3901              60.16%        0      0      4         4     0.0s
 T    6266     708      2644  73.61%   1662.791423     3301              49.63%       20      6   9746     10699     1.5s
 T    9340     919      3970  80.72%   1692.410008     2687              37.01%       29      6   9995     16120     2.3s
 T   21750     192      9514  96.83%   1791.542628     1854               3.37%       20      6   9984     40278     5.8s

Solving report
  Status            Optimal
  Primal bound      1854
  Dual bound        1854
  Gap               0% (tolerance: 0.01%)
  Solution status   feasible
                    1854 (objective)
                    0 (bound viol.)
                    1.42108547152e-13 (int. viol.)
                    0 (row viol.)
  Timing            5.88 (total)
                    0.00 (presolve)
                    0.00 (postsolve)
  Nodes             22163
  LP iterations     40863 (total)
                    538 (strong br.)
                    64 (separation)
                    2782 (heuristics)

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

fprintf('Without an initial point, solve took %d steps.\nWith an initial point, solve took %d steps.',output1.numnodes,output2.numnodes)

Without an initial point, solve took 21163 steps.
With an initial point, solve took 22163 steps.

Giving an initial point does not always improve the problem. For this problem, using an initial point saves time and computational steps. However, for some problems, an initial point can cause solve to take more steps.

Specify Starting Points and Values for surrogateopt, Problem-Based

For some solvers, you can pass the objective and constraint function values, if any, to solve in the x0 argument. This can save time in the solver. Pass a vector of OptimizationValues objects. Create this vector using the optimvalues function.

The solvers that can use the objective function values are:

• ga

• gamultiobj

• paretosearch

• surrogateopt

The solvers that can use nonlinear constraint function values are:

• paretosearch

• surrogateopt

For example, minimize the peaks function using surrogateopt, starting with values from a grid of initial points. Create a grid from -10 to 10 in the x variable, and –5/2 to 5/2 in the y variable with spacing 1/2. Compute the objective function values at the initial points.

x = optimvar("x",LowerBound=-10,UpperBound=10);
y = optimvar("y",LowerBound=-5/2,UpperBound=5/2);
prob = optimproblem("Objective",peaks(x,y));
xval = -10:10;
yval = (-5:5)/2;
[x0x,x0y] = meshgrid(xval,yval);
peaksvals = peaks(x0x,x0y);

Pass the values in the x0 argument by using optimvalues. This saves time for solve, as solve does not need to compute the values. Pass the values as row vectors.

x0 = optimvalues(prob,'x',x0x(:)','y',x0y(:)',...
    "Objective",peaksvals(:)');

Solve the problem using surrogateopt with the initial values.

[sol,fval,eflag,output] = solve(prob,x0,Solver="surrogateopt")

Solving problem using surrogateopt.

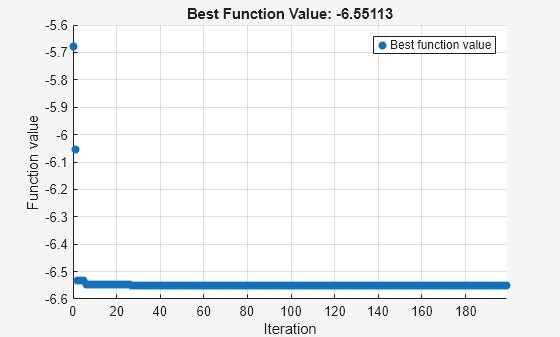
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
    x: 0.2279
    y: -1.6258

fval = 
-6.5511

eflag = 
    SolverLimitExceeded

output = struct with fields:
        elapsedtime: 19.2871
          funccount: 200
    constrviolation: 0
               ineq: [1x1 struct]
           rngstate: [1x1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'
             solver: 'surrogateopt'

Minimize Nonlinear Function Using Multiple-Start Solver, Problem-Based

Find a local minimum of the peaks function on the range $$-5\le x,y\le 5$$ starting from the point [–1,2].

x = optimvar("x",LowerBound=-5,UpperBound=5);
y = optimvar("y",LowerBound=-5,UpperBound=5);
x0.x = -1;
x0.y = 2;
prob = optimproblem(Objective=peaks(x,y));
opts = optimoptions("fmincon",Display="none");
[sol,fval] = solve(prob,x0,Options=opts)

sol = struct with fields:
    x: -3.3867
    y: 3.6341

fval = 
1.1224e-07

Try to find a better solution by using the GlobalSearch solver. This solver runs fmincon multiple times, which potentially yields a better solution.

ms = GlobalSearch;
[sol2,fval2] = solve(prob,x0,ms)

Solving problem using GlobalSearch.

GlobalSearch stopped because it analyzed all the trial points.

All 15 local solver runs converged with a positive local solver exit flag.

sol2 = struct with fields:
    x: 0.2283
    y: -1.6255

fval2 = 
-6.5511

GlobalSearch finds a solution with a better (lower) objective function value. The exit message shows that fmincon, the local solver, runs 15 times. The returned solution has an objective function value of about –6.5511, which is lower than the value at the first solution, 1.1224e–07.

Solve Integer Programming Problem with Nondefault Options

Solve the problem

$$\underset{x}{\min }\left(-3x_1-2x_2-x_3\right)subjectto\{\begin{array}{l}{x}_{3}binary\\ x_1,x_2\ge 0\\ x_1+x_2+x_3\le 7\\ 4x_1+2x_2+x_3=12\end{array}$$

without showing iterative display.

x = optimvar('x',2,1,'LowerBound',0);
x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1);
prob = optimproblem;
prob.Objective = -3*x(1) - 2*x(2) - x3;
prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7;
prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12;

options = optimoptions('intlinprog','Display','off');

sol = solve(prob,'Options',options)

sol = struct with fields:
     x: [2x1 double]
    x3: 0

Examine the solution.

sol.x

ans = 2×1

     0
     6

sol.x3

ans = 
0

Use intlinprog to Solve a Linear Program

Force solve to use intlinprog as the solver for a linear programming problem.

x = optimvar('x');
y = optimvar('y');
prob = optimproblem;
prob.Objective = -x - y/3;
prob.Constraints.cons1 = x + y <= 2;
prob.Constraints.cons2 = x + y/4 <= 1;
prob.Constraints.cons3 = x - y <= 2;
prob.Constraints.cons4 = x/4 + y >= -1;
prob.Constraints.cons5 = x + y >= 1;
prob.Constraints.cons6 = -x + y <= 2;

sol = solve(prob,'Solver', 'intlinprog')

Solving problem using intlinprog.
Running HiGHS 1.7.0: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [2e-01, 1e+00]
  Cost   [3e-01, 1e+00]
  Bound  [0e+00, 0e+00]
  RHS    [1e+00, 2e+00]
Presolving model
6 rows, 2 cols, 12 nonzeros  0s
4 rows, 2 cols, 8 nonzeros  0s
4 rows, 2 cols, 8 nonzeros  0s
Presolve : Reductions: rows 4(-2); columns 2(-0); elements 8(-4)
Solving the presolved LP
Using EKK dual simplex solver - serial
  Iteration        Objective     Infeasibilities num(sum)
          0    -1.3333333333e+03 Ph1: 3(4499); Du: 2(1.33333) 0s
          3    -1.1111111111e+00 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Simplex   iterations: 3
Objective value     : -1.1111111111e+00
HiGHS run time      :          0.00

Optimal solution found.

No integer variables specified. Intlinprog solved the linear problem.

sol = struct with fields:
    x: 0.6667
    y: 1.3333

Return All Outputs

Solve the mixed-integer linear programming problem described in Solve Integer Programming Problem with Nondefault Options and examine all of the output data.

x = optimvar('x',2,1,'LowerBound',0);
x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1);
prob = optimproblem;
prob.Objective = -3*x(1) - 2*x(2) - x3;
prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7;
prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12;

[sol,fval,exitflag,output] = solve(prob)

Solving problem using intlinprog.
Running HiGHS 1.7.0: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 4e+00]
  Cost   [1e+00, 3e+00]
  Bound  [1e+00, 1e+00]
  RHS    [7e+00, 1e+01]
Presolving model
2 rows, 3 cols, 6 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve: Optimal

Solving report
  Status            Optimal
  Primal bound      -12
  Dual bound        -12
  Gap               0% (tolerance: 0.01%)
  Solution status   feasible
                    -12 (objective)
                    0 (bound viol.)
                    0 (int. viol.)
                    0 (row viol.)
  Timing            0.00 (total)
                    0.00 (presolve)
                    0.00 (postsolve)
  Nodes             0
  LP iterations     0 (total)
                    0 (strong br.)
                    0 (separation)
                    0 (heuristics)

Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

sol = struct with fields:
     x: [2x1 double]
    x3: 0

fval = 
-12

exitflag = 
    OptimalSolution

output = struct with fields:
        relativegap: 0
        absolutegap: 0
      numfeaspoints: 0
           numnodes: 0
    constrviolation: 0
          algorithm: 'highs'
            message: 'Optimal solution found....'
             solver: 'intlinprog'

For a problem without any integer constraints, you can also obtain a nonempty Lagrange multiplier structure as the fifth output.

View Solution with Index Variables

Create and solve an optimization problem using named index variables. The problem is to maximize the profit-weighted flow of fruit to various airports, subject to constraints on the weighted flows.

rng(0) % For reproducibility
p = optimproblem('ObjectiveSense', 'maximize');
flow = optimvar('flow', ...
    {'apples', 'oranges', 'bananas', 'berries'}, {'NYC', 'BOS', 'LAX'}, ...
    'LowerBound',0,'Type','integer');
p.Objective = sum(sum(rand(4,3).*flow));
p.Constraints.NYC = rand(1,4)*flow(:,'NYC') <= 10;
p.Constraints.BOS = rand(1,4)*flow(:,'BOS') <= 12;
p.Constraints.LAX = rand(1,4)*flow(:,'LAX') <= 35;
sol = solve(p);

Solving problem using intlinprog.
Running HiGHS 1.7.0: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [4e-02, 1e+00]
  Cost   [1e-01, 1e+00]
  Bound  [0e+00, 0e+00]
  RHS    [1e+01, 4e+01]
Presolving model
3 rows, 12 cols, 12 nonzeros  0s
3 rows, 12 cols, 12 nonzeros  0s

Solving MIP model with:
   3 rows
   12 cols (0 binary, 12 integer, 0 implied int., 0 continuous)
   12 nonzeros

        Nodes      |    B&B Tree     |            Objective Bounds              |  Dynamic Constraints |       Work      
     Proc. InQueue |  Leaves   Expl. | BestBound       BestSol              Gap |   Cuts   InLp Confl. | LpIters     Time

         0       0         0   0.00%   1160.150059     -inf                 inf        0      0      0         0     0.0s
 S       0       0         0   0.00%   1160.150059     1027.233133       12.94%        0      0      0         0     0.0s

Solving report
  Status            Optimal
  Primal bound      1027.23313332
  Dual bound        1027.23313332
  Gap               0% (tolerance: 0.01%)
  Solution status   feasible
                    1027.23313332 (objective)
                    0 (bound viol.)
                    0 (int. viol.)
                    0 (row viol.)
  Timing            0.00 (total)
                    0.00 (presolve)
                    0.00 (postsolve)
  Nodes             1
  LP iterations     3 (total)
                    0 (strong br.)
                    0 (separation)
                    0 (heuristics)

Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

Find the optimal flow of oranges and berries to New York and Los Angeles.

[idxFruit,idxAirports] = findindex(flow, {'oranges','berries'}, {'NYC', 'LAX'})

idxFruit = 1×2

     2     4

idxAirports = 1×2

     1     3

orangeBerries = sol.flow(idxFruit, idxAirports)

orangeBerries = 2×2

     0   980
    70     0

This display means that no oranges are going to NYC, 70 berries are going to NYC, 980 oranges are going to LAX, and no berries are going to LAX.

List the optimal flow of the following:

Fruit Airports

----- --------

Berries NYC

Apples BOS

Oranges LAX

idx = findindex(flow, {'berries', 'apples', 'oranges'}, {'NYC', 'BOS', 'LAX'})

idx = 1×3

     4     5    10

optimalFlow = sol.flow(idx)

optimalFlow = 1×3

    70    28   980

This display means that 70 berries are going to NYC, 28 apples are going to BOS, and 980 oranges are going to LAX.

Solve Nonlinear System of Equations, Problem-Based

To solve the nonlinear system of equations

$$\begin{array}{l}\exp (-\exp (-(x_1+x_2)))=x_2(1+x_1^2)\\ x_1\cos (x_2)+x_2\sin (x_1)=\frac{1}{2}\end{array}$$

using the problem-based approach, first define x as a two-element optimization variable.

x = optimvar('x',2);

Create the first equation as an optimization equality expression.

eq1 = exp(-exp(-(x(1) + x(2)))) == x(2)*(1 + x(1)^2);

Similarly, create the second equation as an optimization equality expression.

eq2 = x(1)*cos(x(2)) + x(2)*sin(x(1)) == 1/2;

Create an equation problem, and place the equations in the problem.

prob = eqnproblem;
prob.Equations.eq1 = eq1;
prob.Equations.eq2 = eq2;

Review the problem.

show(prob)

  EquationProblem : 

	Solve for:
       x


 eq1:
       exp((-exp((-(x(1) + x(2)))))) == (x(2) .* (1 + x(1).^2))

 eq2:
       ((x(1) .* cos(x(2))) + (x(2) .* sin(x(1)))) == 0.5

Solve the problem starting from the point [0,0]. For the problem-based approach, specify the initial point as a structure, with the variable names as the fields of the structure. For this problem, there is only one variable, x.

x0.x = [0 0];
[sol,fval,exitflag] = solve(prob,x0)

Solving problem using fsolve.

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.

sol = struct with fields:
    x: [2x1 double]

fval = struct with fields:
    eq1: -2.4070e-07
    eq2: -3.8255e-08

exitflag = 
    EquationSolved

View the solution point.

disp(sol.x)

    0.3532
    0.6061

Unsupported Functions Require fcn2optimexpr

If your equation functions are not composed of elementary functions, you must convert the functions to optimization expressions using fcn2optimexpr. For the present example:

ls1 = fcn2optimexpr(@(x)exp(-exp(-(x(1)+x(2)))),x);
eq1 = ls1 == x(2)*(1 + x(1)^2);
ls2 = fcn2optimexpr(@(x)x(1)*cos(x(2))+x(2)*sin(x(1)),x);
eq2 = ls2 == 1/2;

See Supported Operations for Optimization Variables and Expressions and Convert Nonlinear Function to Optimization Expression.

Input Arguments

prob — Optimization problem or equation problem

OptimizationProblem object | EquationProblem object

Optimization problem or equation problem, specified as an OptimizationProblem object or an EquationProblem object. Create an optimization problem by using optimproblem; create an equation problem by using eqnproblem.

Warning

The problem-based approach does not support complex values in the following: an objective function, nonlinear equalities, and nonlinear inequalities. If a function calculation has a complex value, even as an intermediate value, the final result might be incorrect.

Example: prob = optimproblem; prob.Objective = obj; prob.Constraints.cons1 = cons1;

Example: prob = eqnproblem; prob.Equations = eqs;

x0 — Initial point

structure | vector of OptimizationValues objects

Initial point, specified as a structure with field names equal to the variable names in prob.

For some Global Optimization Toolbox solvers, x0 can be a vector of OptimizationValues objects representing multiple initial points. Create the points using the optimvalues function. These solvers are:

• ga (Global Optimization Toolbox), gamultiobj (Global Optimization Toolbox), paretosearch (Global Optimization Toolbox) and particleswarm (Global Optimization Toolbox). These solvers accept multiple starting points as members of the initial population.

• MultiStart (Global Optimization Toolbox). This solver accepts multiple initial points for a local solver such as fmincon.

• surrogateopt (Global Optimization Toolbox). This solver accepts multiple initial points to help create an initial surrogate.

For an example using x0 with named index variables, see Create Initial Point for Optimization with Named Index Variables.

Example: If prob has variables named x and y: x0.x = [3,2,17]; x0.y = [pi/3,2*pi/3].

Data Types: struct

ms — Multiple start solver

MultiStart object | GlobalSearch object

Multiple start solver, specified as a MultiStart (Global Optimization Toolbox) object or a GlobalSearch (Global Optimization Toolbox) object. Create ms using the MultiStart or GlobalSearch commands.

Currently, GlobalSearch supports only the fmincon local solver, and MultiStart supports only the fmincon, fminunc, and lsqnonlin local solvers.

Example: ms = MultiStart;

Example: ms = GlobalSearch(FunctionTolerance=1e-4);

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: solve(prob,'Options',opts)

MinNumStartPoints — Minimum number of start points for MultiStart

20 (default) | positive integer

Minimum number of start points for MultiStart (Global Optimization Toolbox), specified as a positive integer. This argument applies only when you call solve using the ms argument. solve uses all of the values in x0 as start points. If MinNumStartPoints is greater than the number of values in x0, then solve generates more start points uniformly at random within the problem bounds. If a component is unbounded, solve generates points using the default artificial bounds for MultiStart.

Example: solve(prob,x0,ms,MinNumStartPoints=50)

Data Types: double

Options — Optimization options

object created by optimoptions | options structure

Optimization options, specified as an object created by optimoptions or an options structure such as created by optimset.

Internally, the solve function calls a relevant solver as detailed in the 'solver' argument reference. Ensure that options is compatible with the solver. For example, intlinprog does not allow options to be a structure, and lsqnonneg does not allow options to be an object.

For suggestions on options settings to improve an intlinprog solution or the speed of a solution, see Tuning Integer Linear Programming. For linprog, the default 'dual-simplex' algorithm is generally memory-efficient and speedy. Occasionally, linprog solves a large problem faster when the Algorithm option is 'interior-point'. For suggestions on options settings to improve a nonlinear problem's solution, see Optimization Options in Common Use: Tuning and Troubleshooting and Improve Results.

Example: options = optimoptions('intlinprog','Display','none')

Solver — Optimization solver

'intlinprog' | 'linprog' | 'lsqlin' | 'lsqcurvefit' | 'lsqnonlin' | 'lsqnonneg' | 'quadprog' | 'fminbnd' | 'fminunc' | 'fmincon' | 'fminsearch' | 'fzero' | 'fsolve' | 'coneprog' | 'ga' | 'gamultiobj' | 'paretosearch' | 'patternsearch' | 'particleswarm' | 'surrogateopt' | 'simulannealbnd'

Optimization solver, specified as the name of a listed solver. For optimization problems, this table contains the available solvers for each problem type, including solvers from Global Optimization Toolbox. Details for equation problems appear below the optimization solver details.

For converting nonlinear problems with integer constraints using prob2struct, the resulting problem structure can depend on the chosen solver. If you do not have a Global Optimization Toolbox license, you must specify the solver. See Integer Constraints in Nonlinear Problem-Based Optimization.

The default solver for each optimization problem type is listed here.

Problem Type	Default Solver
Linear Programming (LP)	linprog
Mixed-Integer Linear Programming (MILP)	intlinprog
Quadratic Programming (QP)	quadprog
Second-Order Cone Programming (SOCP)	coneprog
Linear Least Squares	lsqlin
Nonlinear Least Squares	lsqnonlin
Nonlinear Programming (NLP)	fminunc for problems with no constraints, otherwise fmincon
Mixed-Integer Nonlinear Programming (MINLP)	ga (Global Optimization Toolbox)
Multiobjective	gamultiobj (Global Optimization Toolbox)

In this table, means the solver is available for the problem type, x means the solver is not available.

Problem Type	LP	MILP	QP	SOCP	Linear Least Squares	Nonlinear Least Squares	NLP	MINLP
Solver
linprog		x	x	x	x	x	x	x
intlinprog			x	x	x	x	x	x
quadprog		x				x	x	x
coneprog		x	x		x	x	x	x
lsqlin	x	x	x	x		x	x	x
lsqnonneg	x	x	x	x		x	x	x
lsqnonlin	x	x	x	x			x	x
fminunc		x		x				x
fmincon		x						x
fminbnd	x	x	x	x				x
fminsearch	x	x	x	x				x
patternsearch (Global Optimization Toolbox)		x						x
ga (Global Optimization Toolbox)
particleswarm (Global Optimization Toolbox)		x		x				x
simulannealbnd (Global Optimization Toolbox)		x		x				x
surrogateopt (Global Optimization Toolbox)
gamultiobj (Global Optimization Toolbox)
paretosearch (Global Optimization Toolbox)		x						x

Note

If you choose lsqcurvefit as the solver for a least-squares problem, solve uses lsqnonlin. The lsqcurvefit and lsqnonlin solvers are identical for solve.

Caution

For maximization problems (prob.ObjectiveSense is "max" or "maximize"), do not specify a least-squares solver (one with a name beginning lsq). If you do, solve throws an error, because these solvers cannot maximize.

For equation solving, this table contains the available solvers for each problem type. In the table,

• * indicates the default solver for the problem type.

• Y indicates an available solver.

• N indicates an unavailable solver.

Supported Solvers for Equations

Equation Type	lsqlin	lsqnonneg	fzero	fsolve	lsqnonlin
Linear	*	N	Y (scalar only)	Y	Y
Linear plus bounds	*	Y	N	N	Y
Scalar nonlinear	N	N	*	Y	Y
Nonlinear system	N	N	N	*	Y
Nonlinear system plus bounds	N	N	N	N	*

Example: 'intlinprog'

Data Types: char | string

ObjectiveDerivative — Indication to use automatic differentiation for objective function

'auto' (default) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

Indication to use automatic differentiation (AD) for nonlinear objective function, specified as 'auto' (use AD if possible), 'auto-forward' (use forward AD if possible), 'auto-reverse' (use reverse AD if possible), or 'finite-differences' (do not use AD). Choices including auto cause the underlying solver to use gradient information when solving the problem provided that the objective function is supported, as described in Supported Operations for Optimization Variables and Expressions. For an example, see Effect of Automatic Differentiation in Problem-Based Optimization.

Solvers choose the following type of AD by default:

• For a general nonlinear objective function, fmincon defaults to reverse AD for the objective function. fmincon defaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise, fmincon defaults to forward AD for the nonlinear constraint function.

• For a general nonlinear objective function, fminunc defaults to reverse AD.

• For a least-squares objective function, fmincon and fminunc default to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.

• lsqnonlin defaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise, lsqnonlin defaults to reverse AD.

• fsolve defaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise, fsolve defaults to reverse AD.

Example: 'finite-differences'

Data Types: char | string

ConstraintDerivative — Indication to use automatic differentiation for constraint functions

'auto' (default) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

Indication to use automatic differentiation (AD) for nonlinear constraint functions, specified as 'auto' (use AD if possible), 'auto-forward' (use forward AD if possible), 'auto-reverse' (use reverse AD if possible), or 'finite-differences' (do not use AD). Choices including auto cause the underlying solver to use gradient information when solving the problem provided that the constraint functions are supported, as described in Supported Operations for Optimization Variables and Expressions. For an example, see Effect of Automatic Differentiation in Problem-Based Optimization.

Solvers choose the following type of AD by default:

• For a general nonlinear objective function, fmincon defaults to reverse AD for the objective function. fmincon defaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise, fmincon defaults to forward AD for the nonlinear constraint function.

• For a general nonlinear objective function, fminunc defaults to reverse AD.

• For a least-squares objective function, fmincon and fminunc default to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.

• lsqnonlin defaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise, lsqnonlin defaults to reverse AD.

• fsolve defaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise, fsolve defaults to reverse AD.

Example: 'finite-differences'

Data Types: char | string

EquationDerivative — Indication to use automatic differentiation for equations

'auto' (default) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

Indication to use automatic differentiation (AD) for nonlinear constraint functions, specified as 'auto' (use AD if possible), 'auto-forward' (use forward AD if possible), 'auto-reverse' (use reverse AD if possible), or 'finite-differences' (do not use AD). Choices including auto cause the underlying solver to use gradient information when solving the problem provided that the equation functions are supported, as described in Supported Operations for Optimization Variables and Expressions. For an example, see Effect of Automatic Differentiation in Problem-Based Optimization.

Solvers choose the following type of AD by default:

• For a general nonlinear objective function, fmincon defaults to reverse AD for the objective function. fmincon defaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise, fmincon defaults to forward AD for the nonlinear constraint function.

• For a general nonlinear objective function, fminunc defaults to reverse AD.

• For a least-squares objective function, fmincon and fminunc default to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.

• lsqnonlin defaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise, lsqnonlin defaults to reverse AD.

• fsolve defaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise, fsolve defaults to reverse AD.

Example: 'finite-differences'

Data Types: char | string

Output Arguments

sol — Solution

structure | OptimizationValues vector

Solution, returned as a structure or an OptimizationValues vector. sol is an OptimizationValues vector when the problem is multiobjective. For single-objective problems, the fields of the returned structure are the names of the optimization variables in the problem. See optimvar.

fval — Objective function value at the solution

real number | real vector | real matrix | structure

Objective function value at the solution, returned as one of the following:

Problem Type	Returned Value(s)
Optimize scalar objective function f(x)	Real number f(sol)
Least squares	Real number, the sum of squares of the residuals at the solution
Solve equation	If prob.Equations is a single entry: Real vector of function values at the solution, meaning the left side minus the right side of the equations
	If prob.Equations has multiple named fields: Structure with same names as prob.Equations, where each field value is the left side minus the right side of the named equations
Multiobjective	Matrix with one row for each objective function component, and one column for each solution point.

Tip

If you neglect to ask for fval for an objective defined as an optimization expression or equation expression, you can calculate it using

fval = evaluate(prob.Objective,sol)

If the objective is defined as a structure with only one field,

fval = evaluate(prob.Objective.ObjectiveName,sol)

If the objective is a structure with multiple fields, write a loop.

fnames = fields(prob.Equations);
for i = 1:length(fnames)
    fval.(fnames{i}) = evaluate(prob.Equations.(fnames{i}),sol);
end

exitflag — Reason solver stopped

enumeration variable

Reason the solver stopped, returned as an enumeration variable. You can convert exitflag to its numeric equivalent using double(exitflag), and to its string equivalent using string(exitflag).

This table describes the exit flags for the intlinprog solver.

Exit Flag for intlinprog	Numeric Equivalent	Meaning
OptimalWithPoorFeasibility	3	The solution is feasible with respect to the relative ConstraintTolerance tolerance, but is not feasible with respect to the absolute tolerance.
IntegerFeasible	2	intlinprog stopped prematurely, and found an integer feasible point.
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	intlinprog exceeds one of the following tolerances: LPMaxIterations MaxNodes MaxTime RootLPMaxIterations See Tolerances and Stopping Criteria. solve also returns this exit flag when it runs out of memory at the root node.
OutputFcnStop	-1	intlinprog stopped by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point found.
Unbounded	-3	The problem is unbounded.
FeasibilityLost	-9	Solver lost feasibility.

Exitflags 3 and -9 relate to solutions that have large infeasibilities. These usually arise from linear constraint matrices that have large condition number, or problems that have large solution components. To correct these issues, try to scale the coefficient matrices, eliminate redundant linear constraints, or give tighter bounds on the variables.

This table describes the exit flags for the linprog solver.

Exit Flag for linprog	Numeric Equivalent	Meaning
OptimalWithPoorFeasibility	3	The solution is feasible with respect to the relative ConstraintTolerance tolerance, but is not feasible with respect to the absolute tolerance.
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	The number of iterations exceeds options.MaxIterations.
NoFeasiblePointFound	-2	No feasible point found.
Unbounded	-3	The problem is unbounded.
FoundNaN	-4	NaN value encountered during execution of the algorithm.
PrimalDualInfeasible	-5	Both primal and dual problems are infeasible.
DirectionTooSmall	-7	The search direction is too small. No further progress can be made.
FeasibilityLost	-9	Solver lost feasibility.

Exitflags 3 and -9 relate to solutions that have large infeasibilities. These usually arise from linear constraint matrices that have large condition number, or problems that have large solution components. To correct these issues, try to scale the coefficient matrices, eliminate redundant linear constraints, or give tighter bounds on the variables.

This table describes the exit flags for the lsqlin solver.

Exit Flag for lsqlin	Numeric Equivalent	Meaning
FunctionChangeBelowTolerance	3	Change in the residual is smaller than the specified tolerance options.FunctionTolerance. (trust-region-reflective algorithm)
StepSizeBelowTolerance	2	Step size smaller than options.StepTolerance, constraints satisfied. (interior-point algorithm)
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	The number of iterations exceeds options.MaxIterations.
NoFeasiblePointFound	-2	For optimization problems, the problem is infeasible. Or, for the interior-point algorithm, step size smaller than options.StepTolerance, but constraints are not satisfied. For equation problems, no solution found.
IllConditioned	-4	Ill-conditioning prevents further optimization.
NoDescentDirectionFound	-8	The search direction is too small. No further progress can be made. (interior-point algorithm)

This table describes the exit flags for the quadprog solver.

Exit Flag for quadprog	Numeric Equivalent	Meaning
LocalMinimumFound	4	Local minimum found; minimum is not unique.
FunctionChangeBelowTolerance	3	Change in the objective function value is smaller than the specified tolerance options.FunctionTolerance. (trust-region-reflective algorithm)
StepSizeBelowTolerance	2	Step size smaller than options.StepTolerance, constraints satisfied. (interior-point-convex algorithm)
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	The number of iterations exceeds options.MaxIterations.
NoFeasiblePointFound	-2	The problem is infeasible. Or, for the interior-point algorithm, step size smaller than options.StepTolerance, but constraints are not satisfied.
IllConditioned	-4	Ill-conditioning prevents further optimization.
Nonconvex	-6	Nonconvex problem detected. (interior-point-convex algorithm)
NoDescentDirectionFound	-8	Unable to compute a step direction. (interior-point-convex algorithm)

This table describes the exit flags for the coneprog solver.

Exit Flag for coneprog	Numeric Equivalent	Meaning
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	The number of iterations exceeds options.MaxIterations, or the solution time in seconds exceeded options.MaxTime.
NoFeasiblePointFound	-2	The problem is infeasible.
Unbounded	-3	The problem is unbounded.
DirectionTooSmall	-7	The search direction became too small. No further progress could be made.
Unstable	-10	The problem is numerically unstable.

This table describes the exit flags for the lsqcurvefit or lsqnonlin solver.

Exit Flag for lsqnonlin	Numeric Equivalent	Meaning
SearchDirectionTooSmall	4	Magnitude of search direction was smaller than options.StepTolerance.
FunctionChangeBelowTolerance	3	Change in the residual was less than options.FunctionTolerance.
StepSizeBelowTolerance	2	Step size smaller than options.StepTolerance.
OptimalSolution	1	The solver converged to a solution x.
SolverLimitExceeded	0	Number of iterations exceeded options.MaxIterations or number of function evaluations exceeded options.MaxFunctionEvaluations.
OutputFcnStop	-1	Stopped by an output function or plot function.
NoFeasiblePointFound	-2	For optimization problems, problem is infeasible: the bounds lb and ub are inconsistent. For equation problems, no solution found.

This table describes the exit flags for the fminunc solver.

Exit Flag for fminunc	Numeric Equivalent	Meaning
NoDecreaseAlongSearchDirection	5	Predicted decrease in the objective function is less than the options.FunctionTolerance tolerance.
FunctionChangeBelowTolerance	3	Change in the objective function value is less than the options.FunctionTolerance tolerance.
StepSizeBelowTolerance	2	Change in x is smaller than the options.StepTolerance tolerance.
OptimalSolution	1	Magnitude of gradient is smaller than the options.OptimalityTolerance tolerance.
SolverLimitExceeded	0	Number of iterations exceeds options.MaxIterations or number of function evaluations exceeds options.MaxFunctionEvaluations.
OutputFcnStop	-1	Stopped by an output function or plot function.
Unbounded	-3	Objective function at current iteration is below options.ObjectiveLimit.

This table describes the exit flags for the fmincon solver.

Exit Flag for fmincon	Numeric Equivalent	Meaning
NoDecreaseAlongSearchDirection	5	Magnitude of directional derivative in search direction is less than 2*options.OptimalityTolerance and maximum constraint violation is less than options.ConstraintTolerance.
SearchDirectionTooSmall	4	Magnitude of the search direction is less than 2*options.StepTolerance and maximum constraint violation is less than options.ConstraintTolerance.
FunctionChangeBelowTolerance	3	Change in the objective function value is less than options.FunctionTolerance and maximum constraint violation is less than options.ConstraintTolerance.
StepSizeBelowTolerance	2	Change in x is less than options.StepTolerance and maximum constraint violation is less than options.ConstraintTolerance.
OptimalSolution	1	First-order optimality measure is less than options.OptimalityTolerance, and maximum constraint violation is less than options.ConstraintTolerance.
SolverLimitExceeded	0	Number of iterations exceeds options.MaxIterations or number of function evaluations exceeds options.MaxFunctionEvaluations.
OutputFcnStop	-1	Stopped by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point found.
Unbounded	-3	Objective function at current iteration is below options.ObjectiveLimit and maximum constraint violation is less than options.ConstraintTolerance.

This table describes the exit flags for the fsolve solver.

Exit Flag for fsolve	Numeric Equivalent	Meaning
SearchDirectionTooSmall	4	Magnitude of the search direction is less than options.StepTolerance, equation solved.
FunctionChangeBelowTolerance	3	Change in the objective function value is less than options.FunctionTolerance, equation solved.
StepSizeBelowTolerance	2	Change in x is less than options.StepTolerance, equation solved.
OptimalSolution	1	First-order optimality measure is less than options.OptimalityTolerance, equation solved.
SolverLimitExceeded	0	Number of iterations exceeds options.MaxIterations or number of function evaluations exceeds options.MaxFunctionEvaluations.
OutputFcnStop	-1	Stopped by an output function or plot function.
NoFeasiblePointFound	-2	Converged to a point that is not a root.
TrustRegionRadiusTooSmall	-3	Equation not solved. Trust region radius became too small (trust-region-dogleg algorithm).

This table describes the exit flags for the fzero solver.

Exit Flag for fzero	Numeric Equivalent	Meaning
OptimalSolution	1	Equation solved.
OutputFcnStop	-1	Stopped by an output function or plot function.
FoundNaNInfOrComplex	-4	NaN, Inf, or complex value encountered during search for an interval containing a sign change.
SingularPoint	-5	Might have converged to a singular point.
CannotDetectSignChange	-6	Did not find two points with opposite signs of function value.

This table describes the exit flags for the patternsearch solver.

Exit Flag for patternsearch	Numeric Equivalent	Meaning
SearchDirectionTooSmall	4	The magnitude of the step is smaller than machine precision, and the constraint violation is less than ConstraintTolerance.
FunctionChangeBelowTolerance	3	The change in fval and the mesh size are both less than the specified tolerance, and the constraint violation is less than ConstraintTolerance.
StepSizeBelowTolerance	2	Change in x and the mesh size are both smaller than StepTolerance, and the constraint violation is less than ConstraintTolerance.
SolverConvergedSuccessfully	1	Without nonlinear constraints — The magnitude of the mesh size is less than the specified tolerance, and the constraint violation is less than ConstraintTolerance.
		With nonlinear constraints — The magnitude of the complementarity measure (defined after this table) is less than sqrt(ConstraintTolerance), the subproblem is solved using a mesh finer than MeshTolerance, and the constraint violation is less than ConstraintTolerance.
SolverLimitExceeded	0	The maximum number of function evaluations or iterations is reached.
OutputFcnStop	-1	Stopped by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point found.

In the nonlinear constraint solver, the complementarity measure is the norm of the vector whose elements are c_iλ_i, where c_i is the nonlinear inequality constraint violation, and λ_i is the corresponding Lagrange multiplier.

This table describes the exit flags for the ga solver.

Exit Flag for ga	Numeric Equivalent	Meaning
MinimumFitnessLimitReached	5	Minimum fitness limit FitnessLimit reached and the constraint violation is less than ConstraintTolerance.
SearchDirectionTooSmall	4	The magnitude of the step is smaller than machine precision, and the constraint violation is less than ConstraintTolerance.
FunctionChangeBelowTolerance	3	Value of the fitness function did not change in MaxStallGenerations generations and the constraint violation is less than ConstraintTolerance.
SolverConvergedSuccessfully	1	Without nonlinear constraints — Average cumulative change in value of the fitness function over MaxStallGenerations generations is less than FunctionTolerance, and the constraint violation is less than ConstraintTolerance.
		With nonlinear constraints — Magnitude of the complementarity measure (see Complementarity Measure (Global Optimization Toolbox)) is less than sqrt(ConstraintTolerance), the subproblem is solved using a tolerance less than FunctionTolerance, and the constraint violation is less than ConstraintTolerance.
SolverLimitExceeded	0	Maximum number of generations MaxGenerations exceeded.
OutputFcnStop	-1	Stopped by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point found.
StallTimeLimitExceeded	-4	Stall time limit MaxStallTime exceeded.
TimeLimitExceeded	-5	Time limit MaxTime exceeded.

This table describes the exit flags for the particleswarm solver.

Exit Flag for particleswarm	Numeric Equivalent	Meaning
SolverConvergedSuccessfully	1	Relative change in the objective value over the last options.MaxStallIterations iterations is less than options.FunctionTolerance.
SolverLimitExceeded	0	Number of iterations exceeded options.MaxIterations.
OutputFcnStop	-1	Iterations stopped by output function or plot function.
NoFeasiblePointFound	-2	Bounds are inconsistent: for some i, lb(i) > ub(i).
Unbounded	-3	Best objective function value is below options.ObjectiveLimit.
StallTimeLimitExceeded	-4	Best objective function value did not change within options.MaxStallTime seconds.
TimeLimitExceeded	-5	Run time exceeded options.MaxTime seconds.

This table describes the exit flags for the simulannealbnd solver.

Exit Flag for simulannealbnd	Numeric Equivalent	Meaning
ObjectiveValueBelowLimit	5	Objective function value is less than options.ObjectiveLimit.
SolverConvergedSuccessfully	1	Average change in the value of the objective function over options.MaxStallIterations iterations is less than options.FunctionTolerance.
SolverLimitExceeded	0	Maximum number of generations MaxGenerations exceeded.
OutputFcnStop	-1	Optimization terminated by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point found.
TimeLimitExceeded	-5	Time limit exceeded.

This table describes the exit flags for the surrogateopt solver.

Exit Flag for surrogateopt	Numeric Equivalent	Meaning
BoundsEqual	10	Problem has a unique feasible solution due to one of the following: All upper bounds ub (Global Optimization Toolbox) are equal to the lower bounds lb (Global Optimization Toolbox). The linear equality constraints Aeq*x = beq and the bounds have a unique solution point. surrogateopt returns the feasible point and function value without performing any optimization.
FeasiblePointFound	3	Feasible point found. Solver stopped because too few new feasible points were found to continue.
ObjectiveLimitAttained	1	The objective function value is less than options.ObjectiveLimit. This exit flag takes precedence over exit flag 10 when both apply.
SolverLimitExceeded	0	The number of function evaluations exceeds options.MaxFunctionEvaluations or the elapsed time exceeds options.MaxTime. If the problem has nonlinear inequalities, the solution is feasible.
OutputFcnStop	-1	The optimization is terminated by an output function or plot function.
NoFeasiblePointFound	-2	No feasible point is found due to one of the following: A lower bound lb(i) exceeds a corresponding upper bound ub(i). Or one or more ceil(lb(i)) exceeds a corresponding floor(ub(i)) for i in intcon (Global Optimization Toolbox). In this case, solve returns x = [] and fval = []. lb = ub and the point lb is infeasible. In this case, x = lb, and fval = objconstr(x).Fval. The linear and, if present, integer constraints are infeasible together with the bounds. In this case, solve returns x = [] and fval = []. The bounds, integer, and linear constraints are feasible, but no feasible solution is found with nonlinear constraints. In this case, x is the point of least maximum infeasibility of nonlinear constraints, and fval = objconstr(x).Fval.

This table describes the exit flags for the MultiStart and GlobalSearch solvers.

Exit Flag for MultiStart or GlobalSearch	Numeric Equivalent	Meaning
LocalMinimumFoundSomeConverged	2	At least one local minimum found. Some runs of the local solver converged.
LocalMinimumFoundAllConverged	1	At least one local minimum found. All runs of the local solver converged.
SolverLimitExceeded	0	No local minimum found. Local solver called at least once and at least one local solver call ran out of iterations.
OutputFcnStop	–1	Stopped by an output function or plot function.
NoFeasibleLocalMinimumFound	–2	No feasible local minimum found.
TimeLimitExceeded	–5	MaxTime limit exceeded.
NoSolutionFound	–8	No solution found. All runs had local solver exit flag –2 or smaller, not all equal –2.
FailureInSuppliedFcn	–10	Encountered failures in the objective or nonlinear constraint functions.

This table describes the exit flags for the paretosearch solver.

Exit Flag for paretosearch	Numeric Equivalent	Meaning
SolverConvergedSuccessfully	1	One of the following conditions is met: Mesh size of all incumbents is less than options.MeshTolerance and constraints (if any) are satisfied to within options.ConstraintTolerance. Relative change in the spread of the Pareto set is less than options.ParetoSetChangeTolerance and constraints (if any) are satisfied to within options.ConstraintTolerance. Relative change in the volume of the Pareto set is less than options.ParetoSetChangeTolerance and constraints (if any) are satisfied to within options.ConstraintTolerance.
SolverLimitExceeded	0	Number of iterations exceeds options.MaxIterations, or the number of function evaluations exceeds options.MaxFunctionEvaluations.
OutputFcnStop	–1	Stopped by an output function or plot function.
NoFeasiblePointFound	–2	Solver cannot find a point satisfying all the constraints.
TimeLimitExceeded	–5	Optimization time exceeds options.MaxTime.

This table describes the exit flags for the gamultiobj solver.

Exit Flag for paretosearch	Numeric Equivalent	Meaning
SolverConvergedSuccessfully	1	Geometric average of the relative change in value of the spread over options.MaxStallGenerations generations is less than options.FunctionTolerance, and the final spread is less than the mean spread over the past options.MaxStallGenerations generations.
SolverLimitExceeded	0	Number of generations exceeds options.MaxGenerations.
OutputFcnStop	–1	Stopped by an output function or plot function.
NoFeasiblePointFound	–2	Solver cannot find a point satisfying all the constraints.
TimeLimitExceeded	–5	Optimization time exceeds options.MaxTime.

output — Information about optimization process

structure

Information about the optimization process, returned as a structure. The output structure contains the fields in the relevant underlying solver output field, depending on which solver solve called:

• 'fminbnd' output

• 'fmincon' output

• 'fminunc' output

• 'fminsearch' output

• 'fsolve' output

• 'fzero' output

• 'intlinprog' output

• 'linprog' output

• 'lsqcurvefit' or 'lsqnonlin' output

• 'lsqlin' output

• 'lsqnonneg' output

• 'quadprog' output

• 'ga' output (Global Optimization Toolbox)

• 'gamultiobj' output (Global Optimization Toolbox)

• 'paretosearch' output (Global Optimization Toolbox)

• 'particleswarm' output (Global Optimization Toolbox)

• 'patternsearch' output (Global Optimization Toolbox)

• 'simulannealbnd' output (Global Optimization Toolbox)

• 'surrogateopt' output (Global Optimization Toolbox)

• 'MultiStart' and 'GlobalSearch' return the output structure from the local solver. In addition, the output structure contains the following fields:

  • globalSolver — Either 'MultiStart' or 'GlobalSearch'.

  • objectiveDerivative — Takes the values described at the end of this section.

  • constraintDerivative — Takes the values described at the end of this section, or "auto" when prob has no nonlinear constraint.

  • solver — The local solver, such as 'fmincon'.

  • local — Structure containing extra information about the optimization.

    • sol — Local solutions, returned as a vector of OptimizationValues objects.

    • x0 — Initial points for the local solver, returned as a cell array.

    • exitflag — Exit flags of local solutions, returned as an integer vector.

    • output — Structure array, with one row for each local solution. Each row is the local output structure corresponding to one local solution.

solve includes the additional field Solver in the output structure to identify the solver used, such as 'intlinprog'.

When Solver is a nonlinear Optimization Toolbox™ solver, solve includes one or two extra fields describing the derivative estimation type. The objectivederivative and, if appropriate, constraintderivative fields can take the following values:

• "reverse-AD" for reverse automatic differentiation

• "forward-AD" for forward automatic differentiation

• "finite-differences" for finite difference estimation

• "closed-form" for linear or quadratic functions

For details, see Automatic Differentiation Background.

lambda — Lagrange multipliers at the solution

structure

Lagrange multipliers at the solution, returned as a structure.

Note

solve does not return lambda for equation-solving problems.

For the intlinprog and fminunc solvers, lambda is empty, []. For the other solvers, lambda has these fields:

• Variables – Contains fields for each problem variable. Each problem variable name is a structure with two fields:

  • Lower – Lagrange multipliers associated with the variable LowerBound property, returned as an array of the same size as the variable. Nonzero entries mean that the solution is at the lower bound. These multipliers are in the structure lambda.Variables.variablename.Lower.

  • Upper – Lagrange multipliers associated with the variable UpperBound property, returned as an array of the same size as the variable. Nonzero entries mean that the solution is at the upper bound. These multipliers are in the structure lambda.Variables.variablename.Upper.

• Constraints – Contains a field for each problem constraint. Each problem constraint is in a structure whose name is the constraint name, and whose value is a numeric array of the same size as the constraint. Nonzero entries mean that the constraint is active at the solution. These multipliers are in the structure lambda.Constraints.constraintname.

  Note

  Elements of a constraint array all have the same comparison (<=, ==, or >=) and are all of the same type (linear, quadratic, or nonlinear).

Algorithms

Conversion to Solver Form

Internally, the solve function solves optimization problems by calling a solver. For the default solver for the problem and supported solvers for the problem, see the solvers function. You can override the default by using the 'solver' name-value pair argument when calling solve.

Before solve can call a solver, the problems must be converted to solver form, either by solve or some other associated functions or objects. This conversion entails, for example, linear constraints having a matrix representation rather than an optimization variable expression.

The first step in the algorithm occurs as you place optimization expressions into the problem. An OptimizationProblem object has an internal list of the variables used in its expressions. Each variable has a linear index in the expression, and a size. Therefore, the problem variables have an implied matrix form. The prob2struct function performs the conversion from problem form to solver form. For an example, see Convert Problem to Structure.

For nonlinear optimization problems, solve uses automatic differentiation to compute the gradients of the objective function and nonlinear constraint functions. These derivatives apply when the objective and constraint functions are composed of Supported Operations for Optimization Variables and Expressions. When automatic differentiation does not apply, solvers estimate derivatives using finite differences. For details of automatic differentiation, see Automatic Differentiation Background. You can control how solve uses automatic differentiation with the ObjectiveDerivative name-value argument.

For the algorithm that intlinprog uses to solve MILP problems, see Legacy intlinprog Algorithm. For the algorithms that linprog uses to solve linear programming problems, see Linear Programming Algorithms. For the algorithms that quadprog uses to solve quadratic programming problems, see Quadratic Programming Algorithms. For linear or nonlinear least-squares solver algorithms, see Least-Squares (Model Fitting) Algorithms. For nonlinear solver algorithms, see Unconstrained Nonlinear Optimization Algorithms and Constrained Nonlinear Optimization Algorithms. For Global Optimization Toolbox solver algorithms, see Global Optimization Toolbox documentation.

For nonlinear equation solving, solve internally represents each equation as the difference between the left and right sides. Then solve attempts to minimize the sum of squares of the equation components. For the algorithms for solving nonlinear systems of equations, see Equation Solving Algorithms. When the problem also has bounds, solve calls lsqnonlin to minimize the sum of squares of equation components. See Least-Squares (Model Fitting) Algorithms.

Note

If your objective function is a sum of squares, and you want solve to recognize it as such, write it as either norm(expr)^2 or sum(expr.^2), and not as expr'*expr or any other form. The internal parser recognizes a sum of squares only when represented as a square of a norm or an explicit sums of squares. For details, see Write Objective Function for Problem-Based Least Squares. For an example, see Nonnegative Linear Least Squares, Problem-Based.

Automatic Differentiation

Automatic differentiation (AD) applies to the solve and prob2struct functions under the following conditions:

• The objective and constraint functions are supported, as described in Supported Operations for Optimization Variables and Expressions. They do not require use of the fcn2optimexpr function.

• The solver called by solve is fmincon, fminunc, fsolve, or lsqnonlin.

• For optimization problems, the 'ObjectiveDerivative' and 'ConstraintDerivative' name-value pair arguments for solve or prob2struct are set to 'auto' (default), 'auto-forward', or 'auto-reverse'.

• For equation problems, the 'EquationDerivative' option is set to 'auto' (default), 'auto-forward', or 'auto-reverse'.

When AD Applies	All Constraint Functions Supported	One or More Constraints Not Supported
Objective Function Supported	AD used for objective and constraints	AD used for objective only
Objective Function Not Supported	AD used for constraints only	AD not used

Note

For linear or quadratic objective or constraint functions, applicable solvers always use explicit function gradients. These gradients are not produced using AD. See Closed Form.

When these conditions are not satisfied, solve estimates gradients by finite differences, and prob2struct does not create gradients in its generated function files.

Solvers choose the following type of AD by default:

• For a general nonlinear objective function, fmincon defaults to reverse AD for the objective function. fmincon defaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise, fmincon defaults to forward AD for the nonlinear constraint function.

• For a general nonlinear objective function, fminunc defaults to reverse AD.

• For a least-squares objective function, fmincon and fminunc default to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.

• lsqnonlin defaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise, lsqnonlin defaults to reverse AD.

• fsolve defaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise, fsolve defaults to reverse AD.

Note

To use automatic derivatives in a problem converted by prob2struct, pass options specifying these derivatives.

options = optimoptions('fmincon','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true);
problem.options = options;

Currently, AD works only for first derivatives; it does not apply to second or higher derivatives. So, for example, if you want to use an analytic Hessian to speed your optimization, you cannot use solve directly, and must instead use the approach described in Supply Derivatives in Problem-Based Workflow.

Extended Capabilities

Automatic Parallel Support

Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

solve estimates derivatives in parallel for nonlinear solvers when the UseParallel option for the solver is true. For example,

options = optimoptions('fminunc','UseParallel',true);
[sol,fval] = solve(prob,x0,'Options',options)

solve does not use parallel derivative estimation when all objective and nonlinear constraint functions consist only of supported operations, as described in Supported Operations for Optimization Variables and Expressions. In this case, solve uses automatic differentiation for calculating derivatives. See Automatic Differentiation.

You can override automatic differentiation and use finite difference estimates in parallel by setting the 'ObjectiveDerivative' and 'ConstraintDerivative' arguments to 'finite-differences'.

When you specify a Global Optimization Toolbox solver that support parallel computation (ga (Global Optimization Toolbox), particleswarm (Global Optimization Toolbox), patternsearch (Global Optimization Toolbox), and surrogateopt (Global Optimization Toolbox)), solve compute in parallel when the UseParallel option for the solver is true. For example,

options = optimoptions("patternsearch","UseParallel",true);
[sol,fval] = solve(prob,x0,"Options",options,"Solver","patternsearch")

Version History

Introduced in R2017b

R2018b: solve(prob,solver), solve(prob,options), and solve(prob,solver,options) syntaxes have been removed

To choose options or the underlying solver for solve, use name-value pairs. For example,

sol = solve(prob,'options',opts,'solver','quadprog');

The previous syntaxes were not as flexible, standard, or extensible as name-value pairs.