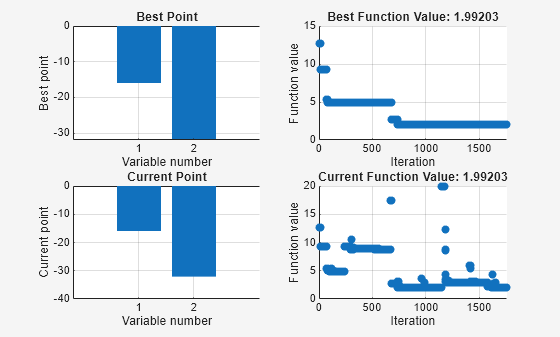
simulannealbnd
Find minimum of function using simulated annealing algorithm
Syntax
Description
x = simulannealbnd(fun,x0)x, to the function handle fun that
computes the values of the objective function. x0 is
an initial point for the simulated annealing algorithm, a real vector.
Note
Passing Extra Parameters explains how to pass extra parameters to the objective function, if necessary.
Examples
Input Arguments
Output Arguments
Alternative Functionality
App
The Optimize Live Editor task provides a visual interface for simulannealbnd.
Version History
Introduced in R2007a
See Also
ga | optimoptions | patternsearch | Optimize