Histogram2 Properties
Bivariate histogram appearance and behavior
Histogram2 properties control the appearance and behavior of the
histogram. By changing property values, you can modify aspects of the histogram. Use dot
notation to refer to a particular object and property:
h = histogram2(randn(10,1),randn(10,1)); c = h.NumBins; h.NumBins = [4 7];
Bins
Number of bins in each dimension, specified as a two-element vector of positive integers. The first element gives the number of bins in the x-dimension, and the second element gives the number of bins in the y-dimension.
If you do not specify NumBins, then histogram2 automatically calculates how many bins to use based on
the values in X and Y.
If you specify NumBins with BinMethod or
BinWidth, histogram2 only
honors the last parameter.
Example: histogram2(X,Y,'NumBins',[10
20])
Width of bins in each dimension, specified as a two-element vector of positive values. The first element gives the width of the bins in the x-dimension, and the second element gives the width of the bins in the y-dimension.
If you specify BinWidth, then histogram2 can use a maximum of 1024 bins (210) along each dimension. If instead the specified bin width requires
more bins, then histogram2 uses a larger bin width
corresponding to the maximum number of bins.
If you specify BinWidth with BinMethod or
NumBins, histogram2 only
honors the last parameter.
Example: histogram2(X,Y,'BinWidth',[5
10])5 in the
x-dimension and size 10 in the
y-dimension.
Bin edges in x-dimension, specified as a vector.
Xedges(1) is the first edge of the first bin in the
x-dimension, and Xedges(end) is the outer edge
of the last bin.
The value [X(k),Y(k)] is in the (i,j)th bin if
Xedges(i) ≤ X(k) <
Xedges(i+1)
and
Yedges(j) ≤ Y(k) <
Yedges(j+1). The last bins in each dimension also include the
last (outer) edge. For example, [X(k),Y(k)] falls into the
ith bin in the last row if Xedges(end-1) ≤
X(k) ≤ Xedges(end)
and
Yedges(i) ≤ Y(k) <
Yedges(i+1).
If you specify XBinEdges and YBinEdges with
BinMethod, BinWidth, or
NumBins, histogram2 only
honors the bin edges and the bin edges must be specified last. If you specify
XBinEdges with XBinLimits, histogram2 only honors the XBinEdges and the
XBinEdges must be specified last.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Bin edges in y-dimension, specified as a vector.
Yedges(1) is the first edge of the first bin in the
y-dimension, and Yedges(end) is the outer edge
of the last bin.
The value [X(k),Y(k)] is in the (i,j)th bin if
Xedges(i) ≤ X(k) <
Xedges(i+1)
and
Yedges(j) ≤ Y(k) <
Yedges(j+1). The last bins in each dimension also include the last
(outer) edge. For example, [X(k),Y(k)] falls into the
ith bin in the last row if Xedges(end-1) ≤
X(k) ≤ Xedges(end)
and
Yedges(i) ≤ Y(k) <
Yedges(i+1).
If you specify XBinEdges and YBinEdges with
BinMethod, BinWidth, or
NumBins, histogram2 only honors
the bin edges and the bin edges must be specified last. If you specify
YBinEdges with YBinLimits, histogram2 only honors the YBinEdges and the
YBinEdges must be specified last.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Bin limits in x-dimension, specified as a two-element vector,
[xbmin,xbmax]. The first element indicates the first bin edge in
the x-dimension. The second element indicates the last bin edge in
the x-dimension.
This option only bins data that falls within the bin limits inclusively,
X>=xbmin & X<=xbmax.
Selection mode for bin limits in x-dimension, specified as
'auto' or 'manual'. The default value is
'auto', so that the bin limits automatically adjust to the data
along the x-axis.
If you explicitly specify either XBinLimits or
XBinEdges, then XBinLimitsMode is set
automatically to 'manual'. In that case, specify
XBinLimitsMode as 'auto' to rescale the bin
limits to the data.
Bin limits in y-dimension, specified as a two-element vector,
[ybmin,ybmax]. The first element indicates the first bin edge in
the y-dimension. The second element indicates the last bin edge in
the y-dimension.
This option only bins data that falls within the bin limits inclusively,
Y>=ybmin & Y<=ybmax.
Selection mode for bin limits in y-dimension, specified as
'auto' or 'manual'. The default value is
'auto', so that the bin limits automatically adjust to the data
along the y-axis.
If you explicitly specify either YBinLimits or
YBinEdges, then YBinLimitsMode is set
automatically to 'manual'. In that case, specify
YBinLimitsMode as 'auto' to rescale the bin
limits to the data.
Binning algorithm, specified as one of the values in this table.
| Value | Description |
|---|---|
'auto' | The default |
'scott' | Scott’s rule is optimal if the data is close to being jointly
normally distributed. This rule is appropriate for most other
distributions, as well. It uses a bin size of
|
'fd' | The Freedman-Diaconis rule is less sensitive to outliers in the
data, and might be more suitable for data with heavy-tailed
distributions. It uses a bin size of
|
'integers' | The integer rule is useful with integer data, as it creates bins centered on pairs of integers. It uses a bin width of 1 for each dimension and places bin edges halfway between integers. To avoid accidentally creating too many bins, you can use this rule to create a limit of 1024 bins (210). If the data range for either dimension is greater than 1024, then the integer rule uses wider bins instead. |
histogram2adjusts the number of bins slightly so that the bin edges fall on "nice" numbers, rather than using these exact formulas.If you set the
NumBins,XBinEdges,YBinEdges,BinWidth,XBinLimits, orYBinLimitsproperties, thenBinMethodis set to'manual'.If you specify
BinMethodwithBinWidthorNumBins,histogram2only honors the last parameter.
Example: histogram2(X,Y,'BinMethod','integers')
Toggle display of empty bins, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0 (false). A value
of 'on' is equivalent to true, and
'off' is equivalent to false. Thus, you can use
the value of this property as a logical value. The value is stored as an on/off logical
value of type matlab.lang.OnOffSwitchState.
Example: histogram2(X,Y,'ShowEmptyBins','on') turns on the display
of empty bins.
Data
Data to distribute among bins, specified as a matrix of size
m-by-2. The X and
Y inputs to histogram2 correspond to the
columns in Data, that is, Data(:,1) is
X(:) and Data(:,2) is
Y(:).
histogram2 ignores all NaN values.
Similarly,histogram2 ignores Inf and
-Inf values, unless the bin edges explicitly specify
Inf or -Inf as a bin edge. Although
NaN, Inf, and -Inf values are
typically not plotted, they are still included in normalization calculations that
include the total number of data elements, such as
'probability'.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
This property is read-only.
Bin values, returned as a numeric matrix. If Normalization is
'count', then the (i,j)th entry in
Values specifies the bin count for the bin whose
x edges are [Xedges(i), Xedges(i+1)] and whose
y edges are [Yedges(j), Yedges(j+1)].
Depending on the value of Normalization, the
Values property instead can contain a normalized variant of the bin
counts.
The binning scheme includes the leading x-dimension and y-dimension edge of each bin as well as the trailing edge for the last bins along the x-dimension and y-dimension.
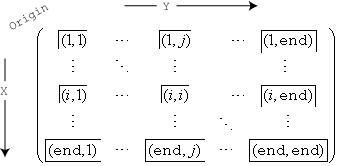
For example, the (1,1) bin includes values that fall on the first
edge in each dimension, and the last bin in the bottom right includes values that fall
on any of its edges.
Type of normalization, specified as one of the values in this table. For each
bin i:
is the bin value.
is the number of elements in the bin.
is the area of the bin, computed using the x and y bin widths.
is the number of elements in the input data. This value can be greater than the binned data if the data contains missing values or if some of the data lies outside the bin limits.
| Value | Bin Values | Notes |
|---|---|---|
'count' (default) |
|
|
'probability' |
|
|
'percentage' |
|
|
'countdensity' |
|
|
'cumcount' |
|
|
'pdf' |
|
|
'cdf' |
|
|
Example: histogram2(X,Y,'Normalization','pdf')
Bin counts, specified as a matrix. Use this input to pass bin counts to
histogram2 when the bin counts calculation is performed
separately and you do not want histogram2 to do any data binning.
countsmust be a matrix of size[nbinsX nbinsY]so that it specifies a bin count for each bin.The number of bins in the x-dimension is
length(XBinEdges)-1, and the number of bins in the y-dimension islength(YBinEdges)-1.Compared to the
Valuesproperty,BinCountsis not normalized. IfNormalizationis'count', thenValuesandBinCountsare equivalent.
Example: histogram2('XBinEdges',-1:1,'YBinEdges',-2:2,'BinCounts',[1 2 3 4;
5 6 7 8])
Selection mode for bin counts, specified as 'auto' or
'manual'. The default value is 'auto', so that
the bin counts are automatically computed from Data,
XBinEdges, and YBinEdges.
If you specify BinCounts, then BinCountsMode
is automatically set to 'manual'. Similarly, if you specify
Data, then BinCountsMode is automatically set to
'auto'.
Color and Styling
Histogram display style, specified as either 'bar3' or
'tile'.
'bar3'— Display the histogram using 3-D bars.'tile'— Display the histogram as a rectangular array of tiles with colors indicating the bin values.
Example: histogram2(X,Y,'DisplayStyle','tile') plots the histogram
as a rectangular array of tiles.
Histogram bar color, specified as one of these values:
'none'— Bars are not filled.'flat'— Bar colors vary with height. Bars with different heights have different colors. The colors are selected from the figure or axes colormap.'auto'— Histogram bar color is chosen automatically (default).RGB triplet, hexadecimal color code, or color name — Bars are filled with the specified color.
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
Color Name Short Name RGB Triplet Hexadecimal Color Code Appearance "red""r"[1 0 0]"#FF0000"
"green""g"[0 1 0]"#00FF00"
"blue""b"[0 0 1]"#0000FF"
"cyan""c"[0 1 1]"#00FFFF"
"magenta""m"[1 0 1]"#FF00FF"
"yellow""y"[1 1 0]"#FFFF00"
"black""k"[0 0 0]"#000000"
"white""w"[1 1 1]"#FFFFFF"
This table lists the default color palettes for plots in the light and dark themes.
Palette Palette Colors "gem"— Light theme defaultBefore R2025a: Most plots use these colors by default.

"glow"— Dark theme default
You can get the RGB triplets and hexadecimal color codes for these palettes using the
orderedcolorsandrgb2hexfunctions. For example, get the RGB triplets for the"gem"palette and convert them to hexadecimal color codes.RGB = orderedcolors("gem"); H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using
RGB = get(groot,"FactoryAxesColorOrder").Before R2024a: Get the hexadecimal color codes using
H = compose("#%02X%02X%02X",round(RGB*255)).
If you specify DisplayStyle as 'tile', then the
FaceColor property is set to 'flat'.
Example: histogram2(X,Y,'FaceColor','g')
Histogram edge color, specified as one of these values:
'none'— Edges are not drawn.'auto'— Color of each edge is chosen automatically.RGB triplet, hexadecimal color code, or color name — Edges use the specified color.
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
Color Name Short Name RGB Triplet Hexadecimal Color Code Appearance "red""r"[1 0 0]"#FF0000"
"green""g"[0 1 0]"#00FF00"
"blue""b"[0 0 1]"#0000FF"
"cyan""c"[0 1 1]"#00FFFF"
"magenta""m"[1 0 1]"#FF00FF"
"yellow""y"[1 1 0]"#FFFF00"
"black""k"[0 0 0]"#000000"
"white""w"[1 1 1]"#FFFFFF"
This table lists the default color palettes for plots in the light and dark themes.
Palette Palette Colors "gem"— Light theme defaultBefore R2025a: Most plots use these colors by default.

"glow"— Dark theme default
You can get the RGB triplets and hexadecimal color codes for these palettes using the
orderedcolorsandrgb2hexfunctions. For example, get the RGB triplets for the"gem"palette and convert them to hexadecimal color codes.RGB = orderedcolors("gem"); H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using
RGB = get(groot,"FactoryAxesColorOrder").Before R2024a: Get the hexadecimal color codes using
H = compose("#%02X%02X%02X",round(RGB*255)).
Example: histogram2(X,Y,'EdgeColor','r')
Transparency of histogram bars, specified as a scalar value in range
[0,1]. histogram2 uses the
same transparency for all the bars of the histogram. A value of 1
means fully opaque and 0 means completely transparent
(invisible).
Example: histogram2(X,Y,'FaceAlpha',0.5) creates a bivariate
histogram plot with semi-transparent bars.
Transparency of histogram bar edges, specified as a scalar value in the range
[0,1]. A value of 1 means fully opaque and
0 means completely transparent (invisible).
Example: histogram2(X,Y,'EdgeAlpha',0.5) creates a bivariate
histogram plot with semi-transparent bar edges.
Lighting effect on histogram bars, specified as one of these values.
| Value | Description |
|---|---|
'lit' |
Histogram bars display a pseudo-lighting effect, where the sides of the bars use darker colors relative to the tops. The bars are unaffected by other light sources in the axes. This is the default value when |
'flat' |
Histogram bars are not lit automatically. In the presence of other light objects, the lighting effect is uniform across the bar faces. |
'none' |
Histogram bars are not lit automatically, and lights do not affect the histogram bars.
|
Example: histogram2(X,Y,'FaceLighting','none') turns off the
lighting of the histogram bars.
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
Width of bar outlines, specified as a positive value in point units. One point equals 1/72 inch.
Example: 1.5
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Series index, specified as a positive integer or "none". This property is
useful for reassigning the face colors of Histogram2 objects so that
they match the colors of other objects.
By default, the SeriesIndex property of a Histogram2
object is a number that corresponds to its order of creation, starting at
1. MATLAB® uses the number to calculate indices for assigning colors when you call
plotting functions. The indices refer to the rows of the arrays stored in the
ColorOrder property of the axes. Any objects in the axes that
have the same SeriesIndex number will have the same color.
A SeriesIndex value of "none" corresponds to a
neutral color that does not participate in the indexing scheme.
How Manual Color Assignment Overrides SeriesIndex Behavior
To manually control face color, set the FaceColor property of
the Histogram2 object to a color value, such as a color name or
an RGB triplet.
When you manually set the face color of a Histogram2 object,
MATLAB disables automatic color selection for that object and allows your
color to persist, regardless of the value of the SeriesIndex
property.
To enable automatic selection again, set the SeriesIndex
property to positive integer, and set the FaceColor property to
"auto".
In some cases, MATLAB sets the SeriesIndex value to
0, which also disables automatic color selection.
Legend
Text used by the legend, specified as a character vector. The text appears next to an icon of the histogram2.
Example: 'Text Description'
For multiline text, create the character vector using sprintf
with the new line character \n.
Example: sprintf('line one\nline two')
Alternatively, you can specify the legend text using the legend function.
If you specify the text as an input argument to the
legendfunction, then the legend uses the specified text and sets theDisplayNameproperty to the same value.If you do not specify the text as an input argument to the
legendfunction, then the legend uses the text in theDisplayNameproperty. By default,DisplayNameis a character vector representing the variable names of the x and y input data used to construct the histogram. If one or both of the inputs do not have variable names, thenDisplayNameis empty,''.
If the DisplayName property does not contain any text, then the
legend generates a character vector. The character vector has the form
'dataN', where N is the number assigned to the
histogram2 object based on its location in the list of legend
entries.
If you edit interactively the character vector in an existing legend, then
MATLAB updates the DisplayName property to the edited
character vector.
Include the object in the legend, specified as an Annotation
object. Set the underlying IconDisplayStyle property of the
Annotation object to one of these values:
"on"— Include the object in the legend (default)."off"— Do not include the object in the legend.
For example, to exclude the Histogram2 object named
obj from the legend, set the IconDisplayStyle
property to "off".
obj.Annotation.LegendInformation.IconDisplayStyle = "off";
Alternatively, you can control the items in a legend using the legend function. Specify the first input argument as a vector of the
graphics objects to include. If you do not specify an existing graphics object in the
first input argument, then it does not appear in the legend. However, graphics objects
added to the axes after the legend is created do appear in the legend. Consider creating
the legend after creating all the plots to avoid extra items.
Interactivity
State of visibility, specified as "on" or "off", or as
numeric or logical 1 (true) or
0 (false). A value of "on"
is equivalent to true, and "off" is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
"on"— Display the object."off"— Hide the object without deleting it. You still can access the properties of an invisible object.
Data tip content, specified as a DataTipTemplate object. You can
control the content that appears in a data tip by modifying the properties of the
underlying DataTipTemplate object. For a list of properties, see
DataTipTemplate Properties.
For an example of modifying data tips, see Create Custom Data Tips.
Note
The DataTipTemplate object is not returned by
findobj or findall, and it is not
copied by copyobj.
Context menu, specified as a ContextMenu object. Use this property
to display a context menu when you right-click the object. Create the context menu using
the uicontextmenu function.
Note
If the PickableParts property is set to
'none' or if the HitTest property is set
to 'off', then the context menu does not appear.
Selection state, specified as 'on' or 'off', or as
numeric or logical 1 (true) or
0 (false). A value of 'on'
is equivalent to true, and 'off' is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
'on'— Selected. If you click the object when in plot edit mode, then MATLAB sets itsSelectedproperty to'on'. If theSelectionHighlightproperty also is set to'on', then MATLAB displays selection handles around the object.'off'— Not selected.
Display of selection handles when selected, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0 (false). A
value of 'on' is equivalent to true, and
'off' is equivalent to false. Thus, you can
use the value of this property as a logical value. The value is stored as an on/off
logical value of type matlab.lang.OnOffSwitchState.
'on'— Display selection handles when theSelectedproperty is set to'on'.'off'— Never display selection handles, even when theSelectedproperty is set to'on'.
Callbacks
Mouse-click callback, specified as one of these values:
Function handle
Cell array containing a function handle and additional arguments
Character vector that is a valid MATLAB command or function, which is evaluated in the base workspace (not recommended)
Use this property to execute code when you click the object. If you specify this property using a function handle, then MATLAB passes two arguments to the callback function when executing the callback:
Clicked object — Access properties of the clicked object from within the callback function.
Event data — Empty argument. Replace it with the tilde character (
~) in the function definition to indicate that this argument is not used.
For more information on how to use function handles to define callback functions, see Create Callbacks for Graphics Objects.
Note
If the PickableParts property is set to 'none' or
if the HitTest property is set to 'off',
then this callback does not execute.
Object creation function, specified as one of these values:
Function handle.
Cell array in which the first element is a function handle. Subsequent elements in the cell array are the arguments to pass to the callback function.
Character vector containing a valid MATLAB expression (not recommended). MATLAB evaluates this expression in the base workspace.
For more information about specifying a callback as a function handle, cell array, or character vector, see Create Callbacks for Graphics Objects.
This property specifies a callback function to execute when MATLAB creates the object. MATLAB initializes all property values before executing the CreateFcn callback. If you do not specify the CreateFcn property, then MATLAB executes a default creation function.
Setting the CreateFcn property on an existing component has no effect.
If you specify this property as a function handle or cell array, you can access the object that is being created using the first argument of the callback function. Otherwise, use the gcbo function to access the object.
Object deletion function, specified as one of these values:
Function handle.
Cell array in which the first element is a function handle. Subsequent elements in the cell array are the arguments to pass to the callback function.
Character vector containing a valid MATLAB expression (not recommended). MATLAB evaluates this expression in the base workspace.
For more information about specifying a callback as a function handle, cell array, or character vector, see Create Callbacks for Graphics Objects.
This property specifies a callback function to execute when MATLAB deletes the object. MATLAB executes the DeleteFcn callback before destroying the
properties of the object. If you do not specify the DeleteFcn
property, then MATLAB executes a default deletion function.
If you specify this property as a function handle or cell array, you can access the object that is being deleted using the first argument of the callback function. Otherwise, use the gcbo function to access the object.
Callback Execution Control
Callback interruption, specified as 'on' or 'off', or as
numeric or logical 1 (true) or
0 (false). A value of 'on'
is equivalent to true, and 'off' is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
This property determines if a running callback can be interrupted. There are two callback states to consider:
The running callback is the currently executing callback.
The interrupting callback is a callback that tries to interrupt the running callback.
MATLAB determines callback interruption behavior whenever it executes a command that
processes the callback queue. These commands include drawnow, figure, uifigure, getframe, waitfor, and pause.
If the running callback does not contain one of these commands, then no interruption occurs. MATLAB first finishes executing the running callback, and later executes the interrupting callback.
If the running callback does contain one of these commands, then the
Interruptible property of the object that owns the running
callback determines if the interruption occurs:
If the value of
Interruptibleis'off', then no interruption occurs. Instead, theBusyActionproperty of the object that owns the interrupting callback determines if the interrupting callback is discarded or added to the callback queue.If the value of
Interruptibleis'on', then the interruption occurs. The next time MATLAB processes the callback queue, it stops the execution of the running callback and executes the interrupting callback. After the interrupting callback completes, MATLAB then resumes executing the running callback.
Note
Callback interruption and execution behave differently in these situations:
If the interrupting callback is a
DeleteFcn,CloseRequestFcn, orSizeChangedFcncallback, then the interruption occurs regardless of theInterruptibleproperty value.If the running callback is currently executing the
waitforfunction, then the interruption occurs regardless of theInterruptibleproperty value.If the interrupting callback is owned by a
Timerobject, then the callback executes according to schedule regardless of theInterruptibleproperty value.
Callback queuing, specified as 'queue' or 'cancel'. The BusyAction property determines how MATLAB handles the execution of interrupting callbacks. There are two callback states to consider:
The running callback is the currently executing callback.
The interrupting callback is a callback that tries to interrupt the running callback.
The BusyAction property determines callback queuing behavior only
when both of these conditions are met:
Under these conditions, the BusyAction property of the
object that owns the interrupting callback determines how MATLAB handles the interrupting callback. These are possible values of the
BusyAction property:
'queue'— Puts the interrupting callback in a queue to be processed after the running callback finishes execution.'cancel'— Does not execute the interrupting callback.
Ability to capture mouse clicks, specified as one of these values:
'visible'— Capture mouse clicks only when visible. TheVisibleproperty must be set to'on'. TheHitTestproperty determines if theHistogram2object responds to the click or if an ancestor does.'none'— Cannot capture mouse clicks. Clicking theHistogram2object passes the click to the object behind it in the current view of the figure window. TheHitTestproperty of theHistogram2object has no effect.
Response to captured mouse clicks, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0 (false). A
value of 'on' is equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this property as
a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
'on'— Trigger theButtonDownFcncallback of theHistogram2object. If you have defined theContextMenuproperty, then invoke the context menu.'off'— Trigger the callbacks for the nearest ancestor of theHistogram2object that meets one of these conditions:HitTestproperty is set to'on'.PickablePartsproperty is set to a value that enables the ancestor to capture mouse clicks.
Note
The PickableParts property determines if
the Histogram2 object can capture
mouse clicks. If it cannot, then the HitTest property
has no effect.
This property is read-only.
Deletion status, returned as an on/off logical value of type matlab.lang.OnOffSwitchState.
MATLAB sets the BeingDeleted property to
'on' when the DeleteFcn callback begins
execution. The BeingDeleted property remains set to
'on' until the component object no longer exists.
Check the value of the BeingDeleted property to verify that the object is not about to be deleted before querying or modifying it.
Parent/Child
Parent, specified as an Axes, Group,
or Transform object.
Children, returned as an empty GraphicsPlaceholder array or a
DataTip object array. Use this property to view a list of data tips
that are plotted on the chart.
You cannot add or remove children using the Children property. To add a
child to this list, set the Parent property of the
DataTip object to the chart object.
Visibility of the object handle in the Children property
of the parent, specified as one of these values:
"on"— Object handle is always visible."off"— Object handle is invisible at all times. This option is useful for preventing unintended changes by another function. SetHandleVisibilityto"off"to temporarily hide the handle during the execution of that function."callback"— Object handle is visible from within callbacks or functions invoked by callbacks, but not from within functions invoked from the command line. This option blocks access to the object at the command line, but permits callback functions to access it.
If the object is not listed in the Children property of the parent, then
functions that obtain object handles by searching the object hierarchy or querying
handle properties cannot return it. Examples of such functions include the
get, findobj, gca, gcf, gco, newplot, cla, clf, and close functions.
Hidden object handles are still valid. Set the root ShowHiddenHandles
property to "on" to list all object handles regardless of their
HandleVisibility property setting.
Identifiers
This property is read-only.
Type of graphics object, returned as 'histogram2'. Use this
property to find all objects of a given type within a plotting hierarchy, such as
searching for the type using findobj.
Object identifier, specified as a character vector or string scalar. You can specify a unique Tag value to serve as an identifier for an object. When you need access to the object elsewhere in your code, you can use the findobj function to search for the object based on the Tag value.
User data, specified as any MATLAB array. For example, you can specify a scalar, vector, matrix, cell array, character array, table, or structure. Use this property to store arbitrary data on an object.
If you are working in App Designer, create public or private properties in the app to share data instead of using the UserData property. For more information, see Share Data Within App Designer Apps.
Version History
Introduced in R2015bYou can create histograms with percentages on the vertical axis by setting the
Normalization property to 'percentage'.
Opt out of automatic color selection for Histogram2 objects by setting the
SeriesIndex property to "none". When you specify
"none", the Histogram2 object has a neutral
color.
To enable automatic color selection again, set the SeriesIndex property to a positive whole number.
Control how Histogram2 objects vary in color by setting the
SeriesIndex property. This property is useful when you want to
match the colors of different objects in the axes.
Starting in R2020a, using the UIContextMenu property to assign a
context menu to a graphics object or UI component is not recommended. Use the
ContextMenu property instead. The property values are the
same.
There are no plans to remove support for the UIContextMenu property
at this time. However, the UIContextMenu property no longer appears in
the list returned by calling the get function on a graphics object or UI
component.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)