islocalmax2

Find local maxima in 2-D data

Since R2024a

Syntax

TF = islocalmax2(A)

[TF,P] = islocalmax2(A)

___ = islocalmax2(A,Name=Value)

Description

TF = islocalmax2(A) returns a logical array whose elements are 1 (true) when a local maximum is detected in the corresponding element of A.

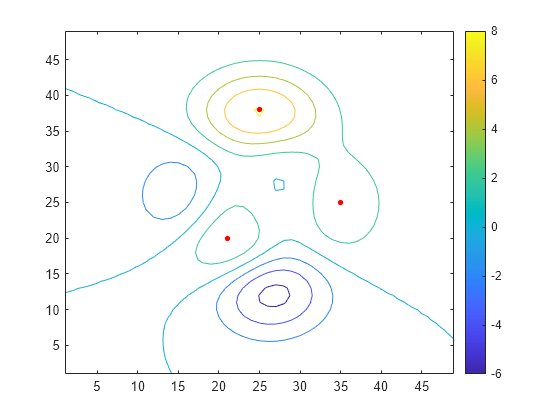
[TF,P] = islocalmax2(A) also returns the prominence corresponding to each element of A. For more information about the prominence calculation, see Algorithms.

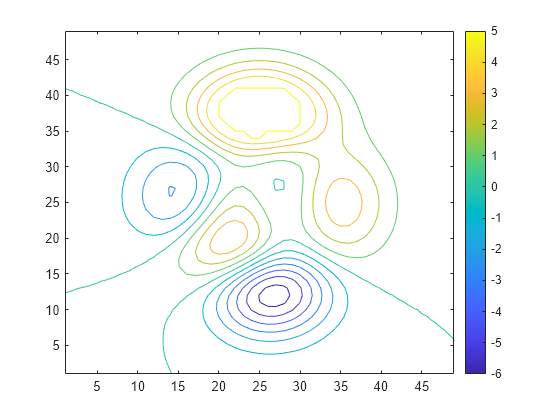
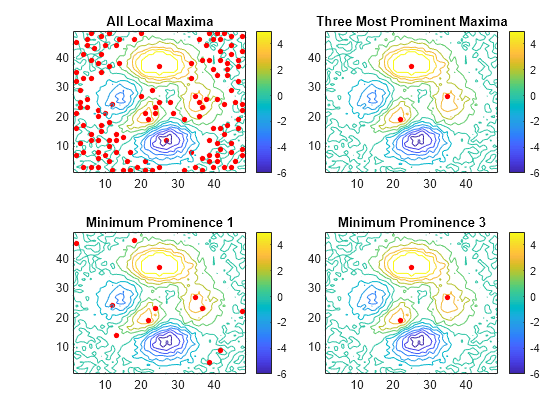
___ = islocalmax2(A,Name=Value) specifies options for finding local maxima using one or more name-value arguments with either of the output argument combinations in the previous syntaxes. For example, TF = islocalmax2(A,MaxNumExtrema=4) finds no more than four of the most prominent local maxima.

Examples

Find Locations and Values of Local Maxima

Create a matrix, and visualize the matrix using a contour plot.

A = peaks;
contour(A)
colorbar

Determine the locations of the local maxima.

TF = islocalmax2(A);

Use the local maxima indicator to determine the value of each maximum.

maxval = A(TF)

maxval = 3×1

    3.7573
    8.0752
    3.5823

Plot the local maxima on the contour plot.

[X,Y] = meshgrid(1:49,1:49);
hold on
plot3(X(TF),Y(TF),maxval,"red.",MarkerSize=12)

Customize Maxima Selection from Flat Region

Create and visualize a matrix with a flat region.

data = peaks;
A = clip(data,-Inf,5);
contour(A)
colorbar

Find the local maxima. By default, TF is 1 (true) for only the center point of the flat region and TF is 0 (false) for all other points on the flat region.

[TF P] = islocalmax2(A);

To select only the point on the flat region with the smallest linear index as the local maximum, specify the FlatSelection name-value argument as "first".

[TF2 P2] = islocalmax2(A,FlatSelection="first");

To select all points on the flat region as local maxima, specify FlatSelection as "all".

[TF3 P3] = islocalmax2(A,FlatSelection="all");

Compare the results of the flat region selections by visualizing the extrema.

[X,Y] = meshgrid(1:49,1:49);
tiledlayout(2,2)

nexttile
contour(A)
colorbar
hold on
plot3(X(TF),Y(TF),A(TF),"r.",MarkerSize=12)
title("Center Point on Flat Region")

nexttile
contour(A)
colorbar
hold on
plot3(X(TF2),Y(TF2),A(TF2),"r.",MarkerSize=12)
title("First Point on Flat Region")

nexttile
contour(A)
colorbar
hold on
plot3(X(TF3),Y(TF3),A(TF3),"r.",MarkerSize=12)
title("All Points on Flat Region")

Only the local maxima indicator changes when you specify FlatSelection. The prominence of all data points is the same for all values of FlatSelection.

isequal(P,P2,P3)

ans = logical
   1

Filter Noise

Create a matrix with some noise, and visualize the matrix using a contour plot.

data = peaks;
data = data + randn(49)*0.3;
A = clip(data,-Inf,5);

contour(A)
colorbar

Find the local maxima and plot them on the surface plot. By default, islocalmax2 finds all local maxima whose prominence is greater than 0.

[TF P] = islocalmax2(A);

To understand the prominence of the local maxima, sort the unique prominence values.

maxP = sort(unique(P(:)),"descend")

maxP = 143×1

    5.7516
    3.9830
    3.3811
    2.6829
    1.7200
    1.2871
    1.2853
    1.1382
    1.1128
    1.0921
      ⋮

Ignore the local maxima that are a result of noise by finding only the three most prominent local maxima. When you specify the MaxNumExtrema name-value argument, the points in a flat region are jointly considered a single maximum point.

TF2 = islocalmax2(A,MaxNumExtrema=3);

Find local maxima whose prominence is greater than 1.

TF3 = islocalmax2(A,MinProminence=1);

Find local maxima whose prominence is greater than 3.

TF4 = islocalmax2(A,MinProminence=3);

Compare the results of the prominence filters by visualizing the extrema.

[X,Y] = meshgrid(1:49,1:49);
figure
tiledlayout(2,2)

nexttile
contour(A)
colorbar
hold on
plot3(X(TF),Y(TF),A(TF),"r.",MarkerSize=12)
title("All Local Maxima")

nexttile
contour(A)
colorbar
hold on
plot3(X(TF2),Y(TF2),A(TF2),"r.",MarkerSize=12)
title("Three Most Prominent Maxima")

nexttile
contour(A)
colorbar
hold on
plot3(X(TF3),Y(TF3),A(TF3),"r.",MarkerSize=12)
title("Minimum Prominence 1")

nexttile
contour(A)
colorbar
hold on
plot3(X(TF4),Y(TF4),A(TF4),"r.",MarkerSize=12)
title("Minimum Prominence 3")

Alternatively, you can use the smoothdata2 function to remove noise prior to finding the local maxima.

Compute Prominence Across Specified Window

Create a matrix of data with one isolated peak and many peaks with high density elsewhere in the data.

rng("default")
data = zeros(100);
data(30,30) = 1000;
data = smoothdata2(data,"gaussian",50);
smallPeakLoc = randi(10000,1,400);
tempData = zeros(100)+1;
tempData(smallPeakLoc) = abs(randn(1,400))*3;
tempData(1:50,1:50) = 0;
A = data+tempData;
A = smoothdata2(A,"gaussian",5);

contour(A)
colorbar

Because of the high density of peaks elsewhere in the data, islocalmax2 underestimates the prominence of the peak at (30,30).

TF = islocalmax2(A,MaxNumExtrema=10);
[X,Y] = meshgrid(1:100,1:100);

contour(A)
colorbar
hold on
plot3(X(TF),Y(TF),A(TF),"r.",MarkerSize=20)

To limit the impact of distant peaks on the prominence calculation, specify a prominence window. The isolated peak at (30,30) is now marked as a local maxima.

TF2 = islocalmax2(A,ProminenceWindow=50,MaxNumExtrema=10);
contour(A)
colorbar
hold on
plot3(X(TF2),Y(TF2),A(TF2),"r.",MarkerSize=20)

Input Arguments

A — Input data

vector | matrix | multidimensional array

Input data, specified as a vector, matrix, or multidimensional array.

islocalmax2 ignores missing values when computing the local maxima.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: TF = islocalmax2(A,MinProminence=2)

SamplePoints — Sample points

two-element cell array

Sample points, specified as a two-element cell array of vectors of sample point values. The sample points in the first vector represent the data locations along the columns of A, and the sample points in the second vector represent the data locations along the rows of A.

Both vectors must be sorted and must not contain duplicate elements. Sample points do not need to be uniformly spaced. If A is an m-by-n matrix, then the default value of SamplePoints is {1:n 1:m}.

The prominence window is defined relative to the sample points. When the sample point vectors have data type datetime or duration, the prominence window size must have type duration.

Example: islocalmax2(A,SamplePoints={1:5,10:2:18})

MinProminence — Minimum prominence

0 (default) | nonnegative scalar

Minimum prominence, specified as a nonnegative scalar. islocalmax2 returns only local maxima whose prominence is at least the specified value.

ProminenceWindow — Prominence window size

positive integer or duration scalar | two-element cell array of positive integer or duration values | two-element cell array of two-element vectors of nonnegative integer or duration values

Prominence window size, specified as a positive integer or duration scalar, two-element cell array of positive integer or duration values, or two-element cell array of two-element vectors of nonnegative integer or duration values. islocalmax2 defines the window relative to the sample points.

• If ProminenceWindow is a positive integer scalar k, then the window is a k-by-k block centered about the current element.

• If ProminenceWindow is a two-element cell array of positive integers {m n}, then the window is an m-by-n block centered about the current element.

• If ProminenceWindow is a two-element cell array of two-element vectors of nonnegative integers {[bRow fRow] [bCol fCol]}, then the window contains the row and column of the current element, the preceding bRow and succeeding fRow rows, and the preceding bCol and succeeding fCol columns.

If you specify SamplePoints using datetime or duration values, then ProminenceWindow must be of type duration.

Example: islocalmax2(A,ProminenceWindow=4)

Example: islocalmax2(A,ProminenceWindow={2 3})

Example: islocalmax2(A,ProminenceWindow={[0 2] [3 3]})

FlatSelection — Flat region indicator

"center" (default) | "first" | "all"

Flat region indicator for when a local maximum value is repeated in adjacent elements, specified as one of these values:

• "center" — Select only the center (centroid) element of a flat region as the local maximum. "center" indicates exactly one local maximum per flat section.

• "first" — Select only the first element of a flat region as the local maximum, where the first element is the element with the smallest linear index. "first" indicates exactly one local maximum per flat section and guarantees that all elements of TF with a value of 1 (true) are extrema.

• "all" — Select all the elements of a flat region as the local maxima. The number of elements of TF with a value of 1 (true) does not match the number of local maxima.

When you specify the MinSeparation or MaxNumExtrema name-value argument, flat region points are jointly considered a single maximum point.

MinSeparation — Minimum separation

0 (default) | nonnegative integer or duration scalar | two-element cell array of positive integer or duration values

Minimum separation between local maxima, specified as 0, a nonnegative integer or duration scalar, or a two-element cell array of positive integer or duration values.

If MinSeparation is a scalar, it is the Euclidean distance between maxima. If MinSeparation is a cell array, the first element specifies the minimum distance between maxima along the columns of A and the second element specifies the minimum distance along the rows of A. The separation values are defined in the same units as the sample points vectors, which are [1 2 3 ...] by default.

When the separation value is greater than 0, islocalmax2 selects the most prominent local maximum and ignores all other local maxima within the specified separation. This process is repeated until there are no more local maxima detected.

If you specify SamplePoints using datetime or duration values, the corresponding element in MinSeparation must be of type duration.

Example: islocalmax2(A,MinSeparation=3)

Example: islocalmax2(A,SamplePoints={1:10,hours(1:10)},MinSeparation={3,hours(4)})

MaxNumExtrema — Maximum number of maxima

Inf (default) | positive integer scalar

Maximum number of maxima to detect, specified as a positive integer scalar. islocalmax2 finds no more than the specified number of the most prominent maxima.

Output Arguments

TF — Local maxima indicator

vector | matrix | multidimensional array

Local maxima indicator, returned as a vector, matrix, or multidimensional array. TF is the same size as A.

Data Types: logical

P — Prominence

vector | matrix | multidimensional array

Prominence, returned as a vector, matrix, or multidimensional array. The prominence of a local maximum (or peak) measures how the peak stands out with respect to its height and location relative to other peaks. For more information about the prominence calculation, see Algorithms.

P is the same size as A. If the input data has a signed or unsigned integer type, then P contains unsigned integers.

Algorithms

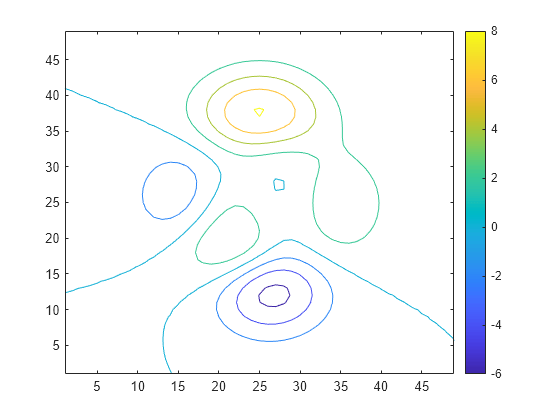
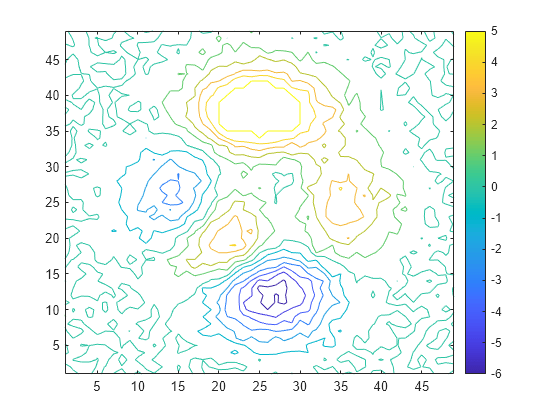
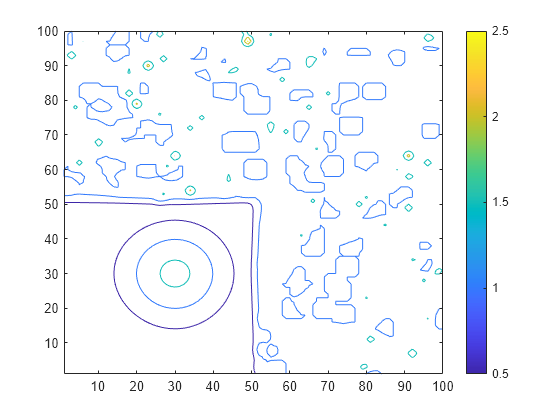
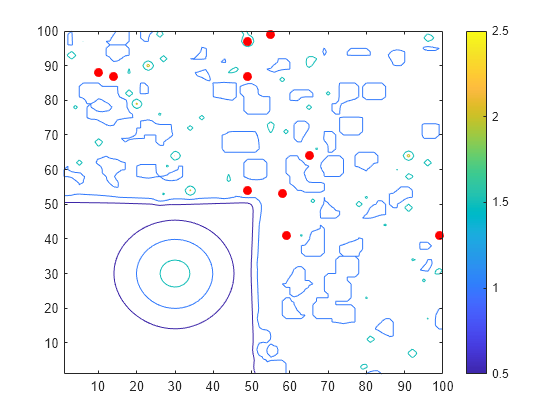
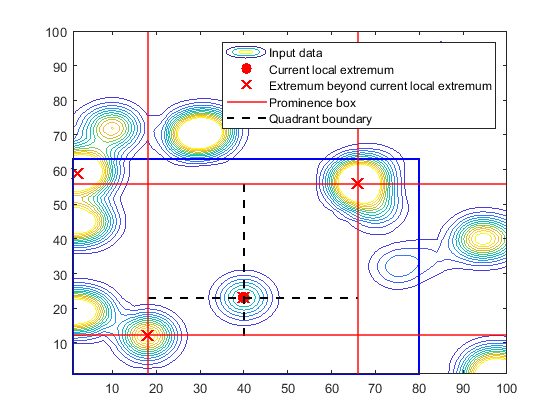
islocalmax2 identifies all local maxima in the input data and follows these steps to compute the prominence of each local maximum:

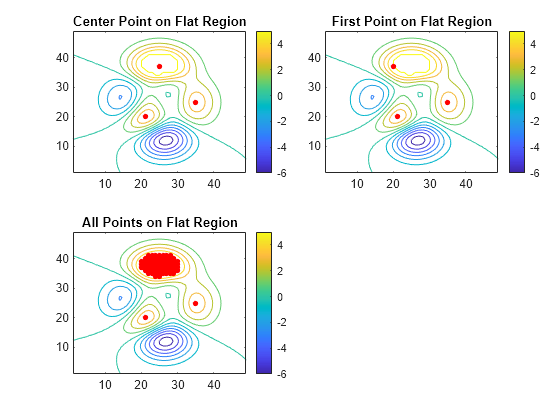
1. Determine the data to use to compute the prominence.

   • If the ProminenceWindow name-value argument is specified, use its value to draw a rectangular window of data around the current local maximum. Otherwise, use a rectangular window that includes all of the data.

2. Determine the prominence box.

   • Move vertical lines left and right from the current maximum until encountering a higher maximum or the edge of the rectangular window.

   • Move horizontal lines up and down from the current maximum until encountering a higher maximum or the edge of the rectangular window.

3. Compute the prominence.

   • Divide the prominence box into four quadrants centered on the current local maximum.

   • Identify the lowest value within each quadrant.

   • Use the highest of these quadrant minimum values as the basis value. The prominence is the absolute difference between the height of the current local maximum and the basis value.

Version History

Introduced in R2024a