islocalmax

Find local maxima

Syntax

TF = islocalmax(A)

TF = islocalmax(A,dim)

TF = islocalmax(___,Name,Value)

[TF,P] = islocalmax(___)

Description

TF = islocalmax(A) returns a logical array whose elements are 1 (true) when a local maximum is detected in the corresponding element of A.

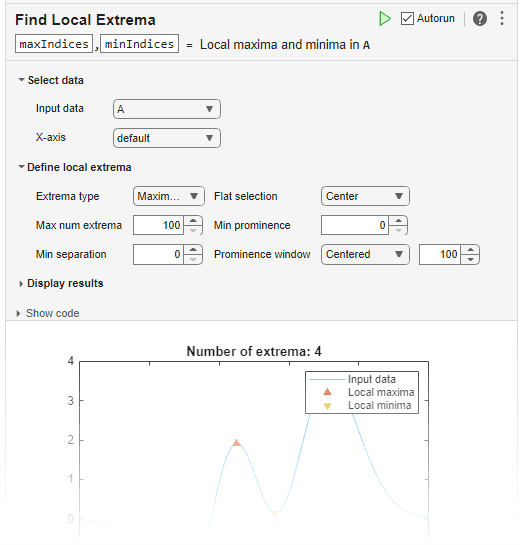
You can use islocalmax functionality interactively by adding the Find Local Extrema task to a live script.

TF = islocalmax(A,dim) specifies the dimension of A to operate along. For example, islocalmax(A,2) finds local maximum of each row of a matrix A.

TF = islocalmax(___,Name,Value) specifies parameters in addition to any of the input argument combinations in previous syntaxes for finding local maxima using one or more name-value arguments. For example, islocalmax(A,'SamplePoints',t) finds local maxima of A with respect to the time stamps contained in the time vector t.

[TF,P] = islocalmax(___) also returns the prominence corresponding to each element of A.

Examples

Local Maxima in Vector

Compute and plot the local maxima of a vector of data.

x = 1:100;
A = (1-cos(2*pi*0.01*x)).*sin(2*pi*0.15*x);
TF = islocalmax(A);
plot(x,A,x(TF),A(TF),'r*')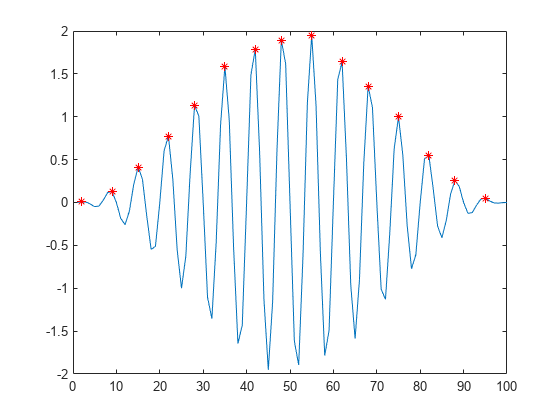

Maxima in Matrix Rows

Create a matrix of data, and compute the local maxima for each row.

A = 25*diag(ones(5,1)) + rand(5,5);
TF = islocalmax(A,2)

TF = 5×5 logical array

   0   0   1   0   0
   0   1   0   0   0
   0   0   1   0   0
   0   1   0   1   0
   0   1   0   0   0

Separated Maxima

Compute the local maxima of a vector of data relative to the time stamps in the vector t. Use the MinSeparation parameter to compute maxima that are at least 45 minutes apart.

t = hours(linspace(0,3,15));
A = [2 4 6 4 3 7 5 6 5 10 4 -1 -3 -2 0];
TF = islocalmax(A,'MinSeparation',minutes(45),'SamplePoints',t);
plot(t,A,t(TF),A(TF),'r*')

Flat Maxima Regions

Specify a method for indicating consecutive maxima values.

Compute the local maxima of data that contains consecutive maxima values. Indicate the maximum of each flat region based on the first occurrence of that value.

x = 0:0.1:5;
A = min(0.75, sin(pi*x));
TF1 = islocalmax(A,'FlatSelection','first');
plot(x,A,x(TF1),A(TF1),'r*')

Indicate the maximum of each flat region with all occurrences of that value.

TF2 = islocalmax(A,'FlatSelection','all');
plot(x,A,x(TF2),A(TF2),'r*')

Prominent Maxima

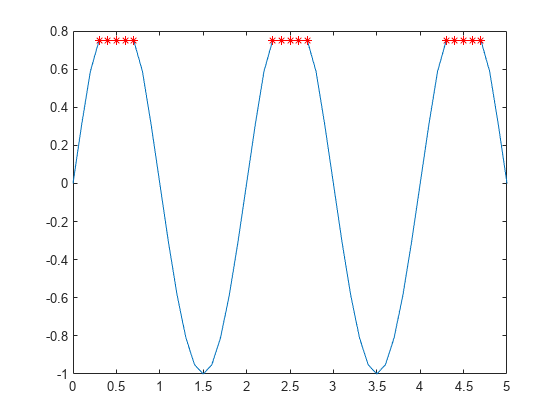
Select maxima based on their prominence.

Compute the local maxima of a vector of data and their prominence, and then plot them with the data.

x = 1:100;
A = peaks(100);
A = A(50,:);
[TF1,P] = islocalmax(A);
P(TF1)

ans = 1×2

    1.7703    3.5548

plot(x,A,x(TF1),A(TF1),'r*')
axis tight

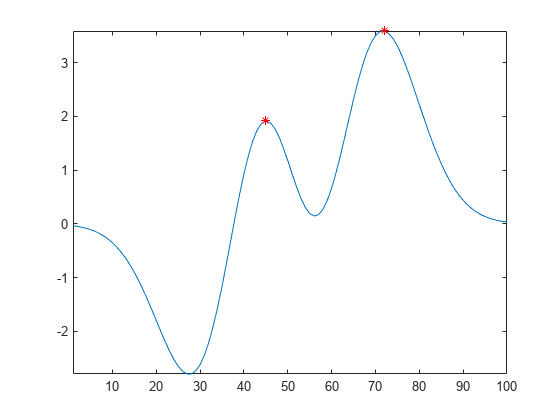
Compute only the most prominent maximum in the data by specifying a minimum prominence requirement.

TF2 = islocalmax(A,'MinProminence',2);
plot(x,A,x(TF2),A(TF2),'r*')
axis tight

Input Arguments

A — Input data

vector | matrix | multidimensional array | table | timetable

Input data, specified as a vector, matrix, multidimensional array, table, or timetable.

dim — Operating dimension

positive integer scalar

Operating dimension, specified as a positive integer scalar. If no value is specified, then the default is the first array dimension whose size does not equal 1.

Consider an m-by-n input matrix, A:

• islocalmax(A,1) computes local maxima according to the data in each column of A and returns an m-by-n matrix.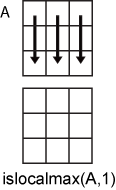

  

• islocalmax(A,2) computes local maxima according to the data in each row of A and returns an m-by-n matrix.

  

For table or timetable input data, dim is not supported and operation is along each table or timetable variable separately.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: TF = islocalmax(A,'MinProminence',2)

Data Options

SamplePoints — Sample points

vector | table variable name | scalar | function handle | table vartype subscript

Sample points, specified as a vector of sample point values or one of the options in the following table when the input data is a table. The sample points represent the x-axis locations of the data, and must be sorted and contain unique elements. Sample points do not need to be uniformly sampled. The vector [1 2 3 ...] is the default.

When the input data is a table, you can specify the sample points as a table variable using one of these options:

Indexing Scheme	Examples
Variable name: A string scalar or character vector	"A" or 'A' — A variable named A
Variable index: An index number that refers to the location of a variable in the table A logical vector. Typically, this vector is the same length as the number of variables, but you can omit trailing 0 or false values	3 — The third variable from the table [false false true] — The third variable
Function handle: A function handle that takes a table variable as input and returns a logical scalar	@isnumeric — One variable containing numeric values
Variable type: A vartype subscript that selects one variable of a specified type	vartype("numeric") — One variable containing numeric values

Note

This name-value argument is not supported when the input data is a timetable. Timetables use the vector of row times as the sample points. To use different sample points, you must edit the timetable so that the row times contain the desired sample points.

Example: islocalmax(A,'SamplePoints',0:0.1:10)

Example: islocalmax(T,'SamplePoints',"Var1")

DataVariables — Table variables to operate on

table variable name | scalar | vector | cell array | pattern | function handle | table vartype subscript

Table variables to operate on, specified as one of the options in this table. The DataVariables value indicates which variables of the input table to examine for local maxima. The data type associated with the indicated variables must be numeric or logical.

The first output TF contains false for variables not specified by DataVariables unless the value of OutputFormat is 'tabular'.

Indexing Scheme	Values to Specify	Examples
Variable name	A string scalar or character vector A string array or cell array of character vectors A pattern object	"A" or 'A' — A variable named A ["A" "B"] or {'A','B'} — Two variables named A and B "Var"+digitsPattern(1) — Variables named "Var" followed by a single digit
Variable index	An index number that refers to the location of a variable in the table A vector of numbers A logical vector. Typically, this vector is the same length as the number of variables, but you can omit trailing 0 (false) values.	3 — The third variable from the table [2 3] — The second and third variables from the table [false false true] — The third variable
Function handle	A function handle that takes a table variable as input and returns a logical scalar	@isnumeric — All the variables containing numeric values
Variable type	A vartype subscript that selects variables of a specified type	vartype("numeric") — All the variables containing numeric values

Example: islocalmax(T,'DataVariables',["Var1" "Var2" "Var4"])

OutputFormat — Output data type

'logical' (default) | 'tabular'

Output data type, specified as one of these values:

• 'logical' — For table or timetable input data, return the output TF as a logical array.

• 'tabular' — For table input data, return the output TF as a table. For timetable input data, return the output TF as a timetable.

For vector, matrix, or multidimensional array input data, OutputFormat is not supported.

Example: islocalmax(T,'OutputFormat','tabular')

Extrema Detection Options

MinProminence — Minimum prominence

0 (default) | nonnegative scalar

Minimum prominence, specified as a nonnegative scalar. islocalmax returns only local maxima whose prominence is at least the value specified.

ProminenceWindow — Prominence window

positive integer scalar | two-element vector of positive integers | positive duration scalar | two-element vector of positive durations

Prominence window, specified as a positive integer scalar, a two-element vector of positive integers, a positive duration scalar, or a two-element vector of positive durations. The value defines a window of neighboring points for which to compute the prominence for each local maximum.

When the window value is a positive integer scalar k, then the window is centered about each local maximum and contains k-1 neighboring elements. If k is even, then the window is centered about the current and previous elements. If a local maximum is within a flat region, then islocalmax treats the entire flat region as the center point of the window.

When the value is a two-element vector of positive integers[b f], then the window contains the local maximum, b elements backward, and f elements forward. If a local maximum is within a flat region, then the window starts b elements before the first point of the region and ends f elements after the last point of the region.

When the input data is a timetable or SamplePoints is specified as a datetime or duration vector, the window value must be of type duration, and the window is computed relative to the sample points.

FlatSelection — Flat region indicator

'center' (default) | 'first' | 'last' | 'all'

Flat region indicator for when a local maximum value is repeated consecutively, specified as one of these values:

• 'center' — Indicate only the center element of a flat region as the local maximum. The element of TF corresponding to the center of the flat is 1, and is 0 for the remaining flat elements.

• 'first' — Indicate only the first element of a flat region as the local maximum. The element of TF corresponding to the start of the flat is 1, and is 0 for the remaining flat elements.

• 'last' — Indicate only the last element of a flat region as the local maximum. The element of TF corresponding to the end of the flat is 1, and is 0 for the remaining flat elements.

• 'all' — Indicate all the elements of a flat region as the local maxima. The elements of TF corresponding to all parts of the flat are 1.

When using the MinSeparation or MaxNumExtrema name-value arguments, flat region points are jointly considered a single maximum point.

MinSeparation — Minimum separation

0 (default) | nonnegative scalar

Minimum separation between local maxima, specified as a nonnegative scalar. The separation value is defined in the same units as the sample points vector, which is [1 2 3 ...] by default. When the separation value is greater than 0, islocalmax selects the largest local maximum and ignores all other local maxima within the specified separation. This process is repeated until there are no more local maxima detected.

When the sample points vector has type datetime, the separation value must have type duration.

MaxNumExtrema — Maximum number of maxima

positive integer scalar

Maximum number of maxima, specified as a positive integer scalar. islocalmax finds no more than the specified number of the most prominent maxima, which is the length of the operating dimension by default.

Output Arguments

TF — Local maxima indicator

vector | matrix | multidimensional array | table | timetable

Local maxima indicator, returned as a vector, matrix, multidimensional array, table, or timetable.

TF is the same size as A unless the value of OutputFormat is 'tabular'. If the value of OutputFormat is 'tabular', then TF only has variables corresponding to the DataVariables specified.

Data Types: logical

P — Prominence

vector | matrix | multidimensional array | table | timetable

Prominence, returned as a vector, matrix, multidimensional array, table, or timetable.

• If P is a vector, matrix, or multidimensional array, P is the same size as A.

• If P is a table or timetable, P is the same height as A and only has variables corresponding to the DataVariables specified.

If the input data has a signed or unsigned integer type, then P is an unsigned integer.

Algorithms

islocalmax identifies all local maxima (or peaks) in the input data and follows these steps to compute the prominence of each local maximum. The prominence of a local maximum measures how the peak stands out with respect to its height and location relative to other peaks.

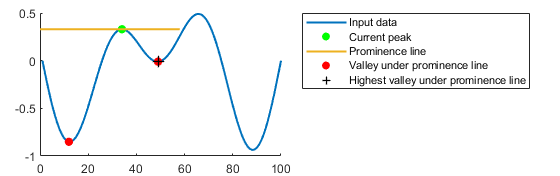
1. Draw a horizontal line to the left and right from the current peak. Stop drawing each segment of the horizontal line when it reaches the edge of the data or intersects the data.

2. Identify the valleys under the horizontal line.

3. Use the highest of those valleys as the basis value. The prominence is the absolute difference between the height of the current local maximum and the basis value.

Alternative Functionality

Live Editor Task

You can use islocalmax functionality interactively by adding the Find Local Extrema task to a live script.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

The islocalmax function supports tall arrays with the following usage notes and limitations:

• Tall timetables are not supported.

• You must specify a value for the ProminenceWindow name-value argument.

• The MaxNumExtrema, MinSeparation, and SamplePoints name-value arguments are not supported.

• The value of DataVariables cannot be a function handle.

For more information, see Tall Arrays.

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• You must enable support for variable-size arrays.

• The ProminenceWindow name-value argument is not supported.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The islocalmax function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2017b

R2022a: Return table or timetable containing logical output

For table or timetable input data, return a tabular output TF instead of a logical array by setting the OutputFormat name-value argument to 'tabular'.

R2021b: Specify sample points as table variable

For table input data, specify the sample points as a table variable using the SamplePoints name-value argument.