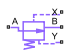
Pressure Compensator Valve (MA)

Pressure compensator valve in a moist air network

Since R2025a

• 

Libraries:
Simscape / Fluids / Moist Air / Valves & Orifices / Pressure Control Valves

Description

The Pressure Compensator Valve (MA) block represents a pressure compensator in an moist air network, such as a pressure relief valve or pressure-reducing valve. Use this valve to maintain the pressure at the valve based on signals from another part of the system. For more information about the valve parameterizations and block calculations, see the Orifice (MA) block.

The pressure differential between ports X and Y is the control pressure, P_control. When this value meets or exceeds the set pressure, the valve area opens or closes depending on the Valve specification parameter. The pressure regulation range begins at the set pressure, P_set. You can choose between constant and controlled set pressure regulation. A physical signal at port Ps provides a varying set pressure.

Pressure Control

The block regulates pressure when P_control exceeds P_set. The block continues to regulate the pressure up to P_max, the sum of P_set and the pressure regulation range. The block supports two modes of regulation:

• When you set Set pressure control to Controlled and connect a pressure signal to port Ps, the block keeps the pressure regulation range constant. The valve regulates pressure when P_control is greater than the value of the signal at port Ps and less than P_max.

• When you set Set pressure control to Constant, the Set pressure differential parameter defines a constant set pressure.

When you set Opening characteristic to Linear, the measure of flow capacity changes linearly between P_set and P_max.

When you set Opening characteristic to Tabulated, the measure of flow capacity changes with respect to the Opening pressure differential vector parameter.

Opening Dynamics

When you set Opening dynamics to On, the block introduces a control pressure lag and replaces p_control with the dynamic control pressure, p_dyn. The block calculates the dynamic control pressure based on the Opening time constant parameter, τ

$${\dot{p}}_{dyn}=\frac{p_{control}-p_{dyn}}{\tau }.$$

By default, the block does not model Opening dynamics. For the linear parameterization, a nonzero value for the Smoothing factor parameter provides additional numerical stability when the orifice is in near-closed or near-open position.

The block calculates the steady-state dynamics according to the Opening characteristic parameter, and are based on the control pressure, p_control.

Momentum Balance

The block equations depend on the Valve parameterization parameter. When you set Valve parameterization to Cv flow coefficient, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C_v\frac{S_{open}}{S_{Max}}{N}_{6}Y\sqrt{(p_{in}-p_{out}){\rho }_{in}},$$

where:

• C_v is the value of the Maximum Cv flow coefficient parameter.

• S_open is the valve opening area.

• S_Max is the maximum valve area when the valve is fully open.

• N₆ is a constant equal to 27.3 for mass flow rate in kg/hr, pressure in bar, and density in kg/m³.

• Y is the expansion factor.

• p_in is the inlet pressure.

• p_out is the outlet pressure.

• ρ_in is the inlet density.

The expansion factor is

$$Y=1-\frac{p_{in}-p_{out}}{3p_{in}{F}_{\gamma }{x}_T},$$

where:

• F_γ is the ratio of the isentropic exponent to 1.4.

• x_T is the value of the xT pressure differential ratio factor at choked flow parameter.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter, B_lam,

$$\dot{m}=C_v\frac{S_{open}}{S_{Max}}{N}_6{Y}_{lam}\sqrt{\frac{{\rho }_{avg}}{p_{avg}(1-B_{lam})}}(p_{in}-p_{out}),$$

where:

$$Y_{lam}=1-\frac{1-B_{lam}}{3F_{\gamma }{x}_T}.$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below $$1-F_{\gamma }{x}_T$$, the orifice becomes choked and the block switches to the equation

$$\dot{m}=\frac{2}{3}{C}_v\frac{S_{open}}{S_{Max}}{N}_6\sqrt{F_{\gamma }{x}_T{p}_{in}{\rho }_{in}}.$$

When you set Valve parameterization to Kv flow coefficient, the block uses these same equations, but replaces C_v with K_v by using the relation $$K_v=0.865C_v$$. For more information on the mass flow equations when the Valve parameterization parameter is Kv flow coefficient or Cv flow coefficient, [2][3].

When you set Valve parameterization to Sonic conductance, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}{p}_{in}\sqrt{\frac{T_{ref}}{T_{in}}}{\left[1-{\left(\frac{\frac{p_{out}}{p_{in}}-B_{crit}}{1-B_{crit}}\right)}^2\right]}^m,$$

where:

• C is the value of the Maximum sonic conductance parameter.

• B_crit is the critical pressure ratio.

• m is the value of the Subsonic index parameter.

• T_ref is the value of the ISO reference temperature parameter.

• ρ_ref is the value of the ISO reference density parameter.

• T_in is the inlet temperature.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter B_lam,

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}\sqrt{\frac{T_{ref}}{T_{avg}}}{\left[1-{\left(\frac{B_{lam}-B_{crit}}{1-B_{crit}}\right)}^2\right]}^m\left(\frac{p_{in}-p_{out}}{1-B_{lam}}\right).$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below the critical pressure ratio, B_crit, the orifice becomes choked and the block switches to the equation

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}{p}_{in}\sqrt{\frac{T_{ref}}{T_{in}}}.$$

The Sonic conductance setting of the Valve parameterization parameter is for pneumatic applications. If you use this setting for moist air with high levels of trace gasses or are modeling a fluid other than air, you may need to scale the sonic conductance by the square root of the mixture specific gravity.

For more information on the mass flow equations when the Valve parameterization parameter is Sonic conductance, see [1].

When you set Valve parameterization to Orifice area, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma -1}{p}_{in}{\rho }_{in}{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{2}{\gamma }}\left[\frac{1-{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{\gamma -1}{\gamma }}}{1-{\left(\frac{S_{open}}{S}\right)}^2{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{2}{\gamma }}}\right]},$$

where:

• S_open is the valve opening area.

• S is the value of the Cross-sectional area at ports A and B parameter.

• C_d is the value of the Discharge coefficient parameter.

• γ is the isentropic exponent.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter, B_lam,

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma -1}{p}_{avg}^{\frac{2-\gamma }{\gamma }}{\rho }_{avg}{B}_{lam}^{\frac{2}{\gamma }}\left[\frac{1-B_{lam}^{\frac{\gamma -1}{\gamma }}}{1-{\left(\frac{S_{open}}{S}\right)}^2{B}_{lam}^{\frac{2}{\gamma }}}\right]}\left(\frac{p_{in}^{\frac{\gamma -1}{\gamma }}-p_{out}^{\frac{\gamma -1}{\gamma }}}{1-B_{lam}^{\frac{\gamma -1}{\gamma }}}\right).$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below$${\left(\frac{2}{\gamma +1}\right)}^{\frac{\gamma }{\gamma -1}}$$ , the orifice becomes choked and the block switches to the equation

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma +1}{p}_{in}{\rho }_{in}\frac{1}{{\left(\frac{\gamma +1}{2}\right)}^{\frac{2}{\gamma -1}}-{\left(\frac{S_{open}}{S}\right)}^2}}.$$

For more information on the mass flow equations when the Valve parameterization parameter is Orifice area, see [4].

Mass Balance

The block conserves mass through the valve

$$\begin{array}{l}{\dot{m}}_A+{\dot{m}}_B=0\\ {\dot{m}}_{wA}+{\dot{m}}_{wB}=0\\ {\dot{m}}_{gA}+{\dot{m}}_{gB}=0\\ {\dot{m}}_{dA}+{\dot{m}}_{dB}=0\end{array}$$

where ṁ is the mass flow rate and the subscript w denotes water vapor, the subscript g denotes trace gas, and the subscript d denotes water droplets.

Energy Balance

The resistive element of the block is an adiabatic component. No heat exchange can occur between the fluid and the wall that surrounds it. No work is done on or by the fluid as it traverses from inlet to outlet. Energy can flow only by advection, through ports A and B. By the principle of conservation of energy, the sum of the port energy flows is always equal to zero

$${\varphi }_{\text{A}}+{\varphi }_{\text{B}}=0,$$

where ϕ is the energy flow rate into the valve through ports A or B.

Ports

Conserving

A — Moist air port

moist air

Moist air conserving port associated with the valve inlet.

B — Moist air port

moist air

Moist air conserving port associated with the valve outlet.

X — Pressure reference

moist air

Moist air conserving port associated with sensing the pressure at point X, P_x.

Y — Pressure reference

moist air

Moist air conserving port associated with sensing the pressure at point Y, P_y.

Input

Ps — Controlled pressure differential, Pa

physical signal

Pressure differential for controlled valve operation, in Pa.

Dependencies

To enable this port, set Set pressure control to Controlled.

Parameters

Valve parameterization — Model for valve parameterization

Cv flow coefficient (default) | Kv flow coefficient | Sonic conductance | Orifice area

Method the block uses to calculate the mass flow rate from the pressure difference across the valve or the pressure difference from the mass flow rate.

Opening characteristic — Method to convert from control signal to measure of flow capacity

Linear (default) | Tabulated

Method by which to parameterize the chosen measure of flow capacity.

Valve specification — Valve bias

Normally open (default) | Normally closed

Normal operating condition of the pressure compensator valve. For a reducing valve, choose Normally open valve. For a relief valve, choose Normally closed.

Set pressure control — Constant or controlled valve operation

Constant (default) | Controlled

Valve operation method. When you set this parameter to:

• Controlled and connect a pressure signal to port Ps, the block keeps the pressure regulation range constant. The valve regulates pressure when P_control is greater than the value of the signal at port Ps and less than P_max.

• Constant, the Set pressure differential parameter defines a constant set pressure.

Set pressure differential — Range outside of which constant valve operation is triggered

0 MPa (default) | scalar

Magnitude of the pressure differential that triggers pressure compensation.

Dependencies

To enable this parameter, set Set pressure control to Constant.

Pressure regulation range — Valve operational pressure range

0.1 MPa (default) | scalar

Operational pressure range of the valve. The pressure regulation range defines the difference between the Set pressure differential parameter and the maximum valve operating pressure.

Dependencies

To enable this parameter, set Opening characteristic to Linear.

Opening pressure differential vector — Differential pressure values for tabulated parameterization

[0.2 : 0.2 : 1.2] MPa (default) | 1-byn vector

Vector of pressure differential values for the tabulated parameterization of the opening area. The pressures must be in ascending order.

Dependencies

To enable this parameter, set Opening characteristic to Tabulated.

Maximum Cv flow coefficient — C_v coefficient that corresponds to maximally open component

4 (default) | positive scalar

Value of the C_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the vapor traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient and Opening characteristic to Linear.

Cv flow coefficient vector — C_v coefficients that correspond to values in member position vector

[1e-06, .8, 1.6, 2.4, 3.2, 4] (default) | 1-by-n vector

Vector of C_v flow coefficients. Each coefficient corresponds to a value in the Opening pressure (gauge) vector parameter. This parameter measures the ease with which the vapor traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient and Opening characteristic to Tabulated.

Maximum Kv flow coefficient — K_v coefficient that corresponds to maximally open component

3.6 (default) | positive scalar

Value of the K_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the vapor traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Kv flow coefficient and Opening characteristic to Linear.

Kv flow coefficient vector — K_v coefficients that correspond to values in member position vector

[1e-06, .72, 1.44, 2.16, 2.88, 3.6] (default) | 1-by-n vector

Vector of K_v flow coefficients. Each coefficient corresponds to a value in the Opening pressure (gauge) vector parameter. This parameter measures the ease with which the vapor traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Kv flow coefficient and Opening characteristic to Tabulated.

Maximum sonic conductance — Sonic conductance corresponding to maximally open component

12 l/(bar*s) (default) | positive scalar

Value of the sonic conductance when the control signal specified at port S is 1 and cross-sectional area available for flow is at a maximum.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance and Opening characteristic to Linear.

Critical pressure ratio — Ratio of downstream and upstream pressures at which the flow first chokes

0.3 (default) | positive scalar

Pressure ratio at which flow first begins to choke and the flow velocity reaches its maximum, given by the local speed of sound. The pressure ratio is the outlet pressure divided by inlet pressure.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance and Opening characteristic to Linear.

Subsonic index — Exponent used to characterize mass flow in subsonic flow regime

0.5 (default) | positive scalar

Empirical value used to more accurately calculate the mass flow rate in the subsonic flow regime.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference temperature — ISO 8778 reference temperature

293.15 K (default) | scalar

Temperature at standard reference atmosphere, defined as 293.15 K in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference density — ISO 8778 reference density

1.185 kg/m^3 (default) | positive scalar

Density at standard reference atmosphere, defined as 1.185 kg/m3 in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

Sonic conductance vector — Sonic conductances corresponding to values in control member position vector

[1e-05, 2.4, 4.8, 7.2, 9.6, 12] l/(bar*s) (default) | vector of positive values

Vector of sonic conductances inside the resistive element. The values in this vector correspond one-to-one with the elements in the Opening pressure (gauge) vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance and Opening characteristic to Tabulated.

Critical pressure ratio vector — Critical pressure ratios corresponding to values in control member position vector

0.3 * ones(1,6) (default) | vector of positive numbers

Vector of critical pressure ratios at which the flow first chokes. The critical pressure ratio is the fraction of downstream-to-upstream pressures at which the flow velocity reaches the local speed of sound. The values in this vector correspond one-to-one with the elements in Opening pressure (gauge) vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance and Opening characteristic to Tabulated.

xT pressure differential ratio factor at choked flow — Ratio of pressure differentials

0.7 (default) | positive scalar

Ratio between the inlet pressure, p_in, and the outlet pressure, p_out, defined as $$(p_{in}-p_{out})/p_{in}$$ where choking first occurs.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient or Kv flow coefficient.

Maximum orifice area — Maximum valve opening area

1e-4 m^2 (default) | positive scalar

Maximum valve area when the valve is fully open.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area and Opening characteristic to Linear.

Orifice area vector — Vector of valve opening area values

[1e-10, 2e-05, 4e-05, 6e-05, 8e-05, .0001] m^2 (default) | 1-by-n vector

Vector of orifice area values for the tabulated parameterization of the vapor valve area. The values in this vector correspond one-to-one with the elements in the Opening pressure (gauge) vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area and Opening characteristic to Tabulated.

Discharge coefficient — Discharge coefficient

0.64 (default) | positive scalar

Ratio of actual flow rate to ideal flow rate. This parameter accounts for real-world losses that are not captured in the orifice equation.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area.

Leakage flow fraction — Ratio of flow rates

1e-6 (default) | positive scalar

Ratio of the flow rate of the valve when it is closed to when it is open.

Dependencies

To enable this parameter, set Opening characteristic to Linear.

Smoothing factor — Numerical smoothing factor

0.01 (default) | positive scalar in the range [0,1]

Continuous smoothing factor that introduces a layer of gradual change to the flow response when the valve is in near-open or near-closed positions. Set this parameter to a nonzero value less than one to increase the stability of your simulation in these regions.

Dependencies

To enable this parameter, set Opening characteristic to Linear.

Laminar flow pressure ratio — Laminar-turbulent transition pressure ratio

0.999 (default) | positive scalar

Ratio of the valve outlet pressure to valve inlet pressure at which the fluid transitions between the laminar and turbulent regimes. The pressure loss corresponds to the mass flow rate linearly in laminar flows and quadratically in turbulent flows.

Cross-sectional area at ports A and B — Valve port areas

0.01 m^2 (default) | positive scalar

Area of the ports A and B.

Opening dynamics — Whether to account for flow response to valve opening

off (default) | on

Whether to account for transient effects to the fluid system due to the valve opening. Selecting this parameter approximates the opening conditions by introducing a first-order lag in the flow response.

Opening time constant — Valve opening time constant

0.1 s (default) | positive scalar

Time constant by which to compute the lag in the opening dynamics.

Dependencies

To enable this parameter, select Opening dynamics.

References

[1] ISO 6358-3, "Pneumatic fluid power – Determination of flow-rate characteristics of components using compressible fluids – Part 3: Method for calculating steady-state flow rate characteristics of systems", 2014.

[2] IEC 60534-2-3, “Industrial-process control valves – Part 2-3: Flow capacity – Test procedures”, 2015.

[3] ANSI/ISA-75.01.01, “Industrial-Process Control Valves – Part 2-1: Flow capacity – Sizing equations for fluid flow underinstalled conditions”, 2012.

[4] P. Beater, Pneumatic Drives, Springer-Verlag Berlin Heidelberg, 2007.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2025a