Poppet Valve (MA)

Poppet valve in a moist air network

Since R2025a

• 

Libraries:
Simscape / Fluids / Moist Air / Valves & Orifices / Flow Control Valves

Description

The Poppet Valve (MA) block represents an orifice with a translating ball that moderates flow through the valve. In the fully closed position, the ball rests at the perforated seat, and fully blocks the fluid from passing between ports A and B. The area between the ball and seat is the opening area of the valve.

The flow can be laminar or turbulent, and it can reach up to sonic speeds. The maximum velocity happens at the throat of the valve where the flow is narrowest and fastest. The flow chokes and the velocity saturates when a drop in downstream pressure can no longer increase the velocity. Choking occurs when the back-pressure ratio reaches the critical value characteristic of the valve. The block does not capture supersonic flow.

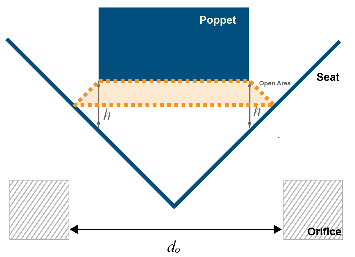
Cylindrical Stem Poppet Opening Area

The opening area of the valve is calculated as:

$$A_{open}=\pi h\sin \left(\frac{\theta }{2}\right)\left[d_s+\frac{h}{2}\sin \left(\theta \right)\right]+A_{leak},$$

where:

• h is the vertical distance between the outer edge of the cylinder and the seat, indicated in the schematic above.

• θ is the Seat cone angle.

• d_s is the Stem diameter.

• A_leak is the Leakage area.

The opening area is bounded by the maximum displacement h_max:

$$h_{\max }=\frac{d_s\left[\sqrt{1+\cos \left(\frac{\theta }{2}\right)}-1\right]}{\sin \left(\theta \right)}.$$

For any stem displacement larger than h_max, A_open is the sum of the maximum orifice area and the Leakage area:

$$A_{open}=\frac{\pi }{4}{d}_s^2+A_{leak}.$$

For any combination of the signal at port S and the cylinder offset less than 0, the minimum valve area is the Leakage area.

Round Ball Poppet Opening Area

Sharp-edged Seat Geometry

The opening area of the valve is calculated as:

$$A_{open,sharp-edged}=\pi r_O\sqrt{{\left(G_{sharp}+h\right)}^2+r_O^2}\left[1-\frac{r_B^2}{{\left(G_{sharp}+h\right)}^2+r_O^2}\right]+A_{leak},$$

where:

• h is the vertical distance between the outer edge of the cylinder and the seat, indicated in the schematic above.

• r_O is the seat orifice radius, calculated from the Orifice diameter.

• r_B is the radius of the ball, calculated from the Ball diameter.

• G_sharp is the geometric parameter: $$G_{sharp}=\sqrt{r_B^2-r_O^2}.$$

• A_leak is the Leakage area.

The opening area is bounded by the maximum displacement h_max:

$$h_{\max }=\sqrt{\frac{2r_B^2-r_O^2+r_O\sqrt{r_O^2+4r_B^2}}{2}}-G_{sharp}.$$

For any ball displacement larger than h_max, A_open is the sum of the maximum orifice area and the Leakage area:

$$A_{open}=\frac{\pi }{4}{d}_O^2+A_{leak}.$$

For any combination of the signal at port S and the ball offset that is less than 0, the minimum valve area is the Leakage area.

Conical Seat Geometry

The opening area of the valve is calculated as:

$$A_{open,conical}=G_{conical}h+\frac{\pi }{2}\sin \left(\theta \right)\sin \left(\frac{\theta }{2}\right)h^2+A_{leak},$$

where:

• h is the vertical distance between the outer edge of the cylinder and the seat, indicated in the schematic above.

• θ is the Seat cone angle.

• G_conical is the geometric parameter: $$G_{conical}=\pi r_B\sin \left(\theta \right),$$ where r_B is the ball radius.

• A_leak is the Leakage area.

The opening area is bounded by the maximum displacement h_max:

$$h_{\max }=\frac{\sqrt{r_B^2+\frac{r_O^2}{\cos \left(\frac{\theta }{2}\right)}}-r_B}{\sin \left(\frac{\theta }{2}\right)}.$$

For any ball displacement larger than h_max, A_open is the sum of the maximum orifice area and the Leakage area:

$$A_{open}=\frac{\pi }{4}{d}_O^2+A_{leak}.$$

For any combination of the signal at port S and the ball offset that is less than 0, the minimum valve area is the Leakage area.

Valve Parameterizations

The block behavior depends on the Valve parametrization parameter:

• Cv flow coefficient — The flow coefficient C_v determines the block parameterization. The flow coefficient measures the ease with which the moist air can flow when driven by a certain pressure differential.

• Kv flow coefficient — The flow coefficient K_v, where $$K_v=0.865C_v$$, determines the block parameterization. The flow coefficient measures the ease with which the moist air can flow when driven by a certain pressure differential.

• Sonic conductance — The sonic conductance of the resistive element at steady state determines the block parameterization. The sonic conductance measures the ease with which the moist air can flow when choked, which is a condition in which the flow velocity is at the local speed of sound. Choking occurs when the ratio between downstream and upstream pressures reaches a critical value known as the critical pressure ratio.

• Orifice area based on geometry — The size of the flow restriction determines the block parametrization.

The block scales the specified flow capacity by the fraction of valve opening. As the fraction of valve opening rises from 0 to 1, the measure of flow capacity scales from its specified minimum to its specified maximum.

Momentum Balance

The block equations depend on the Valve parameterization parameter. When you set Valve parameterization to Cv flow coefficient, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C_v\frac{S_{open}}{S_{Max}}{N}_{6}Y\sqrt{(p_{in}-p_{out}){\rho }_{in}},$$

where:

• C_v is the value of the Maximum Cv flow coefficient parameter.

• S_open is the valve opening area.

• S_Max is the maximum valve area when the valve is fully open.

• N₆ is a constant equal to 27.3 for mass flow rate in kg/hr, pressure in bar, and density in kg/m³.

• Y is the expansion factor.

• p_in is the inlet pressure.

• p_out is the outlet pressure.

• ρ_in is the inlet density.

The expansion factor is

$$Y=1-\frac{p_{in}-p_{out}}{3p_{in}{F}_{\gamma }{x}_T},$$

where:

• F_γ is the ratio of the isentropic exponent to 1.4.

• x_T is the value of the xT pressure differential ratio factor at choked flow parameter.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter, B_lam,

$$\dot{m}=C_v\frac{S_{open}}{S_{Max}}{N}_6{Y}_{lam}\sqrt{\frac{{\rho }_{avg}}{p_{avg}(1-B_{lam})}}(p_{in}-p_{out}),$$

where:

$$Y_{lam}=1-\frac{1-B_{lam}}{3F_{\gamma }{x}_T}.$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below $$1-F_{\gamma }{x}_T$$, the orifice becomes choked and the block switches to the equation

$$\dot{m}=\frac{2}{3}{C}_v\frac{S_{open}}{S_{Max}}{N}_6\sqrt{F_{\gamma }{x}_T{p}_{in}{\rho }_{in}}.$$

When you set Valve parameterization to Kv flow coefficient, the block uses these same equations, but replaces C_v with K_v by using the relation $$K_v=0.865C_v$$. For more information on the mass flow equations when the Valve parameterization parameter is Kv flow coefficient or Cv flow coefficient, [2][3].

When you set Valve parameterization to Sonic conductance, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}{p}_{in}\sqrt{\frac{T_{ref}}{T_{in}}}{\left[1-{\left(\frac{\frac{p_{out}}{p_{in}}-B_{crit}}{1-B_{crit}}\right)}^2\right]}^m,$$

where:

• C is the value of the Maximum sonic conductance parameter.

• B_crit is the critical pressure ratio.

• m is the value of the Subsonic index parameter.

• T_ref is the value of the ISO reference temperature parameter.

• ρ_ref is the value of the ISO reference density parameter.

• T_in is the inlet temperature.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter B_lam,

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}\sqrt{\frac{T_{ref}}{T_{avg}}}{\left[1-{\left(\frac{B_{lam}-B_{crit}}{1-B_{crit}}\right)}^2\right]}^m\left(\frac{p_{in}-p_{out}}{1-B_{lam}}\right).$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below the critical pressure ratio, B_crit, the orifice becomes choked and the block switches to the equation

$$\dot{m}=C\frac{S_{open}}{S_{Max}}{\rho }_{ref}{p}_{in}\sqrt{\frac{T_{ref}}{T_{in}}}.$$

The Sonic conductance setting of the Valve parameterization parameter is for pneumatic applications. If you use this setting for moist air with high levels of trace gasses or are modeling a fluid other than air, you may need to scale the sonic conductance by the square root of the mixture specific gravity.

For more information on the mass flow equations when the Valve parameterization parameter is Sonic conductance, see [1].

When you set Valve parameterization to Orifice area based on geometry, the mass flow rate, $$\dot{m}$$, is

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma -1}{p}_{in}{\rho }_{in}{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{2}{\gamma }}\left[\frac{1-{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{\gamma -1}{\gamma }}}{1-{\left(\frac{S_{open}}{S}\right)}^2{\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{2}{\gamma }}}\right]},$$

where:

• S_open is the valve opening area.

• S is the value of the Cross-sectional area at ports A and B parameter.

• C_d is the value of the Discharge coefficient parameter.

• γ is the isentropic exponent.

The block smoothly transitions to a linearized form of the equation when the pressure ratio, $$p_{out}/p_{in}$$, rises above the value of the Laminar flow pressure ratio parameter, B_lam,

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma -1}{p}_{avg}^{\frac{2-\gamma }{\gamma }}{\rho }_{avg}{B}_{lam}^{\frac{2}{\gamma }}\left[\frac{1-B_{lam}^{\frac{\gamma -1}{\gamma }}}{1-{\left(\frac{S_{open}}{S}\right)}^2{B}_{lam}^{\frac{2}{\gamma }}}\right]}\left(\frac{p_{in}^{\frac{\gamma -1}{\gamma }}-p_{out}^{\frac{\gamma -1}{\gamma }}}{1-B_{lam}^{\frac{\gamma -1}{\gamma }}}\right).$$

When the pressure ratio, $$p_{out}/p_{in}$$, falls below$${\left(\frac{2}{\gamma +1}\right)}^{\frac{\gamma }{\gamma -1}}$$ , the orifice becomes choked and the block switches to the equation

$$\dot{m}=C_d{S}_{open}\sqrt{\frac{2\gamma }{\gamma +1}{p}_{in}{\rho }_{in}\frac{1}{{\left(\frac{\gamma +1}{2}\right)}^{\frac{2}{\gamma -1}}-{\left(\frac{S_{open}}{S}\right)}^2}}.$$

For more information on the mass flow equations when the Valve parameterization parameter is Orifice area based on geometry, see [4].

Mass Balance

The block conserves mass through the valve

$$\begin{array}{l}{\dot{m}}_A+{\dot{m}}_B=0\\ {\dot{m}}_{wA}+{\dot{m}}_{wB}=0\\ {\dot{m}}_{gA}+{\dot{m}}_{gB}=0\\ {\dot{m}}_{dA}+{\dot{m}}_{dB}=0\end{array}$$

where ṁ is the mass flow rate and the subscript w denotes water vapor, the subscript g denotes trace gas, and the subscript d denotes water droplets.

Energy Balance

The resistive element of the block is an adiabatic component. No heat exchange can occur between the fluid and the wall that surrounds it. No work is done on or by the fluid as it traverses from inlet to outlet. Energy can flow only by advection, through ports A and B. By the principle of conservation of energy, the sum of the port energy flows is always equal to zero

$${\varphi }_{\text{A}}+{\varphi }_{\text{B}}=0,$$

where ϕ is the energy flow rate into the valve through ports A or B.

Assumptions and Limitations

• This block does not model supersonic flow.

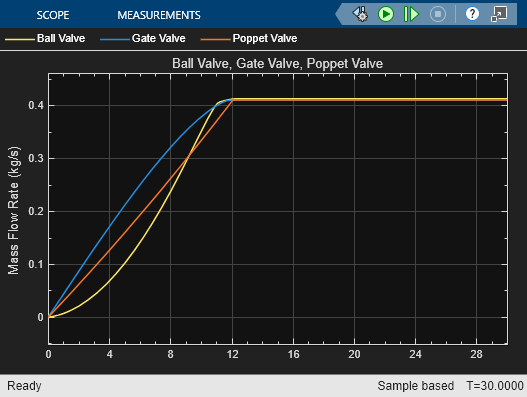
Examples

Compare Test Harnesses for Moist Air Flow Control Valves

This example uses test harnesses to compare the Ball Valve (MA), Gate Valve (MA), and Poppet Valve (MA) blocks. A test harness is a minimum viable model that you can use to parameterize blocks or isolate dynamics.

Model

Simulation Results from Scopes

This figure shows the mass flow rate through each of the valves. All three valves start closed and slowly open before reaching their maximum area. At the maximum area, the mass flow rate also reaches its maximum and cannot increase further. Each curve has a different profile while opening because each valve has a different area profile that depends on the valve geometry.

Ports

Conserving

A — Valve entry or exit

moist air

Liquid entry or exit port to the valve.

B — Valve entry or exit

moist air

Liquid entry or exit port to the valve.

Input

S — Stem displacement, m

physical signal

Displacement of the valve control member in m, specified as a physical signal.

Parameters

Poppet geometry — Type of poppet

Cylindrical stem (default) | Round ball

Type of poppet. You can choose either a cylindrical or ball-shaped control member.

Valve seat geometry — Geometry of valve seat

Sharp-edged (default) | Conical

Geometry of valve seat. The block uses this parameter to calculate the open area between the poppet and seat.

Dependencies

To enable this parameter, set Poppet geometry to Round ball.

Ball diameter — Diameter of ball control member

0.01 m (default) | positive scalar

Diameter of the ball control member.

Dependencies

To enable this parameter, set Poppet geometry to Round ball.

Orifice diameter — Seat orifice diameter

7e-3 m (default) | positive scalar

Seat orifice diameter.

Dependencies

To enable this parameter, set Poppet geometry to Round ball.

Stem diameter — Diameter of cylindrical stem

0.01 m (default) | positive scalar

Diameter of the cylindrical stem.

Dependencies

To enable this parameter, set Poppet geometry to Cylindrical stem.

Seat cone angle — Angle of seat opening

120 deg (default) | positive scalar

Angle of the seat opening.

Dependencies

To enable this parameter, set either:

• Poppet geometry to Cylindrical stem

• Poppet geometry to Round ball and Valve seat geometry to Conical

Control member position at closed orifice — Control member offset

0 m (default) | positive scalar

Poppet offset when valve is closed. A positive, nonzero value indicates a partially open valve. A negative, nonzero value indicates an overlapped valve that remains closed for an initial displacement set by the physical signal at port S.

Valve parameterization — Parameterization used to specify flow characteristics of orifice

Orifice area based on geometry (default) | Cv flow coefficient | Kv flow coefficient | Sonic conductance

Method to calculate the mass flow rate.

• Cv flow coefficient — The flow coefficient C_v determines the block parameterization.

• Kv flow coefficient — The flow coefficient K_v, where $$K_v=0.865C_v$$, determines the block parameterization.

• Sonic conductance — The sonic conductance of the resistive element at steady state determines the block parameterization.

• Orifice area based on geometry — The size of the flow restriction determines the block parametrization.

Discharge coefficient — Discharge coefficient

0.64 (default) | positive scalar in the range of [0,1]

Correction factor that accounts for discharge losses in theoretical flows.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area based on geometry.

Maximum Cv flow coefficient — Cv coefficient that corresponds to maximally open component

4 (default) | positive scalar

Value of the C_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the moist air traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient.

xT pressure differential ratio factor at choked flow — Ratio of pressure differentials

0.7 (default) | positive scalar

Ratio between the inlet pressure, p_in, and the outlet pressure, p_out, defined as $$(p_{in}-p_{out})/p_{in}$$ where choking first occurs. If you do not have this value, look it up in table 2 in ISA-75.01.01 [3]. Otherwise, the default value of 0.7 is reasonable for many valves.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient or Kv flow coefficient.

Maximum Kv flow coefficient — Kv coefficient that corresponds to maximally open component

3.6 (default) | positive scalar

Maximum value of the K_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the moist air traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Kv flow coefficient.

Maximum sonic conductance — Sonic conductance corresponding to maximally open component

12 l/(bar*s) (default) | positive scalar

Value of the sonic conductance when the cross-sectional area available for flow is at a maximum.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

Critical pressure ratio — Ratio of downstream and upstream pressures at which the flow first chokes

0.3 (default) | positive scalar

Pressure ratio at which flow first begins to choke and the flow velocity reaches its maximum, given by the local speed of sound. The pressure ratio is the outlet pressure divided by inlet pressure.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

Subsonic index — Exponent used to characterize mass flow in subsonic flow regime

0.5 (default) | positive scalar

Empirical value used to more accurately calculate the mass flow rate in the subsonic flow regime.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference temperature — ISO 8778 reference temperature

293.15 K (default) | scalar

Temperature at standard reference atmosphere, defined as 293.15 K in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference density — ISO 8778 reference density

1.185 kg/m^3 (default) | positive scalar

Density at standard reference atmosphere, defined as 1.185 kg/m3 in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

Leakage flow fraction — Ratio of flow rates

1e-6 (default) | positive scalar

Ratio of the flow rate of the orifice when it is closed to when it is open.

Smoothing factor — Numerical smoothing factor

0.01 (default) | positive scalar in the range [0,1]

Continuous smoothing factor that introduces a layer of gradual change to the flow response when the orifice is in near-open or near-closed positions. Set this parameter to a nonzero value less than one to increase the stability of your simulation in these regimes.

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes

0.999 (default) | positive scalar

Pressure ratio at which flow transitions between laminar and turbulent flow regimes. The pressure ratio is the outlet pressure divided by inlet pressure. Typical values range from 0.995 to 0.999.

Cross-sectional area at ports A and B — Flow area at moist air ports

0.01 m^2 (default) | positive scalar

Area normal to the flow path at each port. The ports are equal in size. The value of this parameter should match the inlet area of the components to which the resistive element connects.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2025a