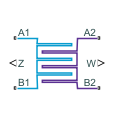
Condenser Evaporator (2P-MA)
Heat exchanger between moist air and two-phase fluid networks
Libraries:
Simscape /
Fluids /
Heat Exchangers /
Two-Phase Fluid - Moist Air
Description
The Condenser Evaporator (2P-MA) block models a heat exchanger with one moist air network, which flows between ports A2 and B2, and one two-phase fluid network, which flows between ports A1 and B1. The heat exchanger can act as a condenser or as an evaporator. The fluid streams can be aligned in parallel, counter, or cross-flow configurations.
Example Heat Exchanger for Refrigeration Applications

You can model the moist air side as flow within tubes, flow around the two-phase fluid tubing, or by an empirical, generic parameterization. The moist air side comprises air, trace gas, and water vapor that may condense throughout the heat exchange cycle. The block model accounts for energy transfer from the air to the liquid water condensation layer. This liquid layer does not collect on the heat transfer surface and is assumed to be completely removed from the downstream moist air flow. The humidity condensation rate is returned as a physical signal at port W.
The block uses the Effectiveness-NTU (E-NTU) method to model heat transfer through the shared wall. Fouling on the exchanger walls, which increases thermal resistance and reduces the heat exchange between the two fluids, is also modeled. You can also optionally model fins on both the moist air and two-phase fluid sides. Pressure loss due to viscous friction on both sides of the exchanger can be modeled analytically or by generic parameterization, which you can use to tune to your own data.
You can model the two-phase fluid side as flow within a tube or a set of tubes. The two-phase fluid tubes use a boundary-following model to track the sub-cooled liquid (L), vapor-liquid mixture (M), and super-heated vapor (V) in three zones. The relative amount of space a zone occupies in the system is called a zone length fraction within the system.
Zone Length Fractions in the Two-Phase Fluid Piping

The sum of the zone length fractions in the two-phase fluid tubing equals
1. Port Z returns the zone
length fractions as a vector of physical signals for each of the three phases: [L, M,
V].
Heat Exchanger Configuration
The heat exchanger effectiveness is based on the selected heat exchanger configuration, the fluid properties in each phase, the tube geometry and flow configuration on each side of the exchanger, and the usage and size of fins.
The Flow arrangement parameter assigns the relative flow paths between the two sides:
Parallel flowindicates the fluids are moving in the same direction.Counter flowindicates the fluids are moving in parallel, but opposite directions.Cross flowindicates the fluids are moving perpendicular to each other.
When Flow arrangement is set to Cross
flow, use the Cross flow arrangement
parameter to indicate whether the two-phase fluid or moist air flows are
separated into multiple paths by baffles or walls. Without these separations,
the flow can mix freely and is considered mixed. Both
fluids, one fluid, or neither fluid can be mixed in the cross-flow arrangement.
Mixing homogenizes the fluid temperature along the direction of flow of the
second fluid, and varies perpendicular to the second fluid flow.
Unmixed flows vary in temperature both along and perpendicular to the flow path of the second fluid.
Sample Cross-Flow Configurations
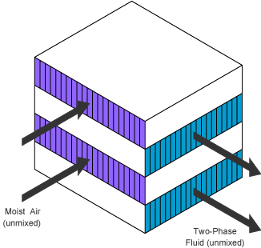
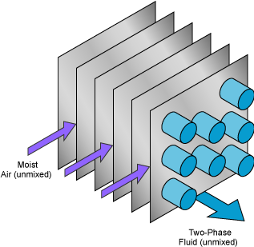
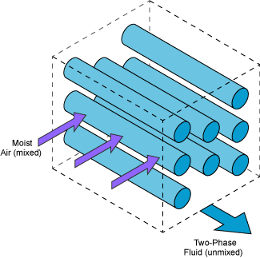
Note that the flow direction during simulation does not impact the selected flow arrangement setting. The ports on the block do not reflect the physical positions of the ports in the physical heat exchange system.
All flow arrangements are single-pass, which means that the fluids do not make multiple turns in the exchanger for additional points of heat transfer. To model a multi-pass heat exchanger, you can arrange multiple Condenser Evaporator (2P-MA) blocks in series or in parallel.
For example, to achieve a two-pass configuration on the two-phase fluid side and a single-pass configuration on the moist air side, you can connect the two-phase fluid sides in series and the moist air sides to the same input in parallel (such as two Mass Flow Rate Source blocks with half of the total mass flow rate), as shown below.
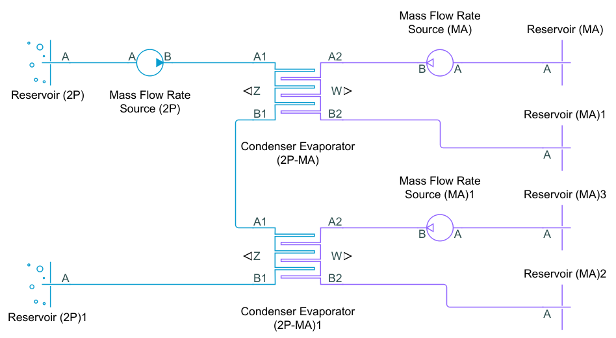
The Flow geometry parameter sets the moist air flow arrangement as either inside a tube or set of tubes, or perpendicular to a tube bank. You can also specify an empirical, generic configuration. The two-phase fluid always flows inside a tube or set of tubes.
When Flow geometry is set to Flow
perpendicular to bank of circular tubes, use the
Tube bank grid arrangement parameter to define the
two-phase fluid tube bank alignment as either Inline
or Staggered. The red, downward-pointing arrow
indicates the direction of moist air flow. Also indicated in the Inline figure
are the Number of tube rows along flow direction and the
Number of tube segments in each tube row parameters.
Here, flow direction refers to the moist air flow, and
tube refers to the two-phase fluid tubing. The
Length of each tube segment in a tube row parameter is
indicated in the Staggered figure.


The heat exchanger configuration does not have fins when the Total
fin surface area parameter is 0 m^2. Fins
introduce additional surface area for heat transfer. Each fluid side has a
separate fin area and parameters that describe the fins in that fluid. For
example, when the two-phase fluid flows inside the tubes and the moist air flows
outside of the tubes, the Total fin surface area and
Fin efficiency parameters in the Two-Phase
Fluid 1 section describe the fins protruding into the tube. The
Total fin surface area and Fin
efficiency parameters in the Moist Air 2
section describe the fins outside of the tubes.
Effectiveness-NTU Heat Transfer
The heat transfer rate is calculated for each fluid phase. In accordance with the three fluid zones that occur on the two-phase fluid side of the heat exchanger, the heat transfer rate is calculated in three sections.
The convective heat transfer in a zone is
where:
CMin is the lesser of the heat capacity rates of the two fluids in that zone. The heat capacity rate is the product of the fluid specific heat, cp, and the fluid mass flow rate. CMin is always positive.
TIn,2P is the zone inlet temperature of the two-phase fluid.
TIn,MA is the zone inlet temperature of the moist air.
ε is the heat exchanger effectiveness.
Effectiveness is a function of the heat capacity rate and the number of transfer units, NTU, and also varies based on the heat exchanger flow arrangement, which is discussed in more detail in Effectiveness by Flow Arrangement. The NTU is calculated as:
where:
z is the individual zone length fraction.
R is the total thermal resistance between the two flows, due to convection, conduction, and any fouling on the tube walls.
where:
U is the convective heat transfer coefficient of the respective fluid. This coefficient is discussed in more detail in Two-Phase Fluid Correlations and Moist Air Correlations.
F is the value of the Fouling factor parameter on the two-phase fluid or moist air side, respectively.
RW is the value of the Thermal resistance through heat transfer surface parameter.
ATh is the heat transfer surface area of the respective side of the exchanger. ATh is the sum of the wall surface area, AW, and the Total fin surface area, AF:
where ηF is the Fin efficiency.
The total convective heat transfer rate between the fluids is the sum of the heat transferred in the three zones by the subcooled liquid (QL), liquid-vapor mixture (QM), and superheated vapor (QV):
The fluid properties that the block uses in heat transfer calculations are the average between the value at the inlet and the value in the fluid volume.
The heat exchanger effectiveness varies according to its flow configuration and the mixing in each fluid. Below are the formulations for effectiveness calculated in the liquid and vapor zones for each configuration. The effectiveness is for all configurations in the mixture zone.
When Flow arrangement is set to
Parallel flow:When Flow arrangement is set to
Counter flow:When Flow arrangement is set to
Cross flowand Cross flow arrangement is set toBoth fluids unmixed:When Flow arrangement is set to
Cross flowand Cross flow arrangement is set toBoth fluids mixed:
When one fluid is mixed and the other unmixed, the equation for
effectiveness depends on the relative heat capacity rates of the fluids.
When Flow arrangement is set to Cross
flow and Cross flow arrangement
is set to either Two-Phase Fluid 1 mixed & Moist Air 2
unmixed or Two-Phase Fluid 1 unmixed
& Moist Air 2 mixed:
When the fluid with Cmax is mixed and the fluid with Cmin is unmixed:
When the fluid with Cmin is mixed and the fluid with Cmax is unmixed:
CR denotes the ratio between the heat capacity rates of the two fluids:
Conductive Heat Transfer
The conductive heat transfer in a zone is
where:
Tout,2P is the zone outlet temperature of the two-phase fluid.
Tout,MA is the zone outlet temperature of the moist air.
Rcond is the total conductive thermal resistance between the two flows,
where:
AW is the wall surface area.
k is the thermal conductivity of each fluid.
DH is the hydraulic diameter.
The total heat transfer is the sum of the convective and conductive heat transfer. The conductive heat transfer is negligible compared to the convective heat transfer. When the flow rate is zero, the convective heat transfer is also zero. However, because heat transfer from convection and conduction operate independently of each other, there is still conductive heat transfer even when the convective heat transfer is zero.
Condensation
On the moist air side, a layer of condensation may form on the heat transfer surface. This liquid layer can influence the amount of heat transferred between the moist air and two-phase fluid. The equations for E-NTU heat transfer above are given for dry heat transfer. To correct for the influence of condensation, the E-NTU equations are additionally calculated with the wet parameters listed below. Whichever of the two calculated heat flow rates results in a larger amount of moist air side cooling is used in heat calculations [1][2]. To use this method, the Lewis number is assumed to be close to 1, which is true for moist air [1][2].
E-NTU Quantities Used for Heat Transfer Rate Calculations
| Dry calculation | Wet calculation | |
|---|---|---|
| Moist air zone inlet temperature | Tin,MA | Tin,wb,MA |
| Heat capacity rate | ||
| Heat transfer coefficient | UMA |
where:
Tin,MA is the moist air zone inlet temperature.
Tin,wb,MA is the moist air wet-bulb temperature associated with Tin,MA.
is the dry air mass flow rate.
is the moist air heat capacity per unit mass of dry air.
is the equivalent heat capacity. The equivalent heat capacity is the change in the moist air specific enthalpy (per unit of dry air), , with respect to temperature at saturated moist air conditions:
The mass flow rate of the condensed water vapor leaving the moist air mass flow depends on the relative humidity between the moist air inlet and the channel wall and the heat exchanger NTUs:
where:
Wwall,MA is the humidity ratio at the heat transfer surface.
Win,MA is the humidity ratio at the moist air flow inlet.
NTUMA is the number of transfer units on the moist air side, calculated as:
The energy flow associated with water vapor condensation is based on the difference between the vapor specific enthalpy, hwater, wall, and the specific enthalpy of vaporization, hfg, for water:
The condensate is assumed to not accumulate on the heat transfer surface, and does not influence geometric parameters such as tube diameter. The condensed water is assumed to be completely removed from the downstream moist air flow.
Two-Phase Fluid Correlations
The convective heat transfer coefficient varies according to the fluid Nusselt number:
where:
Nu is the zone mean Nusselt number, which depends on the flow regime.
k is the fluid phase thermal conductivity.
DH is tube hydraulic diameter.
For turbulent flows in the subcooled liquid or superheated vapor zones, the Nusselt number is calculated with the Gnielinski correlation:
where:
Re is the fluid Reynolds number.
Pr is the fluid Prandtl number.
For turbulent flows in the liquid-vapor mixture zone, the Nusselt number is calculated with the Cavallini-Zecchin correlation:
where:
ReSL is the Reynolds number of the saturated liquid.
PrSL is the Prandtl number of the saturated liquid.
ρSL is the density of the saturated liquid.
ρSV is the density of the saturated vapor.
a= 0.05, b = 0.8, and c= 0.33.
For laminar flows, the Nusselt number is set by the Laminar flow Nusselt number parameter.
For transitional flows, the Nusselt number is a blend between the laminar and turbulent Nusselt numbers.
When the Heat transfer coefficient model parameter is
Colburn equation, the block calculates the
Nusselt number for the subcooled liquid and superheated vapor zones by using the
empirical Colburn equation
where a, b, and c are values in the Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone and Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone parameters.
The block calculates the Nusselt number for liquid-vapor mixture zones by using the Cavallini-Zecchin equation with the variables in the Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone parameter.
The pressure loss due to viscous friction varies depending on flow regime and
configuration. The pressure loss calculation uses the overall density, which is
the total fluid mass divided by the total fluid volume. When the
Pressure loss model parameter is
Correlation for flow inside tubes, the pressure
loss due to friction depends on the Darcy friction factor.
For turbulent flows, when the Reynolds number is above the Turbulent flow lower Reynolds number limit parameter, the block calculates the pressure loss due to friction in terms of a calculated Darcy friction factor. The pressure differential between port A1 and the internal node I1 is:
where:
A1 is the total flow rate through port A1.
fD,A is the Darcy friction factor according to the Haaland correlation. When the Local resistance specification parameter is
Aggregate equivalent length,where εR is the value of the Internal surface absolute roughness parameter. The friction factor is dependent on the Reynolds number, and the block calculates this value at both ports for each liquid.
L is the value of the Total length of each tube parameter.
LAdd is the value of the Aggregate equivalent length of local resistances parameter, which is the equivalent length of a tube that introduces the same amount of loss as the sum of the losses due to other local resistances in the tube.
ACS is the tube cross-sectional area.
The pressure differential between port B1 and internal node I1 is:
where B1 is the total flow rate through port B1.
When the Local resistance specification parameter is
Aggregate equivalent length, the Darcy friction
factor at port B1 is:
When the Local resistance specification parameter is
Local loss coefficient, the Darcy friction
factors at ports A1 and B1 are
where Clocalloss is the value of the Total local loss coefficient parameter.
For laminar flows, when the Reynolds number is below the Laminar
flow upper Reynolds number limit parameter, the block calculates
the pressure loss due to friction in terms of the Laminar friction
constant for Darcy friction factor parameter,
λ. λ is a user-defined parameter when
Tube cross-section is
Generic. Otherwise, the block calculates the
value internally. The pressure differential between port A1
and internal node I1 is:
where μ is the fluid dynamic viscosity. The pressure differential between port B1 and internal node I1 is:
For transitional flows, the pressure differential due to viscous friction is a smoothed blend between the values for laminar and turbulent pressure losses.
When Pressure loss model is set to Pressure
loss coefficient, the pressure losses due to viscous friction
are calculated with an empirical pressure loss coefficient,
ξ.
The pressure differential between port A1 and internal node I1 is:
The pressure differential between port B1 and internal node I1 is:
Moist Air Correlations
When the moist air Flow geometry is set to
Flow inside one or more tubes, the Nusselt number
is calculated according to the Gnielinski correlation in the same manner as
two-phase supercooled liquid or superheated vapor. See Heat Transfer Coefficient for more
information.
When the moist air Flow geometry is set to
Flow perpendicular to bank of circular tubes, the
Nusselt number is calculated based on the Hagen number, Hg, and depends on the
Tube bank grid arrangement setting:
where:
D is the Tube outer diameter.
lL is the Longitudinal tube pitch (along flow direction), the distance between the tube centers along the flow direction. Flow direction refers to the moist air flow.
lT is the Transverse tube pitch (perpendicular to flow direction), shown in the figure below. The transverse pitch is the distance between the centers of the two-phase fluid tubing in one row.
lD is the diagonal tube spacing, calculated as
For more information on calculating the Hagen number, see [6].
The longitudinal and transverse pitch distances are the same for both grid bank arrangement types.
Cross-Section of Two-Phase Fluid Tubing with Pitch Measurements


When the Heat transfer coefficient model is set to
Colburn equation or when Flow
geometry is set to Generic, the
Nusselt number is calculated by the empirical Colburn equation:
where a, b, and c are the values defined in the Coefficients [a, b, c] for a*Re^b*Pr^c parameter.
When the moist air Flow geometry is set to
Flow inside one or more tubes, the pressure loss
is calculated the same way as for two-phase flows, with the respective Darcy
friction factor, density, mass flow rates, and pipe lengths of the moist air
side. See Pressure Loss for more
information.
When the moist air Flow geometry is set to
Flow perpendicular to bank of circular tubes, the
Hagen number is used to calculate the pressure loss due to viscous friction. The
pressure differential between port A2 and internal node I2 is:
where:
μMA is the fluid dynamic viscosity.
NR is the Number of tube rows along flow direction. This is the number of two-phase fluid tube rows along the moist air flow direction.
The pressure differential between port B2 and internal node I2 is:
When the Pressure loss model is set to Euler
number per tube row or when Flow geometry
is set to Generic, the pressure loss due to viscous
friction is calculated with a pressure loss coefficient, in terms of the Euler
number, Eu:
where ξ is the empirical pressure loss coefficient.
The pressure differential between port A2 and internal node I2 is:
The pressure differential between port B2 and internal node I2 is:
Wall Thermal Mass
If you select Enable wall thermal mass, the block models the heat exchanger wall thermal mass, which introduces a delay in the wall's transient response to changes in temperature or heat flux. If you model thermal mass, the wall stores heat in its bounds. This heat storage slows the transition between steady states so that a thermal perturbation on one side does not immediately manifest on the other side. The lag persists until the heat flow rates from the two sides balance.
If you select Enable wall thermal mass, the wall energy conservation is
where:
Mwall is the value of the Wall mass parameter.
cp,wall is the value of the Wall specific heat parameter.
Twall is the effective wall temperature on each side. The block uses this value to model the transient response. You cannot measure this value.
The heat transfer to each fluid is
where:
Tin is the fluid inlet temperature on each side.
C is the heat capacity rate for each fluid.
The number of heat transfer units between the fluid and the wall on each side is
where A is the wall surface area and U is the heat transfer coefficient.
Conservation Equations
The total mass accumulation rate in the two-phase fluid is defined as:
where:
M2P is the total mass of the two-phase fluid.
A1 is the mass flow rate of the fluid at port A1.
B1 is the mass flow rate of the fluid at port B1.
The flow is positive when flowing into the block through the port.
The energy conservation equation relates the change in specific internal energy to the heat transfer by the fluid:
where:
u2P is the two-phase fluid specific internal energy.
φA1 is the energy flow rate at port A1.
φB1 is the energy flow rate at port B1.
Q is heat transfer rate, which is positive when leaving the two-phase fluid volume.
The block has mass conversion equations for the moist air mixture, water vapor, trace gas, and water droplets.
Note
If the Trace gas model parameter is
None in the Moist Air Properties (MA) block, the moist air
network does not model trace gas. In this case, in the Condenser Evaporator (2P-MA)
block, the conservation equation for trace gas is set to 0.
If you clear the Enable entrained water droplets in the Moist Air Properties (MA) block, the moist air network does not model entrained water droplets. In this case, in the Condenser Evaporator (2P-MA) block, the conservation equation for water droplets is set to 0.
The accumulation rate for the moist air mixture accounts for the changes of the moist air mass flow through the exchanger ports and the condensation mass flow rate,
where:
A2 is the moist air mass flow rate at port A2.
A2 is the moist air mass flow rate at port B2.
w,cond is the rate of water vapor condensation due to a saturated fluid volume.
w,conv is the rate of condensation on the wall surface.
d,evap is the rate of water droplet evaporation.
The mass conservation equation for water vapor is
where xw is the mass fraction of the vapor, ρMAI is the density of the moist air in the fluid volume, and V is the total moist air volume.
w,net is the net water vapor mass flow rate,
where:
is the water vapor mass flow rate at port A2.
is the water vapor mass flow rate at port B2.
The trace gas mass balance is
where:
xg is the mass fraction of the trace gas.
is the trace gas mass flow rate at port A2.
is the trace gas mass flow rate at port B2.
The water droplet mass balance is
where rdI is the mass ratio of the water droplets to the moist air in the fluid volume.
is the net water droplet mass flow rate,
where:
d,A2 is the water droplets mass flow rate at port A2.
d,A2 is the water droplets mass flow rate at port B2.
λd is the value of the Fraction of condensate entrained as water droplets parameter.
On the moist air side, energy conservation accounts for the change in specific internal energy due to heat transfer and water vapor condensing out of the moist air mass,
where:
ua,I, uw,I, and ug,I are the internal energies of the air, water vapor, and gas, respectively.
cpI is the moist air specific heat.
cpdI is the water droplet specific heat.
rd is the mass ratio of water droplets to moist air.
pI is the pressure of the internal volume.
TI is the temperature of the internal volume.
RI is the internal volume specific gas constant.
hdI is the water droplet specific enthalpy in the fluid volume.
hdH is the water droplet specific enthalpy on the wall surface.
ϕA2 is the energy flow rate at port A2.
ϕB2 is the energy flow rate at port B2.
The heat transferred to or from the moist air, Q, is equal to the heat transferred from or to the thermal liquid.
Examples
Ports
Conserving
Output
Parameters
References
[1] 2013 ASHRAE Handbook - Fundamentals. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., 2013.
[2] Braun, J. E., S. A. Klein, and J. W. Mitchell. "Effectiveness Models for Cooling Towers and Cooling Coils." ASHRAE Transactions 95, no. 2, (June 1989): 164–174.
[3] Çengel, Yunus A. Heat and Mass Transfer: A Practical Approach. 3rd ed, McGraw-Hill, 2007.
[4] Ding, X., Eppe J.P., Lebrun, J., Wasacz, M. "Cooling Coil Model to be Used in Transient and/or Wet Regimes. Theoretical Analysis and Experimental Validation." Proceedings of the Third International Conference on System Simulation in Buildings (1990): 405-411.
[5] Mitchell, John W., and James E. Braun. Principles of Heating, Ventilation, and Air Conditioning in Buildings. Wiley, 2013.
[6] Shah, R. K., and Dušan P. Sekulić. Fundamentals of Heat Exchanger Design. John Wiley & Sons, 2003.
[7] White, Frank M. Fluid Mechanics. 6th ed, McGraw-Hill, 2009.