fuzarith

Perform fuzzy arithmetic

Syntax

C = fuzarith(X,A,B,operator)

Description

C = fuzarith(X,A,B,operator) returns the fuzzy set C, which is the result of applying the specified fuzzy operator to the fuzzy sets A and B. The operation is performed across the universe of discourse X

Examples

Perform Fuzzy Arithmetic

Specify Gaussian and trapezoidal membership functions.

N = 501;
minX = -20;
maxX = 20;
x = linspace(minX,maxX,N);

A = trapmf(x,[-10 -2 1 3]);
B = gaussmf(x,[2 5]);

Evaluate the sum, difference, product, and quotient of A and B.

Csum = fuzarith(x,A,B,"sum");
Csub = fuzarith(x,A,B,"sub");
Cprod = fuzarith(x,A,B,"prod");
Cdiv = fuzarith(x,A,B,"div");

Plot the addition and subtraction results.

figure
subplot(2,1,1)
plot(x,A,"--",x,B,":",x,Csum,"c")
title("Fuzzy Addition, A+B")
legend("A","B","A+B")
subplot(2,1,2)
plot(x,A,"--",x,B,":",x,Csub,"c")
title("Fuzzy Subtraction, A-B")
legend("A","B","A-B")

Plot the multiplication and division results.

figure
subplot(2,1,1)
plot(x,A,"--",x,B,":",x,Cprod,"c")
title("Fuzzy Multiplication, A*B")
legend("A","B","A*B")
subplot(2,1,2)
plot(x,A,"--",x,B,":",x,Cdiv,"c")
title("Fuzzy Division, A/B")
legend("A","B","A/B")

Input Arguments

X — Universe of discourse

vector

Universe of discourse, specified as a vector.

A — Input fuzzy set

vector

Input fuzzy set, specified as a vector with the same length as X. Each element of A is the value of the fuzzy set for the corresponding value of X.

A must be a convex fuzzy set. For more information, see Algorithms.

B — Input fuzzy set

vector

Input fuzzy set, specified as a vector with the same length as X. Each element of B is the value of the fuzzy set for the corresponding value of X.

B must be a convex fuzzy set. For more information, see Algorithms.

operator — Fuzzy arithmetic operator

"sum" | "sub" | "prod" | "div"

Arithmetic operator, specified as one of these values:

• "sum" — Fuzzy addition

• "sub" — Fuzzy subtraction

• "prod" — Fuzzy multiplication

• "div" — Fuzzy division

For more information on fuzzy arithmetic operations, see Algorithms.

Output Arguments

C — Output fuzzy set

column vector

Output fuzzy set, returned as a column vector with length equal to the length of X.

Algorithms

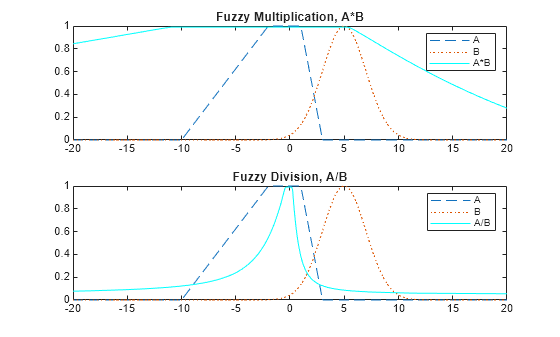
To perform fuzzy arithmetic operations, the fuzzy operands (input fuzzy sets A and B) must be convex fuzzy sets. A fuzzy set is convex if, for each pair of points x₁ and x₂ in the universe of discourse X and λ∈[0,1].

$$\mu \left(\lambda x_1+\left(1-\lambda \right)x_2\right)\ge \min \left(\mu \left(x_1\right),\mu \left(x_2\right)\right)$$

An α-cut of a fuzzy set is the region in the universe of discourse for which the fuzzy set has a specific membership value, α. For a convex fuzzy set, every α-cut defines a continuous region in the universe of discourse.

fuzarith uses the continuous regions defined by the α-cuts of fuzzy sets A and B to compute the corresponding α-cut of the output fuzzy set C. To do so, fuzarith uses interval arithmetic.

The following table shows how to compute the left and right boundaries of the output interval. Here:

• [A_L A_R] is the interval defined by the α-cut of fuzzy set A.

• [B_L B_R] is the interval defined by the α-cut of fuzzy set B.

• [C_L C_R] is the interval defined by the α-cut of fuzzy set C.

Interval Arithmetic Operator	Definition
Addition: C = A+B	$$\begin{array}{l}{C}_L=A_L+B_L\\ C_R=A_R+B_R\end{array}$$
Subtraction: C = A-B	$$\begin{array}{l}{C}_L=A_L-B_R\\ C_R=A_R-B_L\end{array}$$
Multiplication: C = A*B	$$\begin{array}{l}{C}_L=\min \left(A_L\cdot B_L,A_L\cdot B_R,A_R\cdot B_L,A_R\cdot B_R\right)\\ C_R=\max \left(A_L\cdot B_L,A_L\cdot B_R,A_R\cdot B_L,A_R\cdot B_R\right)\end{array}$$
Division: C = A/B	$$\begin{array}{l}{C}_L=\min \left(\frac{A_L}{B_L},\frac{A_L}{B_R},\frac{A_R}{B_L},\frac{A_R}{B_R}\right)\\ C_R=\max \left(\frac{A_L}{B_L},\frac{A_L}{B_R},\frac{A_R}{B_L},\frac{A_R}{B_R}\right)\end{array}$$ fuzarith removes invalid intervals for divisor B. Interval [BL,BR] is invalid if it includes zero.

Version History

Introduced before R2006a