Foundations of Fuzzy Logic
Overview
The point of fuzzy logic is to map an input space to an output space. The primary mechanism for doing this is a list of if-then statements called rules. All rules are evaluated in parallel and the order of the rules is unimportant. The rules themselves are useful because they refer to variables and the adjectives that describe those variables. Before you can build a system that interprets rules, you must define all the terms you plan on using and the adjectives that describe them. To say that the water is hot, you need to define the range within which the water temperature can be expected to vary as well as what you mean by the word hot.
In general, fuzzy inference is a method that interprets the values in the input vector and, based on some set of rules, assigns values to the output vector.
Fuzzy Sets
Fuzzy logic starts with the concept of a fuzzy set. A fuzzy set is a set without a crisp, clearly defined boundary. It can contain elements with only a partial degree of membership.
To understand what a fuzzy set is, first consider the definition of a classical set. A classical set is a container that wholly includes or wholly excludes any given element. For example, the set of days of the week unquestionably includes Monday, Thursday, and Saturday. It just as unquestionably excludes butter, liberty, dorsal fins, and so on.
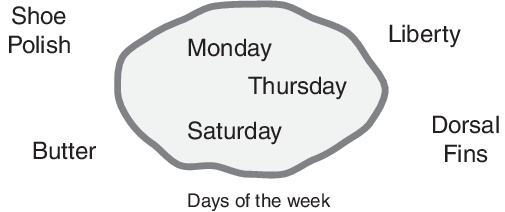
This type of set is called a classical set. Such sets follow the Law of the Excluded Middle — X must either be in set A or in set not-A. That is, the two categories A and not-A, should between them contain the entire universe of discourse.
Now, consider the set of days comprising a weekend. The following figure attempts to classify the weekend days.
Most people would agree that Saturday and Sunday belong in the weekend set, but what about Friday? It feels like a part of the weekend, but somehow it seems like it should be technically excluded. Therefore, Friday "straddles the fence." Classical sets do not support this kind of classification. Either something is in a set or it is out of a set. However, human experience suggests something different — straddling the fence is part of life.

Individual perceptions and cultural background must be taken into account when you define what constitutes the weekend. Even the dictionary is imprecise, defining the weekend as the period from Friday night or Saturday to Monday morning.
For such situations, sharp-edged, yes-no logic can be less helpful, whereas fuzzy reasoning becomes more helpful.
In fuzzy logic, the truth of any statement is a matter of degree. The major advantage that fuzzy reasoning offers is the ability to reply to a yes-no question with a not-quite-yes-or-no answer.
Reasoning in fuzzy logic is a matter of generalizing the familiar yes-no (Boolean) logic. If you give true the numerical value of 1 and false the numerical value of 0, fuzzy logic then permits in-between values like 0.2 and 0.7453. For instance:
| Q: Is Saturday a weekend day? |
| A: 1 (yes, or true) |
| Q: Is Tuesday a weekend day? |
| A: 0 (no, or false) |
| Q: Is Friday a weekend day? |
| A: 0.8 (for the most part yes, but not completely) |
| Q: Is Sunday a weekend day? |
| A: 0.95 (yes, but not quite as much as Saturday). |
The plot on the left shows the truth values for weekend-ness if you are forced to respond with an absolute yes or no response. On the right is a plot that shows the truth value for weekend-ness if you are allowed to respond with fuzzy in-between values.
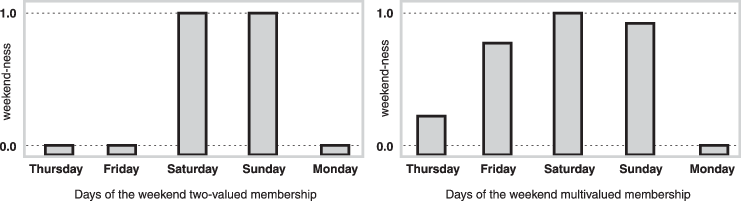
Technically, the representation on the right is from the domain of multivalued logic (or multivalent logic). If you ask the question "Is X a member of set A?" the answer might be yes, no, or any one of a thousand intermediate values in between. Thus, X might have partial membership in A. Multivalued logic stands in direct contrast to the more familiar concept of two-valued (or bivalent yes-no) logic.
Consider the continuous-scale time plot of weekend-ness shown in the following figure.

By making the plot continuous, you define the degree to which any given instant belongs in the weekend rather than an entire day. In the plot on the left, at midnight on Friday, the weekend-ness truth value jumps discontinuously from 0 to 1.
The plot on the right shows a smoothly varying curve that accounts for the fact that all of Friday, and, to a small degree, parts of Thursday, partake of the quality of weekend-ness and thus deserve partial membership in the fuzzy set of weekend moments. The curve that defines the weekend-ness of any instant in time is a function that maps the input space (time of the week) to the output space (weekend-ness). Such a function is a membership function.
As another example of fuzzy sets, consider the question of seasons. What season is it right now? In the northern hemisphere, summer officially begins at the exact moment in the earth's orbit when the North Pole is pointed most directly toward the sun. It occurs exactly once a year, in late June. Using the astronomical definitions for the season, you get sharp boundaries as shown on the left in the figure that follows. But what you experience as the seasons vary continuously as shown on the right in the following figure (in temperate northern hemisphere climates).

Membership Functions
A membership function (MF) is a curve that defines how each point in the input space is mapped to a membership value (or degree of membership) between 0 and 1. The input space is often referred to as the universe of discourse.
One of the most commonly used examples of a fuzzy set is the set of tall people. In this case, the universe of discourse is all potential heights, say from three feet to nine feet. The word tall corresponds to a curve that defines the degree to which any person is tall. If the set of tall people is given the well-defined (crisp) boundary of a classical set, you might say all people taller than six feet are officially considered tall. However, it is unreasonable to call one person short and another one tall when they differ in height by an inch.

If the kind of distinction shown previously is unworkable, then what is the right way to define the set of tall people? Much as with the plot of weekend days, the following figure shows a smoothly varying curve that passes from not-tall to tall. The output axis is a number known as the membership value between 0 and 1. The curve is known as a membership function and is often given the designation of µ. For example, the following figure shows both crisp and smooth tall membership functions. In the top plot, the two people are classified as either entirely tall or entirely not-tall. In the bottom plot, the smooth transition allows for different degrees of tallness. Both people are tall to some degree, but one is significantly less tall than the other. The taller person, with a tallness membership of 0.95 is definitely a tall person, but the person with a tallness membership of 0.3 is not very tall.
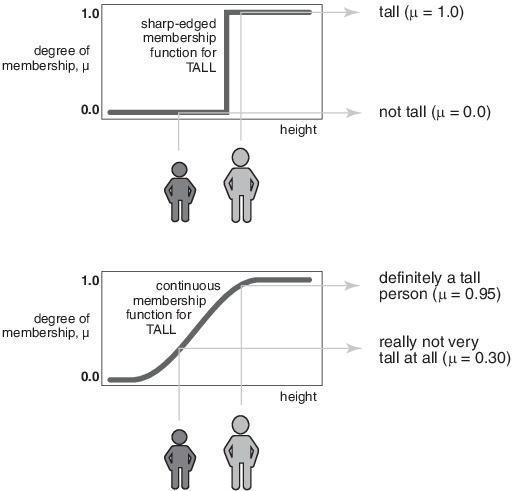
Subjective interpretations and appropriate units are built into fuzzy sets. If you say "She's tall," then the tall membership function should already take into account whether you are referring to a six-year-old or a grown woman. Similarly, the units are included in the curve since it makes no sense to say "Is she tall in inches or in meters?"
Membership Functions in Fuzzy Logic Toolbox Software
The only condition a membership function must satisfy is that its membership values must vary between 0 and 1. The function itself can be an arbitrary optimized for your desired combination of simplicity, convenience, speed, and efficiency.
A classical set might be expressed as:
A fuzzy set is an extension of a classical set. If X is the universe of discourse and its elements are denoted by x, then a fuzzy set A in X is defined as a set of ordered pairs.
µA(x) is called the membership function (or MF) of x in A. The membership function maps each element of X to a membership value between 0 and 1.
Fuzzy Logic Toolbox™ software includes 13 built-in membership function types. These functions are, in turn, built from several basic functions.
Piecewise linear functions
Gaussian distribution function
Sigmoid curve
Quadratic and cubic polynomial curves
The simplest membership functions are formed using straight lines. These straight-line membership functions have the advantage of simplicity.

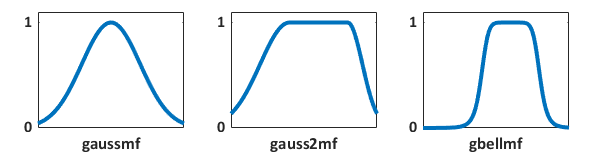
Two membership functions are derived from Gaussian
distributions: a simple Gaussian curve (gaussmf) and a two-sided composite of different Gaussian curves
(gauss2mf).
The generalized bell-shaped membership function
(gbellmf) has a similar smooth transition
between 0 and 1. It has a third parameter that you can use to adjust the
steepness of the transition from 0 to 1.
Because of their smoothness and concise notation, Gaussian and bell-shaped membership functions are popular methods for specifying fuzzy sets. Both of these curves have the advantage of being smooth and nonzero at all points.
Although the Gaussian and bell-shaped curves achieve smoothness, they are
unable to specify asymmetric membership functions, which are important in
certain applications. To do so, you can use the sigmoidal
membership function (sigmf), which is a smooth membership
function that is open to either the left or right. You can create asymmetric and
closed membership functions based on either the difference (dsigmf) or product (psigmf) of two sigmoidal functions.
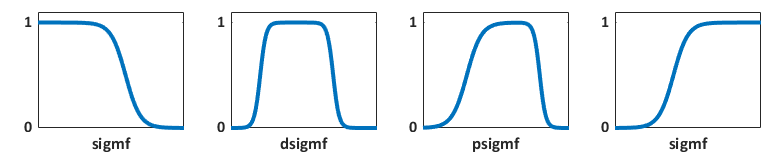
You can also create smooth membership functions using polynomial-based curves that are named for their shapes.
You can also create your own custom membership functions. For more information, see Build Fuzzy Systems Using Custom Functions.
Logical Operations
Now that you understand the fuzzy inference, you need to see how fuzzy inference connects with logical operations.
The most important thing to realize about fuzzy logical reasoning is the fact that it is a superset of standard Boolean logic. In other words, if you keep the fuzzy values at their extremes of 1 (completely true), and 0 (completely false), standard logical operations hold. As an example, consider the following standard truth tables.
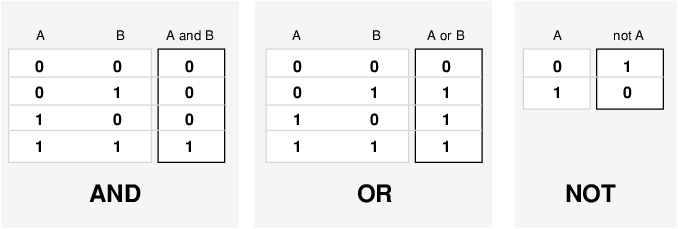
Considering that, in fuzzy logic, the truth of any statement is a matter of degree, can these truth tables be altered? The input values can be real numbers between 0 and 1. What function preserves the results of the AND truth table (for example) and also extend to all real numbers between 0 and 1?
One answer is the min operation. That is, resolve the statement A AND B, where A and B are limited to the range (0,1), by using the function min(A,B). Using the same reasoning, you can replace the OR operation with the max function, so that A OR B becomes equivalent to max(A,B). Finally, the operation NOT A becomes equivalent to the operation . The previous truth table is completely unchanged by this substitution.

Moreover, because there is a function behind the truth table rather than just the truth table itself, you can now consider values other than 1 and 0.
The next figure uses a graph to show the same information. In this figure, the truth table is converted to a plot of two fuzzy sets applied together to create one fuzzy set. The upper part of the figure displays plots corresponding to the preceding two-valued truth tables, while the lower part of the figure displays how the operations work over a continuously varying range of truth values A and B according to the fuzzy operations you have defined.
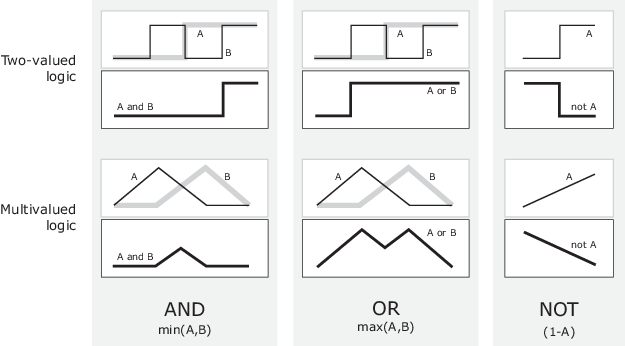
Given these three functions, you can resolve any construction using fuzzy sets and the fuzzy logical operation AND, OR, and NOT.
Additional Fuzzy Operators
In this case, you defined only one particular correspondence between two-valued and multivalued logical operations for AND, OR, and NOT. This correspondence is by no means unique.
In more general terms, you are defining what are known as the fuzzy intersection or conjunction (AND), fuzzy union or disjunction (OR), and fuzzy complement (NOT). The classical operators for these functions are: AND = min, OR = max, and NOT = additive complement. Typically, most fuzzy logic applications make use of these operations and leave it at that. In general, however, these functions are arbitrary. Fuzzy Logic Toolbox software uses the classical operator for the fuzzy complement as shown in the previous figure, but also enables you to customize the AND and OR operators.
The intersection of two fuzzy sets A and B is specified in general by a binary mapping T, which aggregates two membership functions as follows:
For example, the binary operator T may represent the multiplication of µA(x) and µB(x). These fuzzy intersection operators, which are usually referred to as T-norm (triangular norm) operators, meet the following basic requirements:
A T-norm operator is a binary mapping T(.,.) with the following properties:
Boundary —
Monotonicity — if and
Commutativity —
Associativity —
The first requirement imposes the correct generalization to crisp sets. The second requirement implies that a decrease in the membership values in A or B cannot produce an increase in the membership value in A intersection B. The third requirement indicates that the operator is indifferent to the order of the fuzzy sets to be combined. Finally, the fourth requirement allows us to take the intersection of any number of sets in any order of pair-wise groupings.
Like fuzzy intersection, the fuzzy union operator is specified in general by a binary mapping S:
For example, the binary operator S can represent the addition of µA(x) and µB(x). These fuzzy union operators, which are often referred to as T-conorm (or S-norm) operators, must satisfy the following basic requirements:
A T-conorm (or S-norm) operator is a binary mapping S(.,.) with the following properties:
Boundary —
Monotonicity — if and
Commutativity —
Associativity —
Several parameterized T-norms and dual T-conorms have been proposed in the past, such as those of Yager [11], Dubois and Prade [1], Schweizer and Sklar [8], and Sugeno [9]. Each of these provides a way to vary the gain on the function so that it can be very restrictive or very permissive.
If-Then Rules
Fuzzy sets and fuzzy operators are the subjects and verbs of fuzzy logic. These if-then rule statements are used to formulate the conditional statements that comprise fuzzy logic.
A single fuzzy if-then rule assumes the form
| If x is A, then y is B |
where A and B are linguistic values defined by fuzzy sets on the ranges (universes of discourse) X and Y, respectively. The if-part of the rule "x is A" is called the antecedent or premise, while the then-part of the rule "y is B" is called the consequent or conclusion. An example of such a rule might be
| If service is good then tip is average |
The concept good is represented as a number between 0 and 1, and so the antecedent is an interpretation that returns a single number between 0 and 1. Conversely, average is represented as a fuzzy set, and so the consequent is an assignment that assigns the entire fuzzy set B to the output variable y. In the if-then rule, the word is gets used in two entirely different ways depending on whether it appears in the antecedent or the consequent. In MATLAB® terms, this usage is the distinction between a relational test using "==" and a variable assignment using the "=" symbol. A less confusing way of writing the rule would be
| If service == good, then tip = average |
In general, the input to an if-then rule is the current value for the input variable (in this case, service) and the output is an entire fuzzy set (in this case, average). This set will later be defuzzified, assigning one value to the output. The concept of defuzzification is described in the next section.
Interpreting an if-then rule involves two steps:
Evaluation of the antecedent — Fuzzifying the inputs and applying any necessary fuzzy operators.
Application of the result to the consequent.
The second step is known as implication. For an if-then rule, the antecedent, p, implies the consequent, q. In binary logic, if p is true, then q is also true (p → q). In fuzzy logic, if p is true to some degree of membership, then q is also true to the same degree (0.5p → 0.5q). In both cases, if p is false, then the value of q is undetermined.
The antecedent of a rule can have multiple parts.
| If sky is gray and wind is strong and barometer is falling, then ... |
In this case, all parts of the antecedent are calculated simultaneously and resolved to a single number using the logical operators described in the preceding section. The consequent of a rule can also have multiple parts.
| If temperature is cold, then hot water valve is open and cold water valve is shut |
In this case, all consequents are affected equally by the result of the
antecedent. How is the consequent affected by the antecedent? The consequent
specifies a fuzzy set be assigned to the output. The implication
function then modifies that fuzzy set to the degree specified by the
antecedent. The most common ways to modify the output fuzzy set are truncation using
the min function (where the fuzzy set is truncated as shown in
the following figure) or scaling using the prod function (where
the output fuzzy set is squashed). Both are supported by the toolbox, but you use
truncation for the examples in this section.

Summary of If-Then Rules
Interpreting if-then rules is a three-part process. This process is explained in detail in the next section:
Fuzzify inputs: Resolve all fuzzy statements in the antecedent to a degree of membership between 0 and 1. If there is only one part to the antecedent, then this is the degree of support for the rule.
Apply fuzzy operator to multiple part antecedents: If there are multiple parts to the antecedent, apply fuzzy logic operators and resolve the antecedent to a single number between 0 and 1. This is the degree of support for the rule.
Apply implication method: Use the degree of support for the entire rule to shape the output fuzzy set. The consequent of a fuzzy rule assigns an entire fuzzy set to the output. This fuzzy set is represented by a membership function that is chosen to indicate the qualities of the consequent. If the antecedent is only partially true, (i.e., is assigned a value less than 1), then the output fuzzy set is truncated according to the implication method.
In general, one rule alone is not effective. Two or more rules that can play off one another are needed. The output of each rule is a fuzzy set. The output fuzzy sets for each rule are then aggregated into a single output fuzzy set. Finally the resulting set is defuzzified, or resolved to a single number. Build Fuzzy Systems Using Fuzzy Logic Designer shows how the whole process works from beginning to end for a particular type of fuzzy inference system called a Mamdani type.
References
[1] Dubois, Didier, and Henri M. Prade. Fuzzy Sets and Systems: Theory and Applications. Mathematics in Science and Engineering, v. 144. New York: Academic Press, 1980.
[2] Kaufmann, A., and Madan M. Gupta. Introduction to Fuzzy Arithmetic: Theory and Applications. Van Nostrand Reinhold Electrical/Computer Science and Engineering Series. New York, N.Y: Van Nostrand Reinhold Co, 1985.
[3] Lee, C.C. "Fuzzy Logic in Control Systems: Fuzzy Logic Controller. I." IEEE Transactions on Systems, Man, and Cybernetics 20, no. 2 (April 1990): 404–18. https://doi.org/10.1109/21.52551.
[4] Lee, C.C. "Fuzzy Logic in Control Systems: Fuzzy Logic Controller. II." IEEE Transactions on Systems, Man, and Cybernetics 20, no. 2 (April 1990): 419–35. https://doi.org/10.1109/21.52552.
[5] Mamdani, E.H., and S. Assilian. "An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller." International Journal of Man-Machine Studies 7, no. 1 (January 1975): 1–13. https://doi.org/10.1016/S0020-7373(75)80002-2.
[6] Mamdani, E.H. "Advances in the Linguistic Synthesis of Fuzzy Controllers." International Journal of Man-Machine Studies 8, no. 6 (November 1976): 669–78. https://doi.org/10.1016/S0020-7373(76)80028-4.
[7] Mamdani, E.H. ‘Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis’. IEEE Transactions on Computers C–26, no. 12 (December 1977): 1182–91. https://doi.org/10.1109/TC.1977.1674779.
[8] Schweizer, B. and A. Sklar, "Associative functions and abstract semi-groups." Publ. Math. Debrecen 10 (1963): 69–81.
[9] Sugeno, M., "Fuzzy measures and fuzzy integrals: a survey." (M.M. Gupta, G. N. Saridis, and B.R. Gaines, editors) Fuzzy Automata and Decision Processes. North-Holland, NY: 1977. 89–102.
[10] Sugeno, Michio, ed. Industrial Applications of Fuzzy Control. Amsterdam ; New York : New York, N.Y., U.S.A: North-Holland ; Sole distributors for the U.S.A. and Canada, Elsevier Science Pub. Co, 1985.
[11] Yager, Ronald R. "On a General Class of Fuzzy Connectives." Fuzzy Sets and Systems 4, no. 3 (November 1980): 235–42. https://doi.org/10.1016/0165-0114(80)90013-5.
[12] Yager, Ronald R., and Dimitar P. Filev. "Generation of Fuzzy Rules by Mountain Clustering." Journal of Intelligent and Fuzzy Systems 2, no. 3 (1994): 209–19. https://doi.org/10.3233/IFS-1994-2301.
[13] Zadeh, L.A. "Fuzzy Sets." Information and Control 8, no. 3 (June 1965): 338–53. https://doi.org/10.1016/S0019-9958(65)90241-X.
[14] Zadeh, Lotfi A. "Outline of a New Approach to the Analysis of Complex Systems and Decision Processes." IEEE Transactions on Systems, Man, and Cybernetics SMC-3, no. 1 (1973): 28–44. https://doi.org/10.1109/TSMC.1973.5408575.
[15] Zadeh, L.A. "The concept of a linguistic variable and its application to approximate reasoning. I."Information Sciences 8, no. 3 (1975): 199–249. https://doi.org/10.1016/0020-0255(75)90036-5
[16] Zadeh, L.A. "The concept of a linguistic variable and its application to approximate reasoning. II." Information Sciences 8, no. 4 (1975): 301–357. https://doi.org/10.1016/0020-0255(75)90046-8
[17] Zadeh, L.A. "The concept of a linguistic variable and its application to approximate reasoning. III." Information Sciences 9, no. 1 (1975):43–80. https://doi.org/10.1016/0020-0255(75)90017-1
[18] Zadeh, L.A. "Fuzzy Logic." Computer 21, no. 4 (April 1988): 83–93. https://doi.org/10.1109/2.53.
[19] Zadeh, L.A. "Knowledge Representation in Fuzzy Logic." IEEE Transactions on Knowledge and Data Engineering 1, no. 1 (March 1989): 89–100. https://doi.org/10.1109/69.43406.